Строительство и архитектура/ 3. Современные технологии строительства, реконструкции и реставрации

Ст-т Ведерников А.Н.; к.т.н. Кузнецова С.Г.

Пермский национальный исследовательский политехнический университет

Подбор упругой характеристики опор шарнирной цепи

Для шарнирной цепи с двумя одинаковыми упругими опорами (рис.1) подберем упругую характеристику опор «с» («с» - осадка опоры под действием единичной силы), при которой опоры ведут себя как вполне жесткие, т.е. допускают потерю устойчивости цепи с искривлением её элементов.

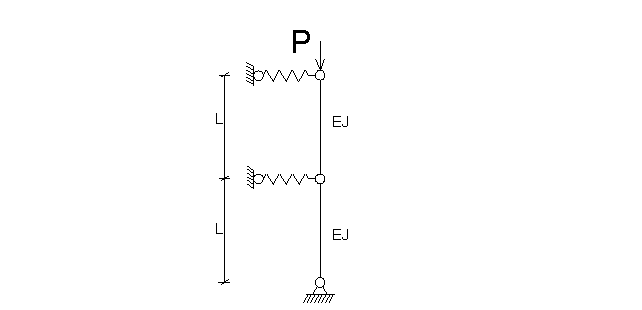
Рис.1

Используем метод перемещений. Очевидно, что степень кинематической неопределимости равна 2. Основная система метода перемещений и единичные эпюры приведены на рис. 2. Получим систему двух уравнений:

А)

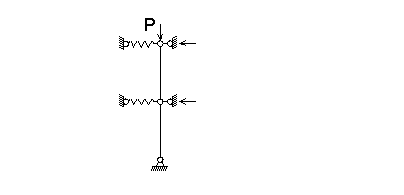
Z1=1

Z2=1

В)

Б)

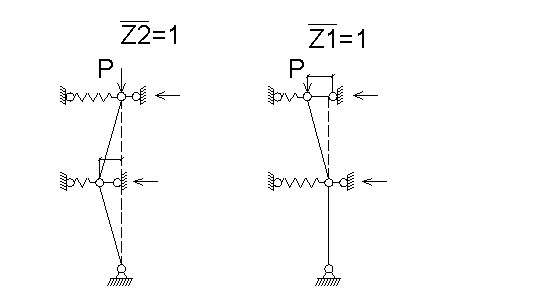
Рис. 2

Если корни уравнений равны нулю , имеем, либо отсутствие потери устойчивости, либо потерю устойчивости с искривлением её элементов без смещения опор цепи (см. рис. 3). Тогда необходимо рассматривать отдельно все звенья как шарнирно-опертые стержни, при этом .

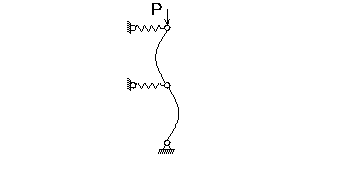
Рис. 3

Рассмотрим случай, когда корни уравнений не равны 0. Получим уравнение устойчивости, приравняв определитель полученной выше матрицы нулю: . Определим , , , рассматривая равновесие узлов первого единичного состояния (рис.4) и второго единичного состояния (рис.5)

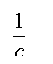
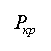
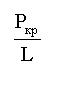
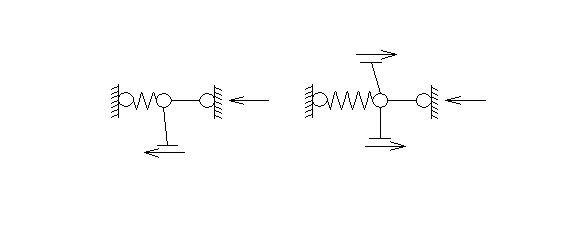
Рис. 4

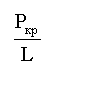
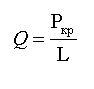
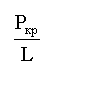
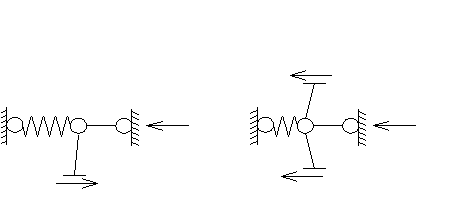
Рис. 5

Тогда уравнение устойчивости: .

Решив уравнение относительно , получим: и . Следовательно и . Откуда и . Соответствующие им формы потери устойчивости приведены на рис. 6. Выбираем первое значение, соответствующее наименьшей критической силе . Если будет больше или равно , то опоры можно считать вполне жесткими, т.к. наряду со смещением опор возможно искривление элементов. При этом .

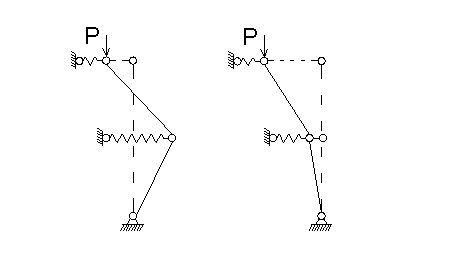
Рис. 6

Литература:

1. М.П. Сон, С.Г. Кузнецова. Строительная механика зданий и сооружений. Спецкурс: учебное пособие / М.П. Сон, С.Г. Кузнецова. – Пермь: Изд-во Пермского государственного технического университета, 2009. – 185 с.