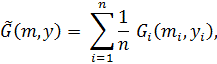BEST DECISION FOR PREVENTING COLLISIONS AT LOCAL LEVELS

Capt. Vadim Astrein, Associated Professor, MSU Admiral F.F. Ushakov,

e-mail astrein-vadim@rambler.ru

Abstract. This article deals with the task of searching for the best control decisions for preventing collisions at local elements level. Search based on optimization of multilevel hierarchical systems by predicting the ships interactions in accordance with COLREG-72.

Key words. Collision avoidance, hierarchical, multilevel systems, coordinator, interaction, compatible technology.

The classic approach to control preventing collision at sea is focused on the Collision avoidance control system (CACS) without internal activity. Such a simplified method identifying the best decision for preventing collisions at sea is inadequate. The practical application of Collision avoidance process (CAP) involves two types of control actions:

– information (meta-control) control on the intellectual information system;

– energy (power) control by using the main engine and propeller – rudder complex group.

In the modern shipping there is a urgent need for overall quality results for the carriage of goods requiring optimization, i.e. the minimum of accidents at sea and maximum yield of marine transport. These features make it possible to develop the HSPC optimization approaches to the global and local tasks of CAP’s. However, the idea of optimization requires a cautious attitude in the process of optimal modeling the HSPC. Best does not mean safe. For this opinion, there are good reasons. Take a look at some of them:

1) an optimal solution is often volatile, i.e. minor changes in the State of the vessel or the Environment could lead to significantly different choices of action/alternatives/rules.

2) optimization criteria and mathematical models of subsystems are always associated with the overall goal as the result of action to avoid collision only indirectly, i.e. more or less adequately but always close.

3) build the optimal model of interaction of subsystems allows only local optimization for subsystems with optimization criteria. If each subsystem of the HSPC will work optimally it absolutely does not mean that optimally would work and the system as a whole.

Therefore the term "optimal decision" for preventing collisions is inadequate. “The best decision” would be a solution that does not exceed a certain level of the maximum allowable value of some evaluation function of the HSPC. In this case, the use of the term: “the best decision to preventing collisions” will comply with COLREG-72 and marine professional terminology.

If there is danger of a collision of two vessels the "best decision" is achieved by coordinating effects on the main engines and rudders of both ships maneuvering in accordance with the rules of COLREG-72 to result in passing at a safe distance. Thus the task is to find a parametric conversion courses and speeds of both vessels )) which is based on information received from key local elements of every ship allows you to obtain the global coordinating effects for collision avoidance. The validity of action to prevent collision will be limited to the features of the ship itself, technological limitations, prevailing circumstances and conditions.

The general task can be formulated as follows: given a fixed values and uncontrollable factors , stochastic uncontrollable factors and fuzzy uncontrolled factors find the controlled factors belonging to the areas of their valid values which possibly could at maximum criterion in accordance with the COLREG’s Since the criterion is quantitative measure of the achievement of the HSPC goal then mathematically it is expressed in the maximum possible increase in the value criterion, i.e.

,

(1)

In fact the HSPC is a complex of hierarchical, multilevel systems. Figure 1 shows the HSPC coordinating with use of the principle of forecasting of interactions. The Global parent control system shows as the Global coordinator . Two vessels are controlled by the Local coordinators and the Subordinate local systems by first ship ( and by the second ship (.

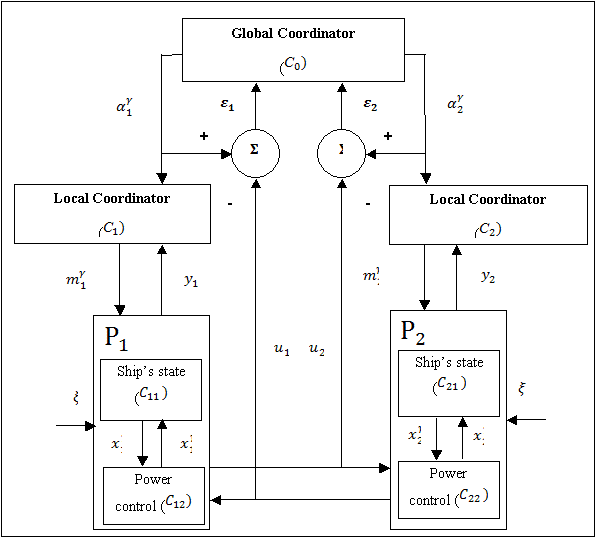
Figure 1 – Coordinating with use of the principle of forecasting of interactions

In the illustration there are the following types of signals. The first type "command" signals are ( from the Local coordinators and Environment signal connected to CAP’s ( accordingly. There are decision signals from the Subordinate local systems ) and ) from ( and (.

The role of ( is the ship control operators. The signals are belonging from them have controlling effects (outputs), while signals from the Coordinator to the Local Coordinators are called coordinating inputs. Generally the environment influences to the CAP’s and finally produces a control signal (.

Another kind of vertical signals is a transfer of feedback information signals whose task is recognition error (ε).

In order to find the best decision can be used according to the paper [1] the "principle of prediction of interactions”. Then the selected coordinating signal (γ) may be represented as:

,

(2)

where:

- predicted connecting signal;

– the actual connecting signal appears when a control action is ;

- decision by local elements ( and (.

The best decision is the task of choice )) in a feedback chain with resolving of errors . The resulting value of errors based on certain predefined parameters can be considered as transition from its original state characterized by the set of input parameters to goal state which is effected by transferring of certain information for inputs ( and (.

When searching for the best decision to preventing collisions based on the above mentioned two types of solutions there are two interrelated tasks coordination: global and local. Global task (meta control) is the task of making the best decision for preventing collisions in accordance with COLREG’s rules of maneuvering and the Local task (power control) would be the best solution to combine technical, technological, etc. tasks performed by the local elements of the vessels.

New coordinating signal can be obtained using a suitable transformation of to error (ε):

(3)

The decision on the level of local tasks will be coordinated on a global task any time whenever they coordinated on a global task (task of preventing collisions). If the global and local tasks are compatible the global goal is achieved when the Global coordinator coordinates by the power controls of the Local coordinators in relation to the global best decision task according to the formula (1) on the principles of coherence subsystems [1].

Let mark through the global task of best decision which reflects the global goal of the HSPC and specified by pairs (. Where is the goal function as per formula (4), is the power control actions and is local function of quality:

; (m) = (m, P(m)), where: operating signal; - process; – best decision; ))).

(4) (5)

In equation (5) shows the relationship between global and local tasks. In practice implementation of the decision by the formula (5) local function of quality plays a major role in CAP. Local tasks have an important influence on the ship’s actions coherence and feasibility of COLREG’s.

To assess the CAP control you can enter the quality (G) function. The Global coordinator is to maximize quality functions (G) with the simultaneous variation of power control actions CAP is a coordinated process if global quality function (G) coordinated with the local function by means of the best power control actions ((. Then for any global quality function (G) you can always find local functions , such that agreed with (G):

where: – CAP’s outputs; - power control actions; - space of control functions.

(6)

Let's look at a few examples. If you need extra reverse from full ahead to full astern sometimes such order is dangerous for the diesel engine and should be avoided. "Crash stop astern" could result the engine room in a fire and “vessel not under command”. The inability of the i - local element to define completely implementing value is due to the construction of the main engine and design of other local elements (start / reverse mechanism). Apriori value и for vessels with diesel engines has shown that the best decision for preventing collisions on local-level element (main engine) is the lack of reverse on established operating mode. Based on this condition each coordinating signal γ, γ ∈ Γ determines the tasks to be solved at the level of local elements (oil pressure, exhaust gas temperature, the temperature of the cooling water, etc.). The local best decision (speed maneuver) with the diesel engine is when an element of the main engine valid modes such that

where: - specified local goal function defined on set of ; – specified subset of ; – element of .

(7)

element (the main engine) will be called the γ-best local decision for the prevention of collisions. When for collision avoidance the steering gear is used “any alteration of course to avoid collision shall, if the circumstances of the case admit, be large” and “a succession of small alterations of course should be avoided”. Hence the best local task vessel’s steering gear control (course maneuver) is when an element of the valid rudder puts such that

where: - specified local goal function defined on set of ; – specified subset of ; – element of.

(8)

In the example the solution of the Global task for collision avoidance are such valid control actions that

(9)

where:

- best of power action;

- best power effect by the engine and steering gear respectively;

is the Cartesian product of CAP’s elements per vessel, i.e. - set of acceptable control actions by the main engine with given its limitations, - set of acceptable control actions by the steering gear bearing in mind its limitations.

In general the control permissibility of each ship has a different nature and can be called by limitations of the ship itself and the restrictions imposed by any special circumstances. The power control actions will be known as the best local control actions, i.e. power control actions which relocate the ship to a safe state in accordance with the Global goal function .

Comparing ( even in the above simplified conditions, the coherence necessary between the elements at both global and local-level coordination. The principle of prediction will execute only when the best decision is achieved through local action if the predicted actions are implemented in accordance with COLREG-72:

where: predicted input, predicted power action; best decision.

(10)

The applicability of the COLREG’s prediction principles are useless if the ships begin to violate the COLREG-72. The principles of coordination deal with this problem by introducing the force elements in the global and local levels of the HSPC. That is a necessary and sufficient condition for coordination on the basis of the cooperation principles between the ships without modifying the forecasting purposes .

Literature. 1 Mesarovic M. D. Mako, I. Tahakara “Theory of hierarchical, multilevel, systems”, Moscow, Mir, 1973.