УДК 621.01
Иманбаева Нурбиби Сайрамовна –
к.т.н. (ИМиМаш им. У.А. Джолдасбекова ), Нурмаганбетова Айман Турумовна –
к.т.н. (ИМиМаш, им. У.А. Джолдасбекова),
Сазанбаева Роза Ибраевна – к.т.н.
, доцент (КазАТК),
Аубакирова Бахыт Майнышевна - –
к.т.н. , доцент (КазАТК)
ОПТИМИЗАЦИЯ
СХЕМ ПРИВОДА МНОГОКОНТУРНОГО ГРУЗОПОДЪЕМНОГО
МЕХАНИЗМА С ЗАДАННЫМ ОТНОСИТЕЛЬНЫМ ДВИЖЕНИЕМ НЕСМЕЖНЫХ ЗВЕНЬЕВ
НА ПРИМЕРЕ
ОДНОГО ВАРИАНТА СОЕДИНЕНИЯ
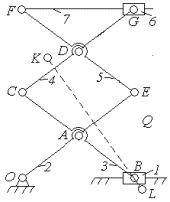
Рассмотрим задачу оптимизации схем привода
грузоподъемного механизма с заданным относительным движением несмежных звеньев
(Рисунок 1). Рассмотрены пять вариантов соединения.
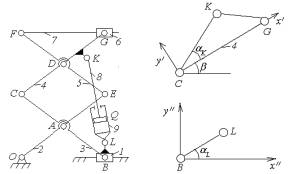Вариант соединения гидроцилиндром ползуна со звеном CG. Рассмотрим грузоподъемный механизм, представленный на
рисунке 26, а, в котором гидроцилиндр
соединяет звено 1 (ползун) со звеном 4 (CG).
Целью задачи является определение
Рисунок 1
оптимального расположения
гидроцилиндра
, при котором достигается оптимальная передача силы в
механизме, т.е. определение переменных 
(рисунок 1, б), а также допустимых значений 
, при которых достигается минимальное значение усилия в
гидроцилиндре 
[1,2].
Пусть 
- локальные координаты шарнира К относительно системы координат 
(рисунок 1), жестко связанной со звеном CG (ось
направлена вдоль
звена CG); 
- локальные координаты шарнира L относительно системы координат 
(рисунок 1), жестко связанной с ползуном, движущейся
поступательно. Тогда абсолютные координаты кинематических пар К и L вычисляются
по формулам
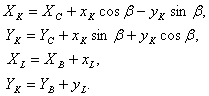(1)
Тогда длина гидроцилиндра в заданном положении
определяется по формуле
(2)
Будем добиваться минимума усилия в гидроцилиндре, для
чего необходимо минимизировать критерий, отражающий передачу усилия
. (3)
Значение 
будем вычислять по
приближенной формуле
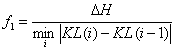, (4)
где
.
При этом будем также учитывать конструктивное
ограничение (дополнительное условие)
, (5)
где
- коэффициент запаса. Будем добиваться увеличения 
.
Значения варьируемых переменных будем менять с помощью
генератора 
-последовательностей, равномерно распределенных в заданной
области поиска
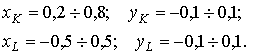(6)
Для этого использована методика точек Соболя [3]. Если
ограничить значения главного критерия 
, то получим фрагмент разброса значений 
, показанный на рисунке 2.
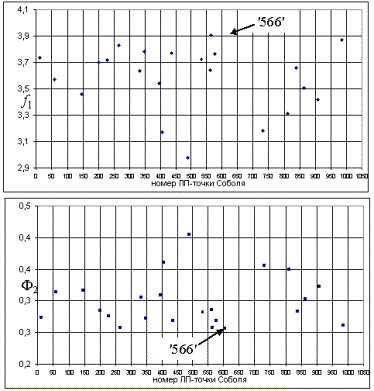
Рисунок 2 - Разброс значений 
и 
в зависимости от номеров точек Соболя
При рассмотрении 
точек Соболя получены
22 механизма, удовлетворяющие условиям 
и 
.
Так, точке Соболя с номером ‘566’ соответствуют
значения варьируемых параметров 
.
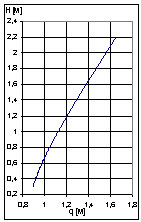
Кинематическая схема механизма, соответствующего точке ‘566’ показана на рисунке 3, а, а на рисунке 28, б показан график зависимости 
. Как мы видим, график близок к линейному.
|
|
|
|
а) |
б) |
|
Рисунок 3 - Кинематическая схема грузоподъемного механизма (А=’566’) (а) и график зависимости |
|
Максимальное значение 
=12.252кН (1250 кгС) оказалось в 3.8 раз меньше, чем в
исходной нижнеприводной схеме. В
верхнем положении 
=6.861кН (700 кгС).
Однако при предварительных расчетах таблицы испытаний
уменьшение значения 
приводило к ухудшению
конструктивного ограничения, связанного с расположением конца 
штока гидроцилиндра. Радиус-вектор точки 
определяется по
формуле
(7)
В полученных вариантах решений значения ограничения 
оказывались больше
значения 0.3. Поэтому при последующем поиске с уточненными границами
(8)
мы
добивались 
. Разброс значений варьируемых параметров для полученных
механизмов показан на рисунке 4. При рассмотрении 
точек Соболя получены
12 механизмов, удовлетворяющих заданным условиям.
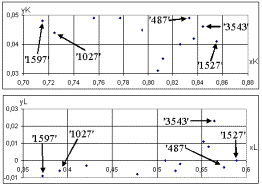
Рисунок 4 - Разброс значений
варьируемых параметров
Усеченный график разброса значений главного критерия 
и дополнительного
условия 
, показанное в зависимости от номеров точек Соболя,
представлены на рисунке 5.
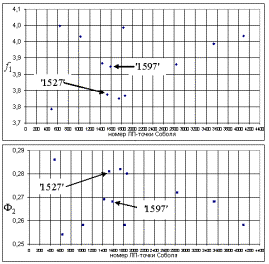
Рисунок 5 - Разброс значений 
и 
в зависимости от
номеров точек Соболя
В таблице 1 приведены значения варьируемых параметров
для отобранных 12 механизмов.
Таблица
3
|
A |
|
|
|
|
|
|
487 |
0.833 |
0.049 |
0.575 |
-0.004 |
3.743 |
|
635 |
0.808 |
0.031 |
0.521 |
-0.006 |
3.998 |
|
1027 |
0.725 |
0.044 |
0.391 |
-0.006 |
3.966 |
|
1435 |
0.795 |
0.045 |
0.509 |
0 |
3.884 |
|
1527 |
0.855 |
0.041 |
0.589 |
0 |
3.788 |
|
1597 |
0.715 |
0.048 |
0.372 |
-0.009 |
3.873 |
|
1747 |
0.756 |
0.049 |
0.421 |
-0.003 |
3.776 |
|
1831 |
0.826 |
0.04 |
0.558 |
0.008 |
3.994 |
|
1867 |
0.777 |
0.049 |
0.478 |
-0.008 |
3.784 |
|
2839 |
0.837 |
0.042 |
0.552 |
0.011 |
3.88 |
|
3543 |
0.844 |
0.046 |
0.564 |
0.023 |
3.943 |
|
4091 |
0.812 |
0.035 |
0.526 |
-0.002 |
3.967 |
Из полученных 12 механизмов отобраны механизмы с
номерами точек Соболя ‘1527’ и ’1597’. Кинематические схемы этих механизмов
представлены на рисунке 31.
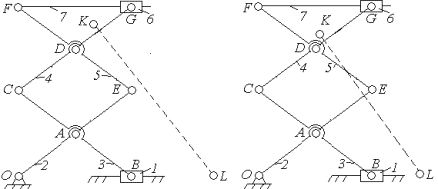
а) б)
Рисунок 31 - Кинематические схемы грузоподъемных
механизмов, соответствующие точкам Соболя
А=’1527’(а) и A=’1597’(б)
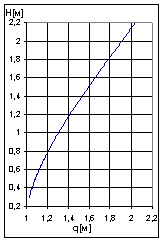
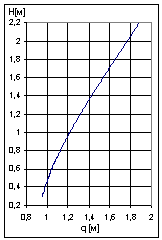
Графики зависимости 
, где 
для этих механизмов
указаны на рисунке 32.
|
A= |
A= |
||||
|
а) |
б) |
||||
|
Рисунок 32 - Графики зависимости |
|||||
Уравновешивающая сила в нижнем положении в механизме А=1527 будет равна 
=12.41кН (1266.38 кгС), а в верхнем положении 
= 4.68кН (477.76 кгС).
Уравновешивающая сила в нижнем положении в механизме А=1597 будет равна 
=12.58кН (1283.19 кгС), а в верхнем положении 
= 5.23кН (534.07 Н).
Сравнительный анализ результатов пяти вариантов схем
соединения показывает, что передачу силы удается улучшить от 2 до 4.5 раза: в
исходной схеме максимальное усилие в гидроцилиндре равно 47.02кН. При
использовании привода с качающимся гидроцилиндром в традиционных конструкциях
соединяются смежные звенья (в таблице 4 – 2-я строка). Однако в существующих
конструкциях передача усилия также нерациональная и достигает 46.36кН. Нам
удалось снизить это значение до 19.6кН. Однако возможности этой схемы, как мы
показали, достаточно ограничены.
Принимая во внимание вышеизложенное, а также то, что в верхнем
положении конструкции платформ типа «Нюрнбергские ножницы» имеют консольную
конфигурацию и низкую устойчивость, а также имеют конструктивно сложные
поступательные кинематические пары, в дальнейшем будем рассматривать
шарнирно-рычажные схемы грузоподъемного механизма.
ЛИТЕРАТУРА:
1.
Кожевников С.Н.
Основания структурного синтеза механизмов. Киев, 1979. -321с.
2. Joldasbekov U.A.,
Baigunchekov Zh.Zh. and Ibraev S.M. (1999): Kinematics
and Kinetostatics of Multi-Degree of Freedom Mechanisms of High Classes with
Given Relative Motions of Moveable Links. Proc. Tenth World Congress on the Theory of Machines and Mechanisms
of IFToMM, Oulu, Finland, 20-24 June,
1999, pp.592-596.
3. Джолдасбеков У.А. Основы кинематического и
динамического анализа механизмов высоких классов с относительным законом
движения входного звена. – Изв. АН КазССР: сер. физ. –мат., 1988, №5. с.80-83.