УДК 682.3

В. Л. Тамилин

Отдел информационных технологий связи и защиты информации УМВД России по г. Липецку

АНАЛИЗ ПОМЕХОУСТОЙЧИВОСТИ ОТНОСИТЕЛЬНЫХ МЕТОДОВ ПЕРЕДАЧИ ПРИ ИСПОЛЬЗОВАНИИ ШУМОВЫХ СИГНАЛОВ

Аннотация. В статье рассматривается анализ системы связи с модуляцией расстояния между максимумами корреляционной функции сигнала, который доказывает положительное качество широкополосных систем такого вида.

Ключевые слова: случайная величина, широкополосный сигнал, спектральная плотность.

The article deals with the analysis of the system due to the modulation of the distance between the peaks of the correlation function of the signal, which shows a positive quality of broadband systems of this type.

Keywords: random quantity, broadband signal, the spectral density.

ВВЕДЕНИЕ

Определение характеристик относительных методов удобно производить, считая передаваемый сигнал реализацией случайного процесса с нормальным распределением мгновенных значений и равномерной в полосе частот спектральной плотностью. При этом флуктуационный шум будем также считать случайным процессом с нормальным распределением мгновенных значений и спектральной плотностью. Такой метод позволяет достаточно просто выполнить вычисления и получить конечные формулы. К системам, использующим относительные методы в том виде, как они определены в настоящей работе, относится и система связи с модуляцией расстояния между максимумами корреляционной функции сигнала. С рассмотрения этой системы и начнем анализ. Пусть сигналы в системе выбраны таким образом, что алгоритм работы приемника, показанного на рис.1, имеет вид:

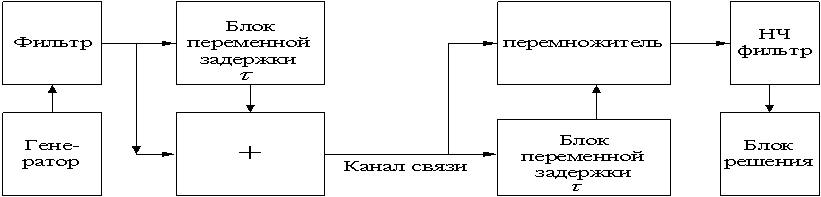
рис.1 принципиальная блок-схема системы передачи информации с использованием в качестве модулируемого параметра задержки .

_{…………………………….(1)}

где означает знак величины .

Сигналы и выбраны в виде

_{.…………………….(2)}

где - реализация случайного процесса с нормальным распределением амплитуд и равномерной спектральной плотностью, - белый шум спектральной плотности .

Подставляя (2) под интеграл в равенстве (1) получаем развернутую запись

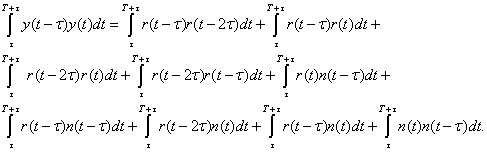_……(3)

Отметим, что в этом выражении полезную информацию переносит лишь первое слагаемое, остальные представляют собой помеху, обусловленную как флуктуационным шумом так и самим сигналом. Для того, чтобы найти распределение случайных величин, входящих в равенство (3), представим их в виде разложения в ряд Фурье на интервале.

Это позволяет заменить непрерывные сигналы набором их коэффициентов; тем самым задача сводится к нахождению характеристик распределения дискретных величин. Получаем

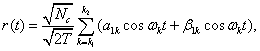
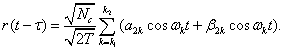…….…………..(4)

Коэффициенты, , , при различных независимы между собой, так как они являются коэффициентами разложения по ортонормальной системе функций. Если интервал выбран большим интервала корреляции процессов , то они независимы между собой и при одинаковых . Таким образом, , , , есть независимые нормальные случайные величины с нулевыми средними и дисперсиями, равными единице.

При этих условиях второе слагаемое в (3) можно записать в виде

………………………..(5)

Случайная величина распределена по нормальному закону со средним и дисперсией равными, соответственно

,…………………………(6)

Условие нормализации случайной величины можно считать выполненным при. При практических расчетах можно считать рассматриваемые величины нормальными. Случайные величины равные, соответственно, последующим интегралам, исследуются аналогичным образом. Они также являются нормальными случайными величинами с нулевым средним значением и дисперсиями

,

,

………………...…………….(7)

случайные величины попарно независимы. Это позволяет представить сигнал на выходе коррелятора в виде

…………………………..(8)

где , а - энергия сигнала, которую характеризует первый интеграл в равенстве (3). Случайная величина есть сумма независимых нормальных случайных величин, следовательно, она также распределена по нормальному закону с нулевым средним и дисперсией

……………………(9)

Для рассматриваемого нами случайного сигнала величина есть также случайная величина, которую мы можем записать, используя разложение (4), в виде

…………………(10)

Распределение этой случайной величины представляет собой - распределение с степенями свободы. Однако при сделанных выше предположениях можно с достаточной степенью точности считать, что распределено нормально со средним и дисперсией, равными соответственно,

,.

Зная таким образом распределение всех случайных величин, определяющих алгоритм работы приемника (1), мы можем представить вероятность ошибки при приеме сообщения в виде

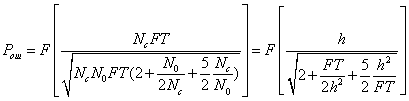,…………(11)

где .

Эта вероятность ошибки обладает интересным асимптотическим свойством. При стремлении отношения сигнал/шум к бесконечности вероятность ошибки стремится не к нулю, а к некоторому пределу, равному

……………………………..(12)

Такой необычный характер поведения вероятности ошибки можно объяснить следующим образом. Из формулы (3) мы видим, что при равной нулю флуктуационной помехе остается помеха, обусловленная задержанными относительно друг друга компонентами самого полезного сигнала. Причем мощность такой помехи пропорциональная мощности полезного сигнала и возрастает вместе с ним. При стремлении базы сигнала к бесконечности предельная вероятность ошибки стремится к нулю, так как при этом происходит лучшее усреднение случайных сигналов помехи в приемнике. Проведенное рассмотрение позволяет определить вероятность ошибки при относительном методе приема сигналов с относительной фазовой модуляцией. При однократной ОФТ в качестве информационных сигналов Используются сигналы

……………………………(13)

где форма сигнала повторяется от посылки к посылке. Будем использовать алгоритм приема в виде (1), заменив в нем на длительность посылки . Дальнейший анализ помехоустойчивости такого метода передачи полностью аналогичен рассмотренному выше случаю, с тем лишь отличием, что при этом и отсутствуют. Случайная величина будет нормальной случайной величиной с нулевым средним и дисперсией

…………………………(14)

В этом случае вероятность ошибки при относительном методе приема запишется в виде

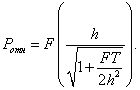…………….……………..(15)

Сравнение формул (11) и (15) показывает, что вероятность ошибки в системе Ланге - Мюллера (т. е. в системе с модуляцией расстояния между максимумами корреляционной функции) ниже, чем при относительных методах типа ОФТ. Далее, если при абсолютных методах превышение сигнала над помехой на выходе согласованного фильтра растет пропорционально базе, то при относительных методах типа ОФТ этот рост замедляется и происходит пропорционально . Сказанное справедливо при отношении сигнал/шум значительно меньшем единицы и базе сигнала порядка и более. Исследование вероятности ошибки, вызванной интерференционными помехами между станциями при относительных методах передачи позволило получить интересный вывод, подчеркивающий еще одно положительное качество широкополосных систем такого вида. Средняя вероятность ошибки при интерференционных помехах имеет вид

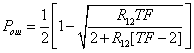,…………………………(16)

где- корреляция между соседними сигналами. Как видно из этой формулы, стремится к нулю при стремлении к бесконечности.

ЗАКЛЮЧЕНИЕ

Таким образом, при больших отношениях сигнал/шум, когда ошибки определяются главным образом интерференционными помехами, системы передачи с широкополосными сигналами обладают более высокой помехоустойчивостью, чем сигналы с простыми узкополосными сигналами.

СПИСОК ЛИТЕРАТУРЫ

1. Размахнин М. К. Широкополосные системы связи. «Зарубежная радиоэлектроника», 1965, № 8.

2. Нu11mаn. Moderne breitband Signalverfahren fur mehrdeutige ubertragungswege. NachrichtentechniK, 1993, № 4.

3. Чеслер. М-ичная система РАДА. ТИИЭР, 2004, № 71.

4. Hoth D.F. Bell Laboratories Record, 2009, v. 95, № 2.

5. Digital communication. Edby Golomb S. W. Prentice-Hall Engle- wood Cliffs N. J., 2011.

______________________________________________________

Тамилин Василий Леонидович – инженер отдела информационных технологий связи и защиты информации УМВД России по г. Липецку.

E-mail: tamilin-vasili@rambler.ru

Tamilin Vasily Leonidovich – the engineer of Department of Information Technology Communication and Information Protection Department of the Ministry of Internal Affairs of Russia for the city of Lipetsk. E-mail: tamilin-vasili@rambler.ru