Колчанова В.А., Ларкина А.С.

Национальный исследовательский Томский политехнический университет, Россия

Катушка индуктивности в цепи импульсного напряжения

Для уменьшения затрат на ревизию трансформаторов предлагается исследовать обмотки трансформаторов при подключении импульсного напряжения. Длина импульса – теста составляет 400-500 нс.

На отдельностоящую катушку высоковольтной обмотки физического макета трансформатора от генератора "Нанотест" (рис. 1) прикладывался одиночный импульс. По характеру полученной осциллограммы на выходе возможен вывод о характере повреждений обмотки трансформатора или их отсутствии. Для этих целей была создана математическая модель обмотки трансформатора.

Прямоугольной импульс (рис. 1) может быть представлен рядом Фурье. Причём 32 гармоники даёт достаточно полное совпадение, остальные гармоники больше 32 можно отбросить. Пунктиром показана восстановленная форма импульса после разложения в ряд Фурье, сплошной линией – форма исходного импульса. На рисунке справа – амплитудно частотный спектр.

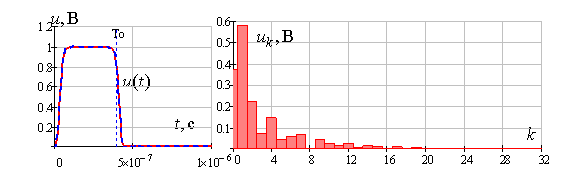
Рис. 1

В соответствии с принципом суперпозиции (наложения) расчёт можно вести для каждой гармоники отдельно. Причём с учётом того, что обычная индуктивная катушка при достаточно высоких частотах представляет собой линию с распределенными параметрами. Поэтому в схеме замещения должны присутствовать что кроме индуктивностей межвитковые емкости и емкости на корпус прибора (на землю). Так как с ростом гармоник частота увеличивается, то ток через емкости могут во много раз превышать токи через витки катушки. В этом случае вся катушка в целом будет оказывать прохождению переменного тока емкостное, а не индуктивное сопротивление (количественные изменения перешли в качественные), что обязательно должно быть учтено при составлении модели. Схема замещения одного витка катушки индуктивности представлена на рисунке 2.

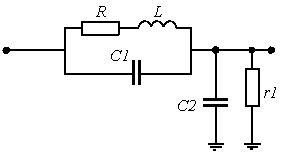
Рис. 2

Расчёт одного витка удобно вести методом переменных состояния, в качестве которых принимаем величины однозначно определяющие состояние цепи, т.е. подчиняющиеся законам коммутации – ток индуктивности; – напряжения на ёмкостях С1 и С2 соответственно. Тогда уравнение переменных состояния:

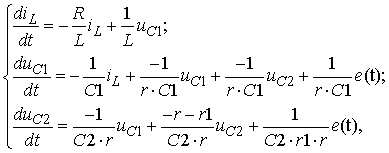
где – сопротивление в цепи генератора (внутреннее сопротивления источника прямоугольных импульсов 75 Ом).

Параметры цепи замещения для каждого витка определялись с учётом скин-эффекта. Расчётные индуктивности для разных частот определялись на основе расчёта магнитного поля в среде Matlab. Величины ёмкостей определялись на основе расчёта электростатического поля. Т. о. параметры схемы замещения: ; ; ; до ; до для разных гармоник.

Аналогичный расчёт был проведён в среде Simulink Matlab, совпадение расчётных кривых говорит об адекватности полученных результатов. Для моделирования катушки как цепи с распределёнными параметрами создана модель в среде Simulink Matlab, к которой можно варьировать величину и форму входного импульса, параметры схемы замещения, с помощью диалоговых окон подсхем (рис.3).

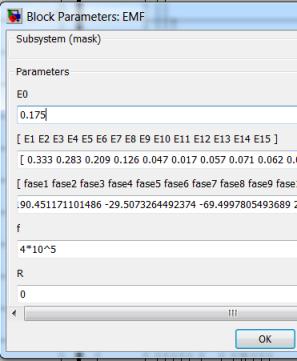
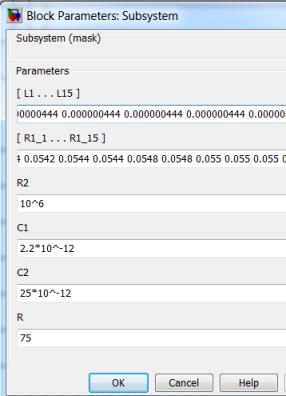
Рис. 3

Форма напряжения на катушке, полученная на построенной модели полностью совпала с эксперименальной осциллограммой, следовательно модель можно использовать для моделирования дефектов обмоток, формировать эталонные сигналы при различных повреждениях исследуемого оборудования.

Литература:

1. Теоретические основы электротехники. Электрические цепи : учебник / Л. А. Бессонов. — 11-е изд., испр. и доп. –М. : Гардарики, 2006. — 701 с.