Економічні науки/ 8. Математичні методи в економіці

Скрильник І.І., Замашка М.В.

Полтавський національний технічний університет, Україна

Застосування методу Четверикова до прогнозування прибутку Качанівського ГПЗ ПАТ «Укрнафта»

Прогнозування економічних показників підприємства на майбутнє, зокрема прибутку, є однією із актуальних задач. Існує ряд класичних методів, що базуються на апараті математичної статистики, серед яких виділяють метод Четверикова.

Постановка задачі. На основі статистичних даних за 2007 – 2011 роки (табл. 1) розробити прогнозну модель прибутку Качанівського ГПЗ ПАТ «Укрнафта». Для визначення тренда заданого часового ряду використати метод Четверикова, виконати аналіз якості отриманої прогнозної моделі: оцінити її адекватність і точність.

Таблиця 1

Статистичні дані прибутку підприємства за 2007 – 2011 роки

Рік	Квартал	Прибуток, млн.грн.	Рік	Квартал	Прибуток, млн.грн.
2007	1	5060,0	2008	1	1050,0
	2	3420,0		2	2990,0
	3	3190,0		3	4350,0
	4	3700,0		4	3990,0
2009	1	3231,0	20010	1	9547,7
	2	6831,0		2	9349,0
	3	6951,0		3	9625,0
	4	7120,0		4	12790,0
2011	1	13005,0	2012	1	прогноз
	2	14205,0		2
	3	17705,0		3
	4	16105,0		4

Розв’язання задачі. В основі методу відомого радянського вченого Миколи Сергійовича Четверикова (спеціаліста в соціально-економічній та математичній статистиці) лежить розчленування адитивної моделі ряду динаміки на компоненти. З цього приводу він зазначав: «розчленуванню підлягає динаміка, але не саме явище, яка приймає нероздільну участь у всьому складному русі».

За даним методом для виділення компонент заданого тренд-сезонного ряду використовують ітераційні методи фільтрації, основна ідея яких полягає у багатократному застосуванні ковзної середньої та одночасному оцінюванні сезонної хвилі на кожному кроці. Алгоритм методу можна описати наступними кроками.

Крок 1. Вихідний ряд вирівнюємо методом ковзної середньої. Не вирівняні значення на початку та у кінці ряду відкидаємо. Отримуємо попереднє оцінювання тренду та обчислюємо відхилення вихідного ряду від вирівняного

(1)

Крок 2. Для кожного року обчислюємо середньоквадратичне відхилення

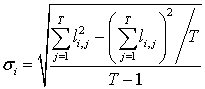(2)

та отримані відхилення нормуємо

. (3)

Крок 3. За нормованими відхиленнями обчислюємо попередню сезонну хвилю

, (4)

де – кількість років.

Крок 4. Отримуємо перше оцінювання тренду

. (5)

Крок 5. Отриманий тренд згладжуємо ковзною середньою за 5 точками та отримуємо нову оцінку тренда . Щоб не загубити значення на початку та у кінці ряду, їх згладжують за 5 точками.

Крок 6. Обчислюємо нові відхилення вихідного ряду від тренда

, (6)

Для отримання відхилень знову виконуємо кроки 2 та 3 і отримуємо остаточну середню сезонну хвилю .

Крок 7. Обчислюємо залишкову компоненту

(7)

та визначаємо – коефіцієнт напруженості сезонної хвилі:

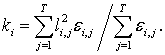(8)

За допомогою коефіцієнта напруженості k_i обчислюємо остаточні значення сезонної компоненти часового ряду

. (9)

З метою прогнозування прибутку Качанівського газопереробного заводу «Укрнафта» на перший квартал 2012 р. на основі статистичних даних за 2007 – 2011 роки (табл. 1) було розкладено ряд динаміки на складові компоненти та зроблено їх аналіз.

Практична реалізація методу виділення компонент ряду. Розрахунки проводилися за наведеним вище алгоритмом. Було визначено рівні тренда , отримано оцінку тренда (рис. 1).

Рис. 1. Графік емпіричних даних, згладженого ряду та трендів

У результаті розрахунків було отримано остаточну середню сезонну хвилю , обчислено залишкову компоненту (рис. 2), визначено – коефіцієнт напруженості сезонної хвилі (рис. 3), а також визначено остаточну сезонну компоненту (рис. 4).

Рис. 2. Графік залишкової компоненти

Рис. 3. Графік коефіцієнтів сезонних хвиль

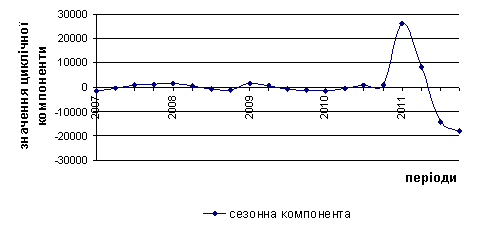
Рис. 4. Графік сезонної компоненти

Отже, за допомогою методу Четверикова було виділено компоненти заданого часового ряду: тренд, циклічність, сезонність, залишкову компоненту.

Перевірка адекватності виділених трендів. Після аналізу даних перевірено адекватність моделі. Трендова модель вважається адекватною, якщо залишкова компонента задовольняє таким вимогам і вони повинні виконуватися одночасно:

- рівність нулю математичного сподівання;

- випадковість виникнення окремих відхилень від тренда;

- наявність або відсутність автокореляції у відхиленні моделі;

- відповідність ряду залишків нормальному закону розподілення.

Автори дослідили виділені тренди на адекватність. Отримано такі результати.

Таблиця 2

Дослідження адекватності тренда

Тренд	1 вимога	2 вимога	3 вимога	4 вимога
	;	;	; ;	; ;
Висновок	,
	виконується	виконується	виконується	виконується

Прогнозні значення було отримано методом екстраполяції даних рівнів часового ряду . Прибуток підприємства, за даною моделлю, на перший квартал 2012 року складатиме 15505,86 млн. грн.

Проведено верифікацію побудованої моделі. Фактичний прибуток підприємства у першому кварталі 2012 р. становив 17530,6 млн. грн., тобто розрахунковий результат відрізняється від фактичних даних на 2024,748 млн. грн., тобто похибка становить 11,6% .

Таблиця 3

Дослідження адекватності тренда

Тренд	1 вимога	2 вимога	3 вимога	4 вимога
	;	;	; ;	; ;
Висновок	,		, залишки автокорельовані
	виконується	виконується	не виконується	виконується

Висновок. Отже, на основі тренда заданого ряду динаміки доцільно визначати прогнозні значення. Визначено, що точність прогнозу кожного рівня ряду становить 98,89%.

Література:

1. Афанасьев В.Н. Анализ временных рядов и прогнозирование: Учебник. / В.Н. Афанасьев, М.М. Юзбашев. – М.: Финансы и статистика, 2001 – 200 с.

2. Агафонова Н.Ю. Анализ временных рядов. Учебное пособие / Н.Ю. Агафонова. – Саратов, 2010 – 27 с.

3. Горелова В.Л. Основы прогнозирования систем: Учеб. пособ. для инж.-экон. спец. вузов / В.Л. Горелова, Е.Н. Мельникова – М.: Высш. шк., 1986. – 287 с.: ил.

4. Толбатов Ю.А. Економетрика: Підручник для студентів екон. Спеціальн. вищ. навч. закл. / Ю.А.Толбатов – К.; Четверта хвиля, 1997. – С. 39-73, С.143-153.

5. Скрильник І.І. Прогнозування соціально-економічних процесів : навчальний посібник / І.І. Скрильник, О.Г. Климко. – Полтава: ПолтНТУ, 2012. – 227 с.