География и геология/ Гидрология и водные ресурсы

Магистр Койшибаева Г.Д., Абдирова И.М.

Таразский государственный университет им. М. Х. Дулати

СОВЕРШЕННЫЙ ГИДРАВЛИЧЕСКИЙ ПРЫЖОК И ЕГО ОСНОВНОЕ УРАВНЕНИЕ

Скачкообразное возрастание глубины потока при переходе из бурного состояния (h₁ <h_к) в спокойное (h₂ >h_к), сопровождаемое интенсивными макротурбулентными пульсациями скоростей и давлений, называют гидравлическим прыжком. Область прыжка ограничена живыми сечениями до прыжка ω₁ и после прыжка ω₂ соответственно с глубинами h₁ и h₂  (рис. 1). Глубины до и после прыжка называются сопряженными глубинами. Разность h₂ –h₁   представляет собой высоту прыжка, а l_п – длину прыжка.

Рисунок 1 Схема гидравлического прыжка

Если (h₂/ h₁)≥2, то прыжок считается совершенным.

Исследования гидравлического прыжка начались еще в XV веке и продолжаются до сих пор. Единственная задача, имеющая чисто теоретическое решение - задача определения высотных размеров гидравлического прыжка в горизонтальном гладком призматическом прямоугольном русле.

Из рассмотрения именно этого частного случая отталкивались многие ученые. Так, например, в прошлом веке Ж.Б.Беланже было сформулировано определение гидравлического прыжка как уникальное физическое явление. Позже Ж. Буссинеск рассмотрев это явление, определил область возникновения прыжка и ввел такое понятие как критическая глубина. Опираясь на труды этих ученых, уже позже было выведено основное уравнение гидравлического прыжка. [1]

(1)

Введя новые обозначения

; (2)

Из (1) имеем: (3)

Уравнение (3) показывает, что для сопряженных глубин прыжковые функции имеют одну и ту же величину. Следовательно, можно найти одну сопряженную глубину, зная другую глубину прыжка.

Для русла любого сечения  при заданном расходе Q можно построить график прыжковой функции (рис.1).

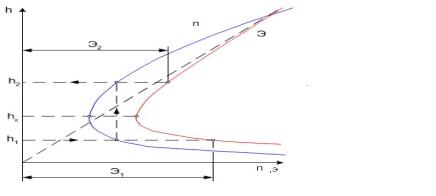
Рисунок 2 График прыжковой функции

Из уравнения (1) нельзя получить таких величин, как длину прыжка, потери энергии и другие параметры.

Длина гидравлического прыжка определяется экспериментально, и обычно ее выражают в долях от высоты гидравлического прыжка, сопряженных глубин и кинетичности потока.

Профессором Таразского государственного университета Абдурамановым А.А. было выведено уравнение совершенного гидравлического прыжка, из которого можно получить длину гидравлического прыжка, а также потери энергии.

Совершенный гидравлический прыжок является неравномерным движением, это видно из уравнения А.А. Абдураманова [2]

(4)

где l_п- длина прыжка; - средняя площадь поперечных сечений начала и конца прыжка; I - гидравлический уклон потока в прыжке; i - уклон дна русла между началом и концом прыжка.

Умножая обе части на получим:

(5)

При этом (I –i)≠0

Из последнего уравнения мы видим, что под действием разности внешних сил [ ] масса жидкости () в прыжке движется с ускорением .

Это есть второй закон Ньютона, т.е.

Пользуясь уравнением А.А. Абдураманова можно определить гидравлические и геометрические параметры совершенного гидравлического прыжка.

Так длину прыжка мы находим по формуле:

(6)

здесь , тогда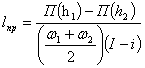

Потери напора в совершенном гидравлическом прыжке можно найти используя уравнение Бернулли для прямоугольного русла:

(7)

В этом уравнении , тогда

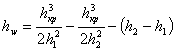
Подставив в уравнение (10) получим:

(8)

Уравнение А.А. Абдураманова позволит нам обобщить все особенности движения воды в совершенном гидравлическом прыжке, что не удавалось до сих пор.

Далее в процессе постановки экспериментальных работ мы сможем установить гидравлические и геометрические параметры совершенного гидравлического прыжка, а также построить график прыжковой функции, согласно уравнению А.А. Абдураманова.

Литература:

1. П.Г. Киселев. Гидравлика основы механики жидкости.- М.: Энергия, 1980.-360 с.

2. Чугаев Р.Р. Гидравлика. – М.: Энергия, 1977.

3. А.А. Абдураманов. Гидравлика. – Тараз, 2010, «Сеным» - 472с.