СОВРЕМЕННЫЕ ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ/2. Вычислительная техника и программирование

Золотухина Ирина Андреевна, магистрант

Костанайский государственный университет имени А. Байтурсынова, Казахстан.

Методы и алгоритмы обучения нейронных сетей.

Аннотация: в данной статье проведен анализ нейронных сетей, почему они настолько актуальны, рассмотрим разновидности нейросетевых алгоритмов, области применения сетей.

Ключевые слова: нейрон, перцептрон, метод Розенблатта, метод Хебба, ошибка обобщения, ошибка обучения, алгоритм обучения.

Нейронные сети (или искусственные нейронные сети) – это одно из интереснейших направлений исследований в области искусственного интеллекта, основанное на моделировании и воспроизведении нервной системы человека. Особенно ученых интересуют такие процессы как: способность нервной системы обучаться, исправлять ошибки, принимать решения, что должно позволить смоделировать работу человеческого мозга.

Искусственные нейронные сети обучаются путем анализа положительных и отрицательных воздействий. Они состоят из нейронов, которые названы так по аналогии с биологическим прототипом.

Впервые предложили модель искусственного нейрона американские ученые Уоррен Маккалок (Warren McCulloch) и его ученик Уолтер Питт (Walter Pitts) в 1943 году.

В зависимости от функций, выполняемых нейронами в сети, можно выделить три их типа[1]:

· входные нейроны, на которые подается вектор, кодирующий входное воздействие или образ внешней среды; в них обычно не осуществляется вычислительных процедур;

·промежуточные нейроны, составляющие основу нейронных сетей, преобразования в которых выполняются по выражениям (1) и (1.1);

· выходные нейроны, выходные значения которых представляют выходы нейронной сети; преобразования в них осуществляются также по выражениям (1) и (1.1).

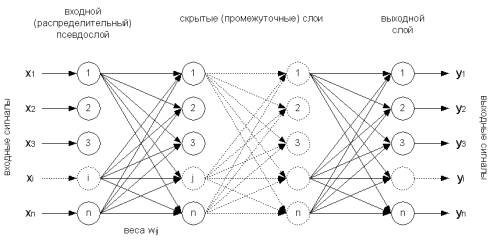
Рис 1. Структура формальной нейронной сети

(1)

y = f(s) (1.1)

где

· w_i, – вес (weight) синапса, i = 1...n;

· b – значение смещения;

· s – результат суммирования;

· x, – компонент входного вектора (входной сигнал),

· x_i = 1...n;

· у – выходной сигнал нейрона;

· n – число входов нейрона;

· f – нелинейное преобразование (функция активации).

На входной сигнал (s) нелинейный преобразователь отвечает выходным сигналом f(s), который представляет собой выход у нейрона.

Преимущества нейросетевого подхода при решении задач информационных технологий в отличие от других (например, архитектуры фон Неймана):

· параллелизм обработки информации;

· единый и эффективный принцип обучения;

· надежность функционирования;

· способность решать неформализованные задачи.

Применение и проблемы, решаемые искусственными нейронными сетями

Искусственные нейронные сети нашли своё применение в различных областях техники. Дальнейшее повышение производительности компьютеров все в большей мере связывают с развитием именно этих сетей, в частности, с нейрокомпьютерами, основу которых составляет искусственная нейронная сеть.

Круг задач, решаемых нейронными сетями:

· распознавания образов;

· распознавания и синтеза речи;

· распознавания аэрокосмических изображений;

· обработки сигналов при наличии больших шумов;

· прогнозирования;

· оптимизации;

· прогнозирования котировки ценных бумаг и курса валют;

· предупреждения мошенничества с кредитными карточками;

· игра на бирже;

· фильтрация спама;

· оценки стоимости недвижимости;

· оценки финансового состояния предприятий и риска невозврата кредитов;

· обработки радиолокационных сигналов;

· системы безопасности и видеонаблюдения;

· контроля движения на скоростных автомагистралях и железных дорогах;

· диагностики в медицине;

· управление сложными объектами;

· добычи знаний из больших объемов данных в бизнесе, финансах и научных исследованиях;

· управления в реальном времени и это далеко не всё.

Обучение

Под обучением понимается, повышение производительности системы путем анализа входных данных. Причем обучение проходит по определённым правилам.

Существуют два основных подхода к обучению: «с учителем» и «без учителя» (самообучение). При обучении с учителем нейронная сеть располагает правильными ответами (выходами сети) на каждый входной пример. Вместе они называются обучающей парой. Веса настраиваются так, чтобы сеть производила ответы как можно более близкие к известным правильным ответам, минимизировалась ошибка. Векторы обучающего множества предъявляются последовательно, вычисляются ошибки и веса подстраиваются для каждого вектора до тех пор, пока ошибка по всему обучающему массиву не достигнет приемлемого уровня. Обучение без учителя не требует знания правильных ответов на каждый пример обучающей выборки. В этом случае раскрывается внутренняя структура данных или зависимость между образцами в системе данных, что позволяет распределить образцы по категориям[2].

Обучение с учителем

На вход искусственной нейронной сети подается множество входных нейронов X — входной вектор для обучаемой нейронной сети.

Определим функцию ошибки E. Обычно это средняя квадратичная ошибка,

,

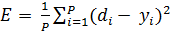где

· P — количество обработанных нейронной сетью примеров;

· y_i —выход;

· d_i — желаемый (идеальный) выход нейронной сети.

Процедура обучения нейронной сети сводится к процедуре коррекции весов связей. Целью процедуры коррекции весов есть минимизация функции ошибки E.

Общая схема обучения с учителем:

1 Перед началом обучения весовые коэффициенты устанавливаются некоторым образом, на пример — случайно.

2 На первом этапе на вход в определенном порядке подаются учебные примеры. На каждой итерации вычисляется ошибка для учебного примера E_L(ошибка обучения) и по определенному алгоритму производится коррекция весов. Целью процедуры коррекции весов есть минимизация ошибки E_L.

3 На втором этапе обучения производится проверка правильности работы. На вход в определенном порядке подаются контрольные примеры. На каждой итерации вычисляется ошибка для контрольного примера E_G (ошибка обобщения - ошибка, которую обучаемая модель показывает на примерах, не участвовавших в процессе обучения). Если результат неудовлетворительный то, производится модификация множества учебных примеров и повторение цикла обучения.

Если после нескольких итераций алгоритма обучения ошибка обучения E_L падает почти до нуля, в то время как ошибка обобщения E_G в начале спадает а затем начинает расти, то это признак эффекта переобучения. В этом случае обучение необходимо прекратить.

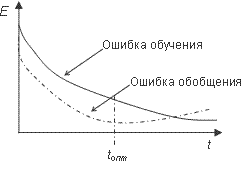
Рис 2. Эффект переобучения

На основе этого алгоритма строится обучение нейронной сети методом Розенблатта.

Метод Розенблатта

Данный метод был предложен Ф.Розенблаттом в 60-х годах XX века Для нейронной сети, названной персептрон (perceptron). Персептрон имеет пороговую функцию активации, его схема представлена на рис.1.

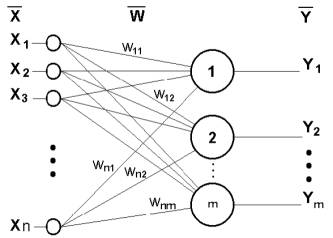
Рис 3. Однослойный персептрон

Процедуру обучения Розенблатта для однослойного персептрона можно представить так:

,

где

· x_i — i-тый вход нейронной сети;

· d_j — желаемый (идеальный) j-тый выход нейронной сети;

· a — коэффициент (скорость обучения) 0< a ≤1

Весовые коэффициенты меняются только в том случае, если реальное выходное значение не совпадает идеальным выходным значением. Ниже приведено описание алгоритма обучения персептрона.

1. Полагаем все веса равными нулю.

2. Проводим цикл предъявления примеров. Для каждого примера выполняется следующая процедура.

2.1. Если сеть выдала правильный ответ, то переходим к шагу 2.4.

2.2. Если на выходе персептрона ожидалась единица, а был получен ноль, то веса связей, по которым прошел единичный сигнал, уменьшаем на единицу.

2.3. Если на выходе персептрона ожидался ноль, а была получена единица, то веса связей, по которым прошел единичный сигнал, увеличиваем на единицу.

2.4. Переходим к следующему примеру. Если достигнут конец обучающего множества, то переходим к шагу 3, иначе возвращаемся на шаг 2.1.

1.

2.

3. Если в ходе выполнения второго шага алгоритма хоть один раз выполнялся шаг 2.2 или 2.3 и не произошло зацикливания, то переходим к шагу 2. В противном случае обучение завершено.

В этом алгоритме не предусмотрен механизм отслеживания зацикливания обучения. Этот механизм можно реализовывать по-разному. Наиболее экономный в смысле использования дополнительной памяти имеет следующий вид.

4. k=1; m=0. Запоминаем веса связей.

5. После цикла предъявлений образов сравниваем веса связей с запомненными. Если текущие веса совпали с запомненными, то произошло зацикливание. В противном случае переходим к шагу 3.

6. m=m+1. Если m<k, то переходим ко второму шагу.

7. k=2k; m=0. Запоминаем веса связей и переходим к шагу 2.

Поскольку длина цикла конечна, то при достаточно большом k зацикливание будет обнаружено.

Обучение без учителя.

Главная черта, делающая обучение без учителя привлекательным, – это его "самостоятельность". Процесс обучения, как и в случае обучения с учителем, заключается в подстраивании весов синапсов. Некоторые алгоритмы, правда, изменяют и структуру сети, то есть количество нейронов и их взаимосвязи, но такие преобразования правильнее назвать более широким термином – самоорганизацией, и в рамках данной статьи они рассматриваться не будут. Очевидно, что подстройка синапсов может проводиться только на основании информации, доступной в нейроне, то есть его состояния и уже имеющихся весовых коэффициентов. Исходя из этого соображения и, что более важно, по аналогии с известными принципами самоорганизации нервных клеток, построены алгоритмы обучения Хебба.

По существу Хэбб предположил, что синаптическое соединение двух нейронов усиливается, если оба эти нейрона возбуждены. Это можно представить как усиление синапса в соответствии с корреляцией уровней возбужденных нейронов, соединяемых данным синапсом. По этой причине алгоритм обучения Хэбба иногда называется корреляционным алгоритмом.

Идея алгоритма выражается следующим равенством:

,

где

· y_i^(n-1) – выходное значение нейрона i слоя (n-1),

· y_j⁽ⁿ⁾ – выходное значение нейрона j слоя n;

· w_ij(t) и w_ij(t-1) – весовой коэффициент синапса, соединяющего эти нейроны, на итерациях t и t-1 соответственно;

· a – коэффициент скорости обучения.

Здесь и далее, для общности, под n подразумевается произвольный слой сети. При обучении по данному методу усиливаются связи между возбужденными нейронами.

Существует также и дифференциальный метод обучения Хебба, представленный формулой

, (2)

здесь y_i^(n-1)(t) и y_i^(n-1)(t-1) – выходное значение нейрона i слоя n-1 соответственно на итерациях t и t-1;

y_j⁽ⁿ⁾(t) и y_j⁽ⁿ⁾(t-1) – то же самое для нейрона j слоя n.

Как видно из формулы (2), сильнее всего обучаются синапсы, соединяющие те нейроны, выходы которых наиболее динамично изменились в сторону увеличения.

Полный алгоритм обучения с применением вышеприведенных формул будет выглядеть так:

1. На стадии инициализации всем весовым коэффициентам присваиваются небольшие случайные значения.

2. На входы сети подается входной образ, и сигналы возбуждения распространяются по всем слоям согласно принципам классических прямопоточных (feedforward) сетей, то есть для каждого нейрона рассчитывается взвешенная сумма его входов, к которой затем применяется активационная (передаточная) функция нейрона, в результате чего получается его выходное значение y_i⁽ⁿ⁾, i=0...M_i-1, где M_i – число нейронов в слое i; n=0...N-1, а N – число слоев в сети.

3. На основании полученных выходных значений нейронов по формуле (1) или (2) производится изменение весовых коэффициентов.

4. Цикл с шага 2, пока выходные значения сети не застабилизируются с заданной точностью. Применение этого нового способа определения завершения обучения, отличного от использовавшегося для сети обратного распространения, обусловлено тем, что подстраиваемые значения синапсов фактически не ограничены.

На втором шаге цикла попеременно предъявляются все образы из входного набора.

Следует отметить, что вид откликов на каждый класс входных образов не известен заранее и будет представлять собой произвольное сочетание состояний нейронов выходного слоя, обусловленное случайным распределением весов на стадии инициализации. Вместе с тем, сеть способна обобщать схожие образы, относя их к одному классу. Тестирование обученной сети позволяет определить топологию классов в выходном слое. Для приведения откликов обученной сети к удобному представлению можно дополнить сеть одним слоем, который, например, по алгоритму обучения однослойного перцептрона необходимо заставить отображать выходные реакции сети в требуемые образы[3].

Необходимо отметить, что обучение без учителя гораздо более чувствительно к выбору оптимальных параметров, нежели обучение с учителем. Во-первых, его качество сильно зависит от начальных величин синапсов. Во-вторых, обучение критично к выбору радиуса обучения и скорости его изменения. И наконец, разумеется, очень важен характер изменения собственно коэффициента обучения. В связи с этим пользователю, скорее всего, потребуется провести предварительную работу по подбору оптимальных параметров обучения сети.

Несмотря на некоторые сложности реализации, алгоритмы обучения без учителя находят обширное и успешное применение. По сути дела, по алгоритму обучения без учителя функционируют и наиболее сложные из известных на сегодняшний день искусственные нейронные сети – когнитрон и неокогнитрон. Они очень хорошо справлялись с задачей распознавания изображений подвергнутых смещениям в позиции, зашумлению, искажению формы. Тем не менее, неокогнитрон не справлялся с задачей, когда изображение было повернуто на некоторый угол.

В заключение можно сказать, что в настоящее время ученые занимаются исследованием искусственных нейронных сетей, устойчивости тех или иных конфигураций, однако далеко не все задачи могут быть решены нейронными сетями. Несмотря на то, что искусственный нейрон является моделью биологического нейрона, он далеко не совершенен и требует значительной работы, новых открытий в области искусственного интеллекта. Нейронные сети не в состоянии обучаться, как человек. Тем не менее, на основе вышеизложенного материала можно создать реально действующие системы для распознавания образов, сжатия информации, автоматизированного управления, экспертных оценок и много другого.

Литература:

1. В.В.Круглов, В.В.Борисов «Искусственные нейронные сети», 2002 год.

2. Rumelhart D. E., Hinton G. E., Williams R. D. Learning internal reprentation by error propagation in parallel distributed processing. – Cambrige: MA: MIT Press, 1986. – 91 p.

3. http://www.scorcher.ru/neuro/science/neurocomp/mem52.php