Математика/1.Дифференциальные и интегральные уравнения

Далбина С. , студентка 4 курса , Даулетбаева Ж., старший преподаватель

Костанайский государственный университет, Казахстан

Приложения преобразования Фурье к уравнениям математической физики

ФУРЬЕ (Fourier) Жан Батист Жозеф (1768 -1830), французский математик и физик, научный советник Наполеона в Египте с 1798 по 1801 г. Его исследования в области математического анализа теплового потока привели к разработке метода, известного сейчас под названием метода Фурье. По этому методу сложные периодически изменяющиеся функции разлагаются на суммы волн, и последующий анализ производится уже с учетом этих волн, которые легче поддаются анализу, чем первоначальные функции.

Основной областью занятий Фурье была математическая физика. В 1807 и

1811 он представил Парижской Академии Наук свои первые открытия по теории распространении тепла в твёрдом теле, а в 1822 опубликовал известную работу «Аналитическая теория теплоты», сыгравшую большую роль в последующей истории математики.

Преобразования являются линейными операторами и, с соответствующей нормализацией, унитарными (свойство, известное как теорема Парсеваля, или, в более общем случае, как теорема Планшереля, или, в наиболее общем, как дуализм Понтрягина).

Поэтому, целью статьи является – исследовать понятия математической физики тесно связанные с преобразованием Фурье, а так же их применение к решению уравнений математической физики[1].

Многие физические приборы - это операторы (преобразователи). На вход приборов подаются сигналы функции , , … - они входят в область определения оператора. На выходе получаем соответственно функции , , …. Например, усилители можно рассматривать как операторы, преобразующие напряжение переменного тока , подаваемого на вход, в напряжение переменного тока, получаемого на выходе. Преобразователь называется линейным, если он удовлетворяет следующим условиям:

если преобразуется в , то ( - любая действительная константа, ) преобразуется в ;

если преобразуется в , а - в , то преобразуется в .

Если для преобразователя выполняются указанные выше условия, то говорят, что для преобразователя выполняется принцип суперпозиции. Дополнительно предполагаем, что функция преобразуется в функцию , то есть, что установившееся гармоническое колебание с частотой преобразуется в установившееся гармоническое колебание с той же частотой . Причем, , где , - главное значение аргумента (). называется спектральной характеристикой преобразователя, которая означает, что гармонические колебания с различными частотами прибор преобразует по-разному. Гармоническое колебание преобразуется в гармоническое колебание

Модуль спектральной характеристики , то есть называется частотной характеристикой преобразователя. Она показывает, во сколько раз изменяется амплитуда гармонического колебания с данной частотой . А называется фазовой характеристикой преобразователя. Она показывает изменение фазы. Имеем прямую задачу[2].

Дано: 1) физический прибор - линейный преобразователь,

- его спектральная характеристика;

-функция на выходе (абсолютно интегрируемая на числовой прямой и кусочно-гладкая на любом отрезке числовой прямой).

Найти: - преобразованную функцию на выходе.

Находим преобразование Фурье функции .

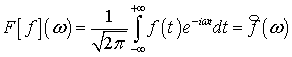, (1)

По формуле обращения преобразования Фурье находим

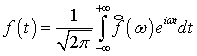, (2)

Интеграл правой части равенства можно рассматривать как «сумму» бесконечно большого числа бесконечно малых гармонических колебаний

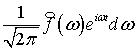, (3)

Преобразователем гармонические колебания (3) преобразуются в гармонические колебания

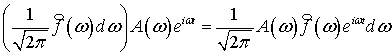,(4)

«Сумма» колебаний (3) преобразуется в «сумму» колебаний (4). Тогда функция , определяемая соотношением (2), преобразуется в функцию , определяемую соотношением

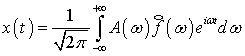, (5)

Литература:

1 Преобразование Фурье: учебно-методическое пособие / сост.: Н.П. Семенчук, Н.Н. Сендер; Брест. Гос. Ун-т имени А.С. Пушкина. - Брест: БрГУ, 2011. - 42 с.

2 Владимиров В.С. Уравнение математической физики – Москва «Наука», 1981.