Сулейменов З.И. к.ф.-н.,доцент,

Наукенова М.Д., Касымбекова М.Т.,- магистр

Казахский национальный технический университет им. К.И. Сатпаева

РАСПРЕДЕЛЕНИЯ СВЯЗАННЫЕ С НОРМАЛЬНЫМ ЗАКОНОМ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН

Центральная предельная теорема теории вероятностей (теорема Ляпунова)доказывает, что если варьирование случайной величины происходит под воздействием большого числа независимых факторов подчиненных каким угодно законам распределения, причем влияние каждого из них незначительно по сравнению с совокупным воздействием других факторов, то распределение случайной величины подчиняется нормальному закону [1,2,3].

Известные распределения случайных величин получены разными методами, например показательное распределение как решение дифференциального уравнения, распределение Стьюдента получены эмпирическим путем и др.

В данной статье мы предлагаем получить известные и другие распределения на основе единого подхода, принимая за основу нормальный закон распределения случайных величин.

Известно, что если случайная величина имеет плотность распределения вероятностей , то плотности распределения вероятностей, для величины определяется следующей формулой:

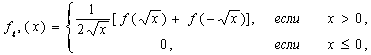(1)

а для величины :

(2)

Если случайная величина имеет нормальное распределение с параметрами , то будем использовать сокращенное обозначение

Теорема 1. Если случайные величины независимы и , то величина имеет распределение Эрланга порядка .

Доказательство. Действительно, величины имеют гамма – распределение с параметрами 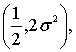которые получаются по формуле (1), а величины имеют экспоненциальные распределения с параметрами которые получаються путем композиции гамма – распределении. Тогда, на основании теоремы 3.1. доказонной в [2] стр.145 имеем, что случайная величина имеет распределение Эрланга порядка с плотностью

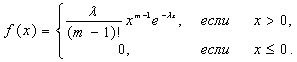(3)

что и требовалось доказать.

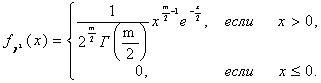Плотность вероятности случайной переменной где имеет вид [1,2,3,4]:

(4)

Распределение (4) называют распределением хи – квадрат с степенями свободы.

Теорема 2. Если случайные величины независимы и , то имеет распределение Релея, а имеет распределение Максвелла.

Действительно, плотность распределения вероятностей случайной величины имеет вид:

тогда по формуле (2):

(5)

Распределение (5) называют распределением Релея.

Аналогично находим: 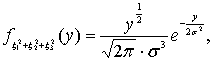(6)

Распределение (6) называют распределением Максвелла.

Теорема 3. Если случайные величины и - независимы и

, то случайная величина имеет распределение Коши с параметрами ,где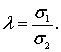

В несколько более общей форме эта теорема доказывается в [1].

Плотность вероятности распределения Коши имеет вид:

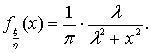(7)

Теорема 4. Если случайные величины и - независимы и , то случайные величины и имеют распределения:

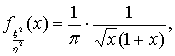(8)

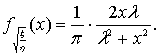(9)

формулы (8) и (9) получаются из формул (1), (2) и (7).

Теорема 5. Если случайные величины и независимы и

, то случайная величина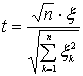

имеет распределение Стьюдента со степенями свободы и с плотностью:

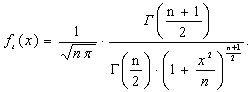(10)

доказательство теоремы 5 даны в [1,4].

Теорема 6. Если случайные величины независимы и , то плотность распределения вероятностей случайной величины 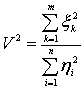имеет вид:

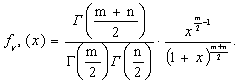(11)

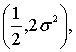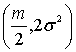Доказательство. и имеют гамма – распределения с параметрами тогда согласно теореме 3.2 в [ ] стр.146, и имеют гамма распределения с параметрами и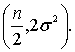

Пользуясь формулы распределения частного от деления двух случайных величин с гамма распределением, получаем формулу (11).Распределение (11) называют распределением Фишера – Снедекора или распределением.

Теорема 7. Если случайные величины независимы и а то случайная величина имеет следующую плотность распределения вероятнотей:

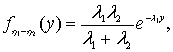(12)

где

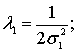
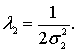
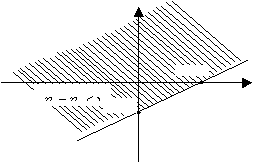
Доказательство.

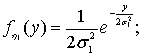
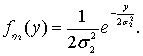
Cобытие означает, что точка попадает в заштрихованную область на рис.1.

Тогда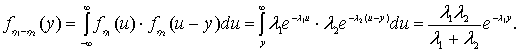

Таким образом, все рассмотренные в данной работе плотности распределения вероятностей случайной величины получены на основе нормально распределенных случайных величин.Путем выполнения определенных операции над нормально распределенными случайными величинами можно получить выражения для еще неизвестных плотностей распределения вероятностей.

Литература

1.Гнеденко Б.В. Курс теории вероятностей. М.:Наука, 1988-448с.

2.Математическая статистика: Учеб.для вузов/ В.Б. Горяинов, И.В.Павлов, Г.М. Цветков и др.-М.: Изд-во МГТУ им.Н.Э.Баумана, 2001.-424с.

3.Гурский Е.И. Теория вероятностей с элементами математической статистики.М.:”высшая школа”, 1971.-328с.

4.Сулейменов З.И.Ықтималдықтар теориясы және математикалық статистика элементтері.- Алматы: ҚазҰТУ, 2014.-275б.