Математика/5. Математическое моделирование

к.ф.-м.н. доц. В.И. Евсеев

Казанский (Приволжский) федеральный университет, Казань, Россия,

кафедра прикладной информатики

УДК 681.32 1 - vladislaw.evseev@yandex.ru, т.89047610772

СТРУКТУРИРОВАНИЕ ТЕРНАРНЫХ ЛОГИЧЕСКИХ СХЕМ

Тернарные операции являются обобщением бинарных операций на случай, когда заданы три исходных высказывания: X,Y, Z. Так как каждое высказывание определяет покрытие универсума, то в этом случае общее покрытие будет трёхслойным. Здесь строится последовательность бинарных операций, которая называется композицией, то есть, тернарная операция является композиций бинарных операций. При этом одна из бинарных операций, которая выполняется первой, называется внутренней, а вторая – внешней. Символически можно обозначить внутреннюю бинарную операцию символом “ ”, а внешнюю – символом “□”или “◊”.

Так как последовательность выполнения двух бинарных операций может быть различной, то можно рассмотреть два вида схем тернарных операций: а) первой выполняется внутренняя композиция

(1)

а затем – внешняя операция

. (2)

Результатом является тернарная операция

(3)

б) внутренняя бинарная операция выполняется второй,

в этом случае

. (4)

Эту операцию удобно представить в виде композиции, если положить для внутренней бинарной операции:

(5)

Тогда получаем:

(6)

Для построения таблиц истинности тернарных операций также будем использовать матричный метод, который основан на применении матриц Карно. При этом сначала каждая внутренняя бинарная операция записывается в виде рабочих блоков, затем также записывается внешняя бинарная операция, а после первый результат подставляется в полученное выражение и вычисляется окончательный вид рабочих блоков символьного массива. В таблицах Карно обычно крайним считается высказывание, характеризующее внешнюю операцию. Однако при построении сравнительных таблиц высказывания расставляются по договоренности, чтобы иметь возможность сравнивать результаты.

Рассмотрим схемы для обоих видов тернарных операций, а затем приведём некоторые наиболее существенные для дальнейшего изложения примеры.

а) Если первой выполняется внутренняя бинарная операция

то её матрица истинности может быть записана в виде:

Y X	0	1
0
1

Поэтому символьный массив записывается через рабочие блоки:

(7)

Для внешней бинарной операции получаем соответствующую таблицу истинности:

Z M	0	1
0
1

Значит, для внешней бинарной операции получаем формулу рабочих блоков:

(8)

Предварительно вычисляем значение : (9)

Теперь выражения из формул (7) и (.9) подставляем в формулу для внешней операции и находим окончательное выражение для всей тернарной операции.

Символьный массив для тернарных операций первого типа может быть записан в виде таблицы:

Q ( 1 тип )

На основе символьного массива строится совокупность рабочих блоков тернарной операции первого типа. В дальнейшем мы будем опускать символ конъюнкции и записывать выражения в виде стандартного произведения.

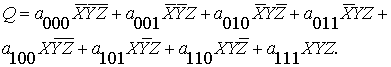(10)

Здесь приняты обозначения

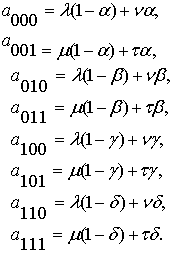(11)

Значит, матрица функции истинности по схеме Карно может быть записана в виде:

Z	Y X	0	1
0	0
0	1
1	0
1	1

Аналогично получаются результаты и для второго вида тернарных операций. Этот случай может быть записан в виде:

(12)

где

Эти бинарные операции расписываются стандартным образом. Кроме матричных таблиц Карно в логике применяется графическое изображение специального вида, которое называется полем Канта. Для тернарной операции первого типа поле Канта имеет вид:

Y X	0		1
0
		Z
1

В этом поле проводится штриховка (заливка) рабочих блоков. Рабочие поля имеют шифр, соответствующий набору значений функции истинности тернарной операции.

Обычно при решении конкретных задач в схеме поля Канта не указывают наборы значений входящих высказываний, чтобы более наглядно изобразить саму заливку полей, соответствующих рабочим блокам.

Аналогичная схема поля Канта получается и для второго типа тернарных операций (с учётом перестановки высказываний).

Эту структуру можно представить таблицей:

Z Y	0		1
0
		X
1

Теперь рассмотрим конкретные примеры тернарных операций различных типов, применяя к ним общую схему исследования с помощью символьных массивов, характеризующих рабочие блоки операции и таблиц Карно, как структурной модели операции.

а) Операции первого типа, содержащие как основные, так и взаимные, бинарные операции.

Сразу заметим, что такого вида операций бесчисленное множество. Поэтому мы остановимся лишь на некоторых примерах.

1а) Тернарные композиции, содержащие только один рабочий блок.

Их особенностью является присутствие в матрице Карно единственного значения «1».

1.1.1. Q=(X&Y)&Z. (13)

Рассматриваем внутреннюю и внешнюю бинарные операции

M=X&Y, Q=M&Z (14)

Для них получаем структуры четырех блоков:

Y X
	0	0
	0	1

Z M		Z
	0	0
	0	1

Следовательно, для всей бинарной операции получаем такой вид таблицы Карно:

Z	Y X	0	1
0	0	0	0
0	1	0	0
1	0	0	0
1	1	0	1

Поле Канта в этом примере имеет вид:

Y X	0		1
0
		Z
1

Естественно, что при этом:

(15)

1.1.2. Пусть задана формула

Q =(X&Y)\Z . (16)

В этой задаче используются взаимные функции: поляризация, и конъюнкция, для которых ранее были найдены матрицы истинности и рабочие блоки. Поэтому мы не будем приводить полностью всех вычислений по правилам четырёх блоков, которые довольно просты. Последовательность действий при составлении и анализе тернарных операций нами приведена в предыдущем примере и является универсальной. Поэтому ограничимся краткой сводкой результатов. Не приводя всех вычислений, сразу запишем результат в виде матрицы Карно:

Z	Y X	0	1
0	0	0	0
0	1	1	0
1	0	0	0
1	1	0	0

Значит, в этом примере также только один рабочий блок

.

Функция истинности здесь принимает вид:

(17)

Отметим, что этот результат показывает довольно слабую логическую силу построенной формулы. Изобразим и поле Канта для этой задачи:

Y X	0		1
0
		Z
1

2а) Тернарные операции, содержащие два рабочих блока.

1.1.3. (18)

Здесь для внутренней операции получаем матрицу

Y X
	1	0
	0	1

а для внешней операции имеем результат Q=M&Z (19)

Z M		Z
	0	0
	0	1

В итоге получаем формулу рабочих блоков

(20)

Теперь составим матрицу Карно для всей операции:

Z	Y X	0	1
0	0	0	0
0	1	1	0
1	0	0	0
1	1	0	1

Не останавливаясь на выражении функции истинности, изобразим для рассмотренного примера поле Канта, имеющее только два рабочих (залитых) поля.

Схема Канта имеет вид:

Y X	0		1
0
		Z
1

Сравнивая рассмотренные примеры, видим, что поле Канта в первом случае является частью поля Канта во втором случае. Таким образом получаем импликацию:

б) Операции второго типа.

Рассмотрим примеры тернарных композиций, содержащих три или четыре рабочих блока.

1б) Формула содержит три рабочих блока.

1.2.1. (21)

Здесь внутренняя бинарная операция – импликация,

Для нее формула рабочих блоков

При этом отрицание имеет один рабочий блок

Внешняя операция является конъюнкцией

Поэтому получаем

(22)

Теперь записываем матрицу Карно для этой операции:

Z	Y X	0	1
0	0	0	0
0	1	1	0
1	0	0	0
1	1	1	1

Мы не будем приводить явный вид функции истинности, предоставив читателю самостоятельно закончить задачу.

Здесь поле Канта имеет вид:

Y X	0		1
0
		Z
1

1.2.2. Путь матрица Карно содержит четыре рабочих блока:

Получаем для внутренней операции ( нильюнкции)

А для внешней операции – эквиваленции

(23)

Таким образом, получаем матрицу Карно для всей операции:

Z	Y X	0	1
0	0	0	1
0	1	1	0
1	0	1	1
1	1	0	0

Соответствующее поле Канта имеет схему:

Y X	0		1
0
		Z
1

Рекомендуем читателям самостоятельно рассмотреть различные сочетания внутренних и внешних бинарных операций для получения навыков работы с тернарными операциями.

в) Заметим, что тернарными по своей сути являются и так называемые сложные бинарные операции, в частности, «усечённая» дважды бинарная операция, которую в общем случае можно представить в виде формулы:

(24)

где в скобках указаны внутренние бинарные операции, а вне скобок находится внешняя бинарная операция.

Для таких операций сначала рассматриваются обе внутренние операции и находятся их рабочие блоки, затем строятся отрицания этих бинарных композиций, а все результаты подставляются в выражение внешней бинарной операции.

Заметим, что для сложных тернарных операций, какими являются дважды бинарные операции, применяется лексикографическая последовательность высказываний (X,Y,Z).

Приведём два примера таких композиций.

3.1.1. Рассмотрим дважды бинарную операцию

(25)

Для нее получаем вид внутренних операций:

(26)

(27)

Внешняя операция – дизъюнкция – имеет следующие рабочие блоки:

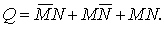(28)

Подставляя в эту формулу выражения для внутренних операций и их отрицаний, получим:

(29)

Таким образом, в данной тернарной операции имеется всего три рабочих блока и пять нерабочих.

Значит, матрица Карно для этой тернарной операции имеет вид:

Z	Y X	0	1
0	0	0	0
0	1	1	1
1	0	0	0
1	1	1	0

Для рассматриваемого примера получаем поле Каната:

Y X	0		1
0
		Z
1

3.1.2. Рассмотрим ещё один подобный пример:

(30)

Строим, как и в первом случае, формулы внутренних бинарных

операций и их отрицаний

(31)

Внешняя операция – конъюнкция, она приводит к результату:

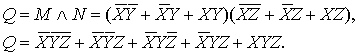(32)

Строим матрицу Карно для этой тернарной операции:

Z	Y X	0	1
0	0	1	1
0	1	0	0
1	0	1	1
1	1	0	1

Для этого случая также построим поле Канта:

Y X	0		1
0
		Z
1

Отметим, что если обозначить результат примера 3.1.1. через , а результат примера 3.1.2. через , то получаем:

(33)

Естественно, что при этом заливка полей Канта оказывается дополнительной.

Поэтому эквиваленция этих формул является противоречием.

Примечание 1.Традиционно, доказательство этого факта занимает целую страницу с весьма сложными выкладками. Это ещё раз демонстрирует эффективность матричных методов, применяемых нами.

Примечание 2. Иногда рассматриваются так называемые «обратные задачи», когда исходно определена только таблица истинности (в традиционных случаях – это линейная таблица), и по указанным в ней значениям функции истинности предлагается построить вид самой тернарной операции. Оказывается, что в этом случае представление в виде композиции двух бинарных операций становится затруднительным (даже порой неразрешимым).

При этом тернарная операция имеет таблицу:

n	0	1	2	3	4	5	6	7
X	0	1	0	1	0	1	0	1
Y	0	0	1	0	0	0	1	1
Z	0	0	0	0	1	1	1	1
Q	a	b	c	d	e	f	g	h

Сначала мы рекомендуем построить поле Канта по заданным значениям рабочих блоков, а затем записать выражение для совокупности рабочих блоков и функцию истинности этой операции.

ЛИТЕРАТУРА

1. Ю.Л.Ершов, Е.А. Палютин. Математическая логика. СПб. 2005.

2. Дж.Шенфилд. Математическая логика. М.«Наука». 1975

3. Евсеев В.И. Логика. Монография. «ТАРИ». Казань. 2001.