Математика/5. Математическое моделирование

к.ф.-м.н. доц. В.И. Евсеев

Казанский (Приволжский) федеральный университет, Казань, Россия,

кафедра прикладной информатики

УДК 681.32 1 - vladislaw.evseev@yandex.ru, т.89047610772

СИММЕТРИЧНЫЕ МНОГОСЛОЙНЫЕ ОПЕРАЦИИ

1. Тернарная логическая операция называется симметричной, если её результат не зависит от последовательности входящих в неё трёх исходных высказываний. Такие операции легко получить из общей формулы тернарной операции путём наложения условия симметрии по всем аргументам. При этом нас будет интересовать конечный результат для функции истинности этой операции, который, естественно, является линейной комбинацией трёх симметрических многочленов:

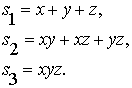(1)

Общая формула для совокупности рабочих компонент имеет вид:

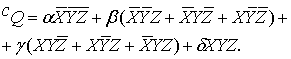(2)

Параметры могут принимать значения из множества {0;1}.

Сначала мы перечислим все возможные варианты, а затем найдём явные выражения для функций истинности этих операций (будем для сокращения обозначать их аббревиатурой СТО).

2. Прежде всего, заметим, что, при, будут получаться СТО, связанные с внешним отрицанием тех СТО, которые соответствуют значению . Поэтому здесь сначала рассмотрим все возможные случаи для нулевого значения первого параметра, а остальные СТО выразим, как внешние отрицания уже полученных СТО. Все получающиеся СТО мы будем нумеровать с помощью двоично-десятичной схемы, которая в данном случае становится удобной.

Для сокращения табличных записей введём дополнительные обозначения для совокупностей рабочих компонент:

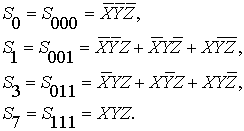(3)

Укажем строение полей Канта для совокупностей рабочих компонент во втором и третьем случаях, так как первый и последний случаи очень просты. Для второго случая () получаем:

Y X	0		1
0
		Z
1

Аналогично и для третьего случая, когда рассматривается , находим:

Y X	0		1
0
		Z
1

Отметим, что при объединении все четыре симметричных компоненты определяют точное полное покрытие универсума без наложений и пересечений, то есть, правильное покрытие. Подобные поля Канта могут быть построены и для самих симметричных тернарных операций, к определению которых мы теперь переходим.

Все возможные СТО при нулевом первом параметре определяются следующей таблицей:

№				Вид формулы
0	0	0	0
1	0	0	1
2	0	1	0
3	0	1	1
4	1	0	0
5	1	0	1
6	1	1	0
7	1	1	1

3. Значения искомых функций истинности для СТО, полученных в этой таблице, будем обозначать малыми латинскими буквами с соответствующими индексами:

(4)

При этом мы сразу будем записывать окончательные результаты для значений этих функций истинности через симметрические многочлены (1):

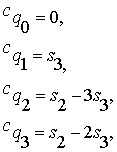(5)

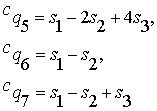
Другие восемь СТО получаются из построенных путём внешнего отрицания, что сразу приводит к результатам:

. (6)

4. В общем случае все полученные СТО могут быть выражены через симметрические многочлены (с добавлением единичного многочлена

). Коэффициенты этих линейных комбинаций мы будем называть спектром СТО и обозначать через где k – номер СТО.

В результате получаем спектральную таблицу всех СТО, в которой указываются коэффициенты их спектров.

,к	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
	0	0	0	0	1	1	1	1	0	0	0	0	-1	-1	-1	-1
	0	0	1	1	-2	-2	-1	-1	0	0	-1	-1	2	2	1	1
	0	1	-3	-2	3	4	0	1	0	-1	3	2	-3	-4	0	-1

Заметим в заключение, что все остальные тернарные операции являются композициями СТО и внутренних отрицаний различных видов (по одному, двум или трём переменным).

Рассмотрим некоторые конкретные примеры вычисления этих формул.

a) Для вычисления получаем:

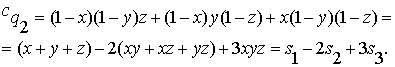
б) Для вычисления аналогично находим:

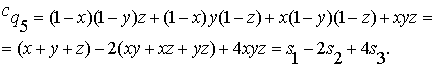
в) Для вычисления соответственно получаем:

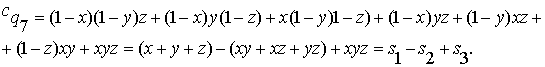
5.Аналогично можно рассмотреть и симметричные логические операции с четырьмя исходными высказываниями, то есть, квадра – операции, так как все рассуждения и вычисления в этом случае аналогичны выполненным. Поэтому кратко остановимся только на результатах этих исследований.

Симметричные многочлены от четырех переменных можно записать в виде:

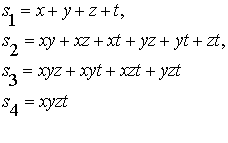(7)

Симметричная логическая квадратичная операция имеет следующий вид:

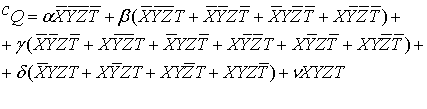(8)

Эту формулу также представим в упрощенном виде:

(9)

Учитывая реальный вид матрицы симметричной квадра-операции, получим ее схематическое представление через блоки, указанные в формуле (9).

МАТРИЦА СИММЕТРИЧНОЙ

КВАДРА-ОПЕРАЦИИ

T		0	0	1	1
Z	Y X	0	1	0	1
0	0
0	1
1	0
1	1

Основная таблица получается также при .

№					Вид формулы
0	0	0	0	0	= 0
1	0	0	0	1	=
2	0	0	1	0	=
3	0	0	1	1	= +
4	0	1	0	0	=
5	0	1	0	1	= +
6	0	1	1	0	= +
7	0	1	1	1	= + +
8	1	0	0	0	=
9	1	0	0	1	= +
10	1	0	1	0	= +
11	1	0	1	1	= + +
12	1	1	0	0	= +
13	1	1	0	1	= + +
14	1	1	1	0	= + +
15	1	1	1	1	= + + +

Теперь, учитывая, что , получаем значения функции истинности для всех построенных симметричных операций:

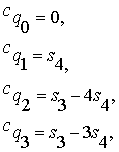
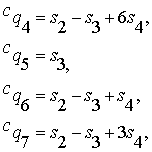
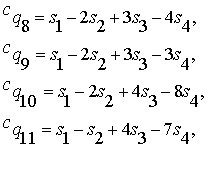
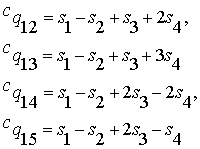
Позволим себе не составлять спектральную таблицу, так как все действия аналогичны уже выполнявшимся для тернарного случая. Отметим только, что большинство многослойных симметричных логических операций оказывается неразложимыми на композиции операций более низкого порядка.

ЛИТЕРАТУРА:

1. Ю.Л.Ершов, Е.А. Палютин. Математическая логика. СПб. 2005.

2. Дж.Шенфилд. Математическая логика. М.«Наука». 1975

3. Евсеев В.И. Логика. Монография. «ТАРИ». Казань. 2001.