Литвин О.М., Нікітіна О.В.

Бердянський державний педагогічний університет, Україна

ПОБУДОВА СПЛАЙНА 4-ГО СТЕПЕНЯ НА НЕРІВНОМІРНІЙ СІТЦІ ВУЗЛІВ МЕТОДОМ

ЛИТВИНА-ТКАЧЕНКА

Постійний технологічний розвиток апаратного забезпечення в сучасному світі вимагає створення та впровадження ефективних методів та моделей оброки даних. Одним з таких методів є застосування інтерполяційних сплайнів, значну увагу яким, у своїх роботах приділяють Литвин О.М., Литвин О.О., Ткаченко О.В. та ін..

Розглянемо алгоритм побудови В-сплайна четвертого степеня на нерівномірній сітці вузлів. Для цього запишемо формулу для третьої похідної В-сплайна четвертого степеня у вигляді сплайна першого степеня на інтервалі , враховуючи при цьому, що :

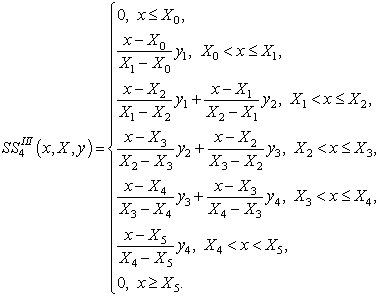
Графік для третьої похідної В-сплайна четвертого степеня зображено на рис. 1.

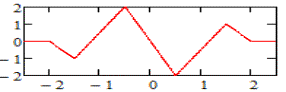
Рис. 1. Графік функції

Формулу для другої похідної В-сплайна четвертого степеня отримуємо за формулою:

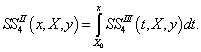
Графік для другої похідної В-сплайна четвертого степеня зображено на рис. 2.

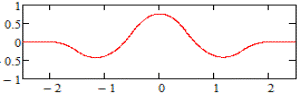
Рис. 2. Графік функції

Формулу для першої похідної В-сплайна четвертого степеня отримуємо за формулою:

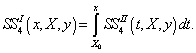
Графік для першої похідної В-сплайна четвертого степеня зображено на рис. 3.

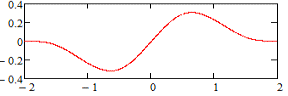
Рис. 3. Графік функції

Згідно алгоритму, ми побудовали сплайн четвертого степеня на інтервалі . Для знайшли значення сталих Поклали .

Побудований сплайн на інтервалі має вигляд:

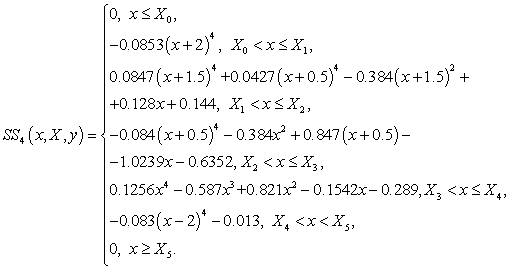
Графік сплайна четвертого степеня на інтервалі зображено на рис. 4.

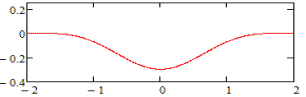
Рис. 4. Графік функції

Таким чином, ми побудували сплайн 4-го степеня на нерівномірній сітці вузлів методом Литвина-Ткаченка та графік для нього.

Література

1. Литвин О.М. Інтерлінація функцій та деякі її застосування / О.М. Литвин. – Х. : Основа, 2002. – 544.

2. Ткаченко О.В. Математичне моделювання поверхонь тіл складної геометричної форми з використанням інтерлінації та інтерфлетації функцій: дис. кандидата фіз.-мат. наук: 01.05.02 / Ткаченко Олександр Володимирович. – Х., 2011. – 128 с.