К.ф.-м.н. Постников Б.М.

Северный государственный медицинский университет, Россия

Некоторые интересные примеры, характеризующие глубину понятия параметрической линии

Понятие линии (или кривой) играет важнейшую роль в математике и в других науках. Многочисленные интересные примеры линий (ниже рассмотрены некоторые из них) показывают, что это понятие является сложным и многогранным.

К введению понятия линии существуют различные подходы. Например, плоская линия по Кантору определяется как континуум на плоскости, не имеющий внутренних точек (континуум - связное и компактное множество). Это определение оказалось пригодным только для плоских кривых. Наиболее общим является определение линии по Урысону. Согласно нему линия (на плоскости и в пространстве) определяется как континуум размерности единица. Очень удачное и важное понятие размерности множества было дано Урысоном. Для плоских линий определения Кантора и Урысона оказались эквивалентными.

Мы же подробно рассмотрим другой подход к определению линии – параметрический. Он является наиболее популярным и весьма удобным для практических целей, хотя и не лишён некоторых недостатков. В этой статье мы ограничимся рассмотрением только плоских параметрических линий. Сначала мы проанализируем взаимосвязи некоторых их свойств, характеризующие глубину понятия параметрической линии, а затем укажем интересные модификации некоторых известных линий.

Определение 1. Плоское множество , заданное в прямоугольной декартовой системе координат уравнениями

, ,

где функции и непрерывны на отрезке , назовём параметрической линией.

Параметрическую линию называют ещё линией по Жордану.

Определение 2. Если (в условиях определения 1) отображение , где , является биекцией (т.е. любым двум различным значениям параметра соответствуют различные точки линии), то параметрическую линию назовём параметрической дугой.

Если параметр истолковать как время, то параметрическую линию можно истолковать как траекторию движущейся по ней некоторой точки М. В общем случае, у параметрической линии могут иметься точки, через которые точка М проходит не менее двух раз. Такие точки называют кратными точками (или точками самопересечения) параметрической линии. Специфика параметрической дуги состоит в том, что она не имеет кратных точек (т.е. движущаяся по ней точка М проходит через все её точки в точности по одному разу).

Частным случаем параметрической дуги является график непрерывной числовой функции f на отрезке , т.к. он задаётся уравнениями

, .

Договоримся везде в дальнейшем плоскую меру по Лебегу (по Жордану) называть площадью по Лебегу (по Жордану).

Часто формирующееся интуитивное представление о параметрической линии как о линии, которую можно «нарисовать непрерывным движением пера», или как о «тонком штрихе, вьющемся на плоскости», или как об объекте, который «не имеет ширины» (т.е. имеет нулевую площадь), является весьма упрощённым, а иногда и обманчивым. Во-первых, известно, что параметрические линии могут иметь бесконечную длину (их называют неспрямляемыми). Поэтому «нарисовать» такие линии невозможно. Заметим, что бесконечную длину может иметь даже график непрерывной на отрезке функции – весьма частный случай параметрической линии. Во-вторых (и это ещё более впечатляет), параметрические линии могут иметь положительную площадь по Жордану. Например, ещё в 1890году Пеано построил параметрическую линию, целиком заполняющую квадрат. Это противоречит интуитивному представлению о линии как об «одномерном» объекте (т.е. «не имеющем ширины»). Появление в математике этой и аналогичной ей линий сыграло в своё время большую мировоззренческую роль. Такие примеры показывают, что понятие линии является очень сложным математическим понятием и требует глубокого изучения и осознания.

Далее мы рассмотрим ещё некоторые интересные примеры параметрических линий с весьма необычными свойствами. Сначала заметим, что заполняющая квадрат параметрическая линия Пеано, очевидно, имеет бесконечную длину (неспрямляема), поскольку спрямляемые линии имеют нулевую площадь по Жордану. К тому же из её построения можно увидеть, что она имеет кратные точки, т.е. не является параметрической дугой. И это по существу, т.к. вообще никакая параметрическая дуга не может заполнить квадрат, поскольку она не может иметь внутренних точек. Это следует из общих топологических соображений. Действительно, параметрическая дуга является гомеоморфным образом отрезка. А при гомеоморфизме (по теореме Брауэра об инвариантности области) внутренняя (граничная) точка множества переходит во внутреннюю (граничную) точку его образа (см., например, ). Кстати, из того факта, что параметрическая дуга не имеет внутренних точек, сразу же следует ещё более сильное утверждение: параметрическая дуга является нигде не плотным множеством. ( В противном случае, её замыкание, совпадающее в силу её замкнутости с ней самой, имело бы внутренние точки.)

Таким образом, параметрическая дуга (как не имеющая внутренних точек) не может иметь положительную площадь по Жордану. Поэтому может возникнуть естественное предположение: любая параметрическая дуга имеет нулевую площадь по Жордану. Такое предположение хорошо согласуется с нашим интуитивным представлением о линии.

Но по логике остаётся ещё одна возможность: существуют неквадрируемые по Жордану параметрические дуги. Такая дуга обязана быть неспрямляемой, т.к. спрямляемая параметрическая линия имеет нулевую площадь по Жордану. К тому же она не может быть графиком функции, т.к. график непрерывной на отрезке функции (даже неспрямляемый), как известно, тоже имеет нулевую площадь по Жордану. Поэтому это должна быть параметрическая (в собственном смысле этого слова) дуга. Примеры таких параметрических дуг были построены. Например, в книге построен пример параметрической дуги, проходящей в единичном квадрате и имеющей площадь по Лебегу не меньшую, чем , где - произвольное наперёд заданное положительное число. Таким образом, параметрическая дуга может «почти полностью» (в смысле площади по Лебегу) заполнить квадрат. Нетрудно понять, что эта параметрическая дуга не измерима по Жордану. Заметим, что рассмотренная линия имеет очень сложное построение. Более прозрачное для восприятия построение параметрической дуги с аналогичными свойствами можно получить исходя из другого интересного примера параметрической дуги L , рассмотренной в . Дуга L возникает при конструировании авторами неквадрируемой жордановой области. Сначала мы обсудим важные для нас свойства этой дуги L , а затем покажем, как можно построить некоторые интересные её модификации.

Дуга L строится следующим образом. ( Приводимое ниже описание построения дуги L незначительно отличается от описания, приведённого в .) Рассмотрим на координатной плоскости треугольник с вершинами O(0, 0) , A(1, 1) , B(2, 0). Он имеет площадь, равную единице. На первом шаге построения мы удалим из треугольника полуоткрытый треугольник (без боковых сторон и ), вершины C и D которого лежат на отрезке , причём , . Площадь удаляемого полуоткрытого треугольника равна . Полученная в результате фигура изображена на рис. 1 (она заштрихована).

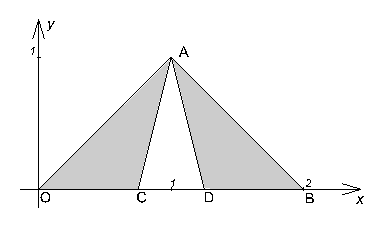
Рис. 1

Она состоит из двух треугольников первого ранга: и . На втором шаге мы из каждого из этих двух треугольников аналогичным образом удалим по одному полуоткрытому треугольнику: и , сумма площадей которых равна . Полученная в результате фигура изображена на рис. 2 .

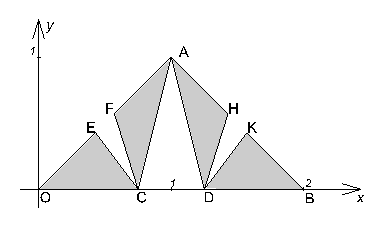
Рис. 2

Она состоит из четырёх треугольников второго ранга: , , , ( , ). По индукции на n-ом шаге нашего построения из фигуры мы удалим полуоткрытых треугольников, сумма площадей которых равна . Полученная в результате фигура состоит из треугольников n - го ранга. На рис. 3 изображена фигура при n=3.

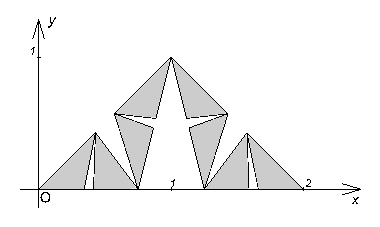
Рис. 3

Эту процедуру можно продолжать неограниченно. Рассмотрим фигуру , которая после её параметризации и будет интересующей нас параметрической дугой L . Другими словами, дуга L получается в результате удаления из треугольника объединения счётной совокупности полуоткрытых треугольников, удаляемых на всех возможных шагах (т.е. при всех ) описанного выше построения. Очевидно, что L можно представить также и как множество всевозможных точек, каждая из которых является единственной общей точкой для всех треугольников некоторой последовательности . Здесь - один из составляющих фигуру треугольников n - го ранга, причём содержится в при всех . При этом следует учесть, что по построению при +, где - диаметр треугольника (т.е. наибольшая из длин его сторон). Таким образом, последовательность - «стягивающаяся» последовательность «вложенных» треугольников. Указанное представление для L лежит в основе её параметризации. Процедура параметризации фигуры L подробно описана в [3]. (Это достаточно длинное описание не лишено некоторых «шероховатостей», но они без особого труда преодолеваются.) Мы здесь не будем повторять эту рутинную и утомительную процедуру. Заметим только, что она аналогична процедуре параметризации квадрата в виде линии Пеано. Но, в отличие от последней, параметризация дуги L получается простой, т.е. не имеющей кратных точек, и в результате L становится параметрической дугой.

Через будем обозначать площадь по Лебегу множества A , а через площадь по Жордану множества A. Найдём площадь по Лебегу параметрической дуги L. Пусть CL - дополнение L до треугольника , т.е. объединение совокупности всех «удаляемых» полуоткрытых треугольников. В силу счётной аддитивности меры Лебега множество CL измеримо по Лебегу и Поэтому дуга L , как дополнение множества CL до треугольника , тоже измерима по Лебегу и . Итак, дуга L имеет площадь по Лебегу, равную .

Выясним теперь вопрос о её площади по Жордану. Для любой многоугольной фигуры M , содержащей L, в силу монотонности меры Лебега имеем: . С другой стороны, для многоугольных фигур , которые содержат L , получаем: , т.е. при + . Поэтому для внешней площади по Жордану дуги L имеем:

.

Как мы отмечали ранее, любая параметрическая дуга не имеет внутренних точек. ( Впрочем, для дуги L это непосредственно видно и из её построения.) Поэтому внутренняя площадь по Жордану дуги L . Итак, , т.е. L не измерима по Жордану. Очевидно, что этот факт (с помощью аналогичных рассуждений) получает следующее обобщение: любая параметрическая дуга l , имеющая положительную площадь по Лебегу, не измерима по Жордану (для неё , а ). Попутно заметим, что не существует параметрических линий (в том числе и параметрических дуг), имеющих нулевую площадь по Лебегу, но неизмеримых по Жордану. Действительно, параметрическая линия является компактом, а из критерия компактности Бореля – Лебега легко следует, что компактное множество имеет нулевую площадь по Лебегу тогда и только тогда, когда оно имеет нулевую площадь по Жордану.

Используя идею построения параметрической дуги L, уже нетрудно построить параметрические дуги «почти полностью» (в смысле площади по Лебегу) заполняющие треугольник, квадрат, круг и некоторые другие фигуры.

В случае треугольника изменения описанного выше построения дуги L будут минимальны. Зададим произвольное число . На n-ом шаге построения из фигуры будем удалять полуоткрытых треугольников, сумма площадей которых равна . Тогда и .

В случаях квадрата, круга и некоторых других фигур построения аналогичны.

В заключение отметим, что дуга L , являясь гомеоморфным образом отрезка, т.е. множества нулевой площади по Лебегу, сама имеет положительную площадь по Лебегу. Это означает, что свойство множества иметь нулевую площадь по Лебегу, а также свойство множества иметь положительную площадь по Лебегу, вообще говоря, не сохраняются при гомеоморфизмах, т.е. не являются топологическими инвариантами. Поскольку дуга L не измерима по Жордану, то аналогично получаем, что свойство множества быть измеримым по Жордану, а также свойство множества иметь нулевую площадь по Жордану тоже не являются топологическими инвариантами.

Литература:

1. Александров П.С. Введение в теорию множеств и общую топологию. - М.: Наука, 1977. - 368 с.

2. Гелбаум Б., Олмстед Дж. Контрпримеры в анализе. - М.: Мир, 1967.-251 с.

3. Ильин В.А., Позняк Э.Г. Основы математического анализа, ч.1. - М.: Наука, 1982. - 616 с.