ОБ УРАВНЕНИЯХ ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ СИСТЕМ С СЕРВОСВЯЗЯМИ

Тешаев М.Х., Ахмедов М.Ш.,Сайфуллаев С.С.

Бухарский инженерно-технологический институт

Аннотация. Рассматривается механическая система, состоящая из переносящего твёрдого тела и N материальных точек (носимые тела). Система стеснена обычными идеальными связями и сервосвязями. С учетом параметрического освобождения системы от сервосвязей получены уравнения движения.

Ключевые слова. Переносящее тело, носимые тела, сервосвязь, реакция сервосвязи.

Рассмотрим механическую систему, состоящую из переносящего твёрдого тела и N материальных точек (носимые тела), положение которых относительно системы координат Oxyz, связанной с переносящим телом, определяется обобщёнными координатами q₁, q₂ , … , q_n .

Положение переносящего тела в инерцианальной системе координат будем определять шестью обобщёнными координатами : координатами полюса и углами Эйлера , задающими ориентацию подвижной системы координат Оxyz в системе .

Пусть на движении переносящего тела наложены обычные линейные неголономные идеальные связи

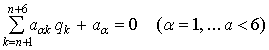(1)

где - функции от обобщённых координат переносящего тела и t.

На относительное движение носимой системы наложены обычные линейные неголономные идеальные связи

(2)

где зависят от обобщённых координат и t.

Допустим, что система ещё стеснена сервосвязями /1/ вида

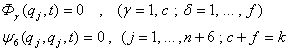(3)

Предполагается, что среди возможных перемещений имеются такие, определяемые уравнениями

(6)

на которых реакции сервосвязей работы не производят /2/. Здесь .

Известно, что сервосвязи не выполняются точно /2/, т.е. наряду с соотношениями (3) имеют место и соотношения, соответствующие преобразованию системы с сервосвязями (3) к виду /2/ :

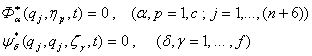(7)

где - параметры, характеризующие освобождение системы от сервосвязей (3). Нулевые значения параметров соответствуют связям (3) и их продифференцированным формам. За эти величины могут быть взяты, например, левые части уравнений (3), вычисляемые на действительном движении системы /3/.

Обозначив через N_p и P реакции, отнесённые к параметрам , будем предполагать, что последние вынужденно изменяются согласно дифференциальным уравнениям /2/

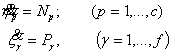(8)

Определяя работу принуждений на перемещениях выражением

для параметрически освобождённой системы будем иметь

(9)

где - реакции связей второго рода.

Пусть из способа действия реакций связей второго рода следует, что на (А) – перемещениях (6) работа реакций связей второго рода равна нулю как для неосвобождённой, так и параметрически освобождённой системы. Тогда при произвольных принуждённых реакций работа (9) обратиться в нуль при /1/

.

С учётом первой группы уравнений (7) вместо обобщённых координат q₁, … , q_a введём параметры .Тогда из общего уравнения динамики

,

где Т- кинетическая энергия; - обобщенная сила, отнесенная к координате ,

при условиях (4) – (6) будем иметь:

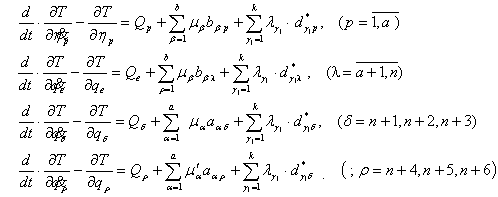(10)

где- множители связей, .

Уравнения (10) представляют собой дифференциальные уравнения относительного движения с множителями связей. А слагаемые

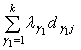
представляют собой обобщённых реакций связей второго рода (сервосвязей).

Литература

1. Беген, А. Теория гироскопических компасов М.: Наука, 1967.-192 с.

2. Тешаев М.Х. К задаче стабилизации движений механических систем, стесненных геометрическими и кинематическими сервосвязями. Известия вузов. Поволжский регион. 2009 .№ 4 (12).- С. 27-38

3. Галиулин А.С. Мухарлямов Р.Г., Мухаметзянов И.А. Фурасов В.Д. Построение систем программного движения. М.: Наука, 1971-352 с.