P. Begun, D. Rubashova

Saint Petersburg Electrotechnical University "LETI"

METHODS AND ASSESSMENT OF SYSTEM INTRAOCULAR PRESSURE IN KERATOCONUS

There are several methods for measuring intraocular pressure. The Maklakov’s method is the most common in Russia. The method of determining intraocular pressure by Maklakov’s tonometer is based on installing a particular weight with a flat surface on the eye. Under load, the surface of the eyeball flattened by tonometer’s contact surface to a certain flattening circle. The value of the tonometric intraocular pressure is determined according to the diameter of the flattening circle of corneal by the contact part of the tonometer. To converse the tonometer readings to pressure in the unit mm Hg. Art. special calibration tables or straightedges are required. Internals of the eyeball’s structures are not taken into account while measuring of intraocular pressure.

Numerous studies in the field of ophthalmology has shown that the variability of the thickness and curvature of the cornea significantly affect the results of tonometry. But, the influence of keratoconus on the measurement’s results has not been considered yet.

The corneal curvature radius and the thickness of the central zone changes with keratoconus. Ultimately it becomes thinner and takes a conical shape (Fig. 1). There are three stages of keratoconus:

At the first stage of keratoconus there are reduction of visual acuity, decrease in the radius of curvature of the cornea to 7.5-7.2 mm, decrease of the thickness of the central corneal zone to 0.48 mm;

At the second stage of the disease the deformation of the cornea progresses, the radius of curvature decreases to 7,1-6,75 mm, the thickness of the central zone of the corneal - to 0.44 mm;

At the third stage the cornea becomes thinner, and its radius decreases to 6,7-6,0 mm, the thickness of the central corneal zone - to 0.40 mm.

To investigate tonometric IOP in normal and keratoconus development model was built based on the eye orbit connective tissue formations (Fig. 1). Tonometric IOP was calculated sequence of iterations as a result of which the volume is not the flattened area of the deformed eye includes an additional amount of fluid displaced from corneal tonometer:

1. Defined volumes: a) deformed eyes, b) aqueous humor displaced tonometer flattened part of the eyeball, in) is not the flattened area of the deformed eyeball;

Fig. 1 The scheme of the model of the eye with the connective tissue formations orbit

2. Conditions of zero displacement in the cornea, in the contact zone with the tonometer, calculated displacement and deformation is not flattened cornea and sclera;

3. Assuming a linear relationship between load and displacement, as defined in claim 2 nonoblate character deformation of the eye , increased its volume by 0.9 volume of fluid displaced by the tonometer;

4. Similarly, paragraph 2 provides the equilibrium condition in the contact zone of the deformed cornea and the tonometer;

5. Defines the scope of the non-flatness of the eyeball;

6. If the volume is not different from the flattened part of the original volume of the eyeball, amended in accordance with paragraph 3 (increases or decreases the volume of the eye is not flattened;

7. If necessary, consistently repeated the calculations in accordance with § 4-6.in accordance with р. 4-6.

Research of keratoconus’s influence on the parameters of intraocular pressure is held with applanation load of 10 g and with the diameter of the flattening circles are 3, 4, 5, 6 and 7 mm. Compliance of the diameter of the flattening circle and the tonometric pressure P_М is established according to B.L. Polyak’s rule.The geometric constructions of the models were developed by the Solid Works computer program. Stress-strain condition was calculated by Cosmos Works finite-element software.

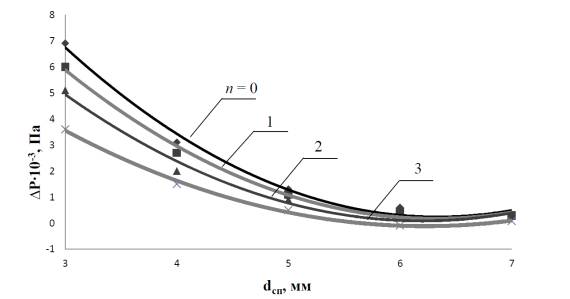
Fig. 2 shows the difference between the value of the tonometric intraocular pressure detected by the Maklakov’s method in accordance with the rule of B.L. Polyak and tonometric intraocular pressure, calculated according to the first model, from the diameter of the flattening circle of the cornea in a normal state (n = 0) and at the next three stages of keratoconus (n = 1, 2, 3).

In the study of the influence of keratoconus on tonometry results introduced the following sumptions: 1) the material of the cornea, sclera, dura mater, tennonov’s capsules, fasciae musculares materials, episcleral space and orbital bones is uniform, solid and isotropic with reduced modulus of resilience; 2) the model is rigidly fixed on the outer side of the eye socket bone; 3) modulus of resilience of the cornea E_P = 0.362 MPa, modulus of resilience the contact part of the tonometer E_T = 210 GPa; reduced modulus of sclera, dura mater, tennonov’s capsules, resilience fasciae musculares, episcleral space and orbital bones are equal respectively E_C = 6 MPa; E_TMO = 150 MPa; E_ТК = 200 MPa; E_CT = 20 MPa, E_Э= 30 kPa, E_К = 2.5 GPa. 4) the radius of curvature of the cornea in a normal state (n = 0) R_КР = 7.8 mm, the central zone thickness h_РЦ = 0,52 mm, thickness at the periphery of the cornea assumed to be constant at all stages of keratoconus h_РП = 0.6 mm. At the next three stages (n = 1, 2, 3) cornea changes its curvature R_КР = 7.2 mm (n = 1), 6.8 mm (n = 2) and 6.2 mm (n = 3) and central zone thickness, respectively h_РЦ = 0.48 mm, 0.44 mm and 0.4 mm; thickness and radius of curvature of the sclera H_C = 0.7 mm R_KC = 12 mm, diameter dura mater D_H = 2.1 mm; the thickness and radius of curvature tennonov’s capsule H_TK = 0.74 mm, R_TK = 13 mm; dimensions fasciae musculares T_СТ = 5 mm, t_СT1 = 11.25 mm, t_СT2 = 16 mm, h_СT1 = 0.7 mm, h_СT2 = 1.76 mm, outer diameter fasciae musculares d_СT = 36.7 mm, height of the orbit Н_Г = 52.5 mm outer diameter orbit D_Г = 49 mm, inner diameter of the orbit d_Г = 33 mm.

Fig. 2. The dependence of the difference between the value of the tonometric intraocular pressure detected by the Maklakov’s method in accordance with the rule of B.L. Polyak and tonometric intraocular pressure, calculated according to the fourth model, from the diameter of the flattening circle.

The model is divided into 70000 tetrahedral finite elements. With the increasing of the stage of keratoconus development Corneal of the eye becomes more pliable. When flattening circles are from 7 mm to 3 mm, intraocular tonometric pressure increases relative to the norm from 10, 8% to 37.3%. With the increasing of the stage of keratoconus's development the discrepancy of calculated tonometric intraocular pressure and tonometric intraocular pressure detected by the Maklakov’s method decreases.