Лысенко М. Г., Матвийчук А. В.

Национальный технический университет Украины "КПИ"

ИСТОРИЯ РАЗВИТИЯ УЧЕНИЯ О КОРПУСКУЛЯРНЫХ

СВОЙСТВАХ ЭЛЕКТРОМАГНИТНОГО ИЗЛУЧЕНИЯ

1. По отношению к истории развития квантовой теории теплового излучения Планка история теории корпускулярных свойств электромагнитного поля (фотона) имеет свои особенности. И начало, и окончательное формулирование квантововой гипотезы теплового излучения принадлежит М. Планку. Что касается теории фотона, то эта теория была начата А. Эйнштейном, но дальнейшее ее развитие принадлежит другим авторам, в частности, П. Дираку. На наш взгляд, это привело к разнобою преподавания темы „фотон” в учебниках. Целью нашей работы является анализ развития указанной темы в учебниках общей физики.

В данной работе проанализировано свыше 30 учебников общей физики на предмет освещения темы. Парадоксальным есть тот факт, что изложение темы в учебниках остановилось на уровне развития науки двадцатых годов прошлого столетия. Дальнейшее, после двадцатых лет развитие физической науки, во-первых, подтвердило новыми опытами корпускулярные свойства электромагнитного излучения, во-вторых, значительно развило теорию фотона. Это широко представлено в учебниках квантовой механики и квантовой электродинамики. Как итог, имеет место расхождение в преподавании. На старших курсах высших учебных учреждений при изучении квантовой механики трактовка понятия “фотон” принципиально отличается от понятия, полученного в школе и на младших курсах при изучении общей физики.

2. Рассмотрим основные выводы учения о фотоне в историческом развитии; подчеркнем, что расхождение в преподавании связанны именно с историей развития учения о фотоне.

Год 1905 – А. Эйнштейн успешно объясняет основные свойства фотоэффекта на основе понятия “квант света” (корпускула света). Предложенная модель успешно объясняет основные свойства фотоэффекта, но противоречит волновой теорией. Большинство известных физиков того времени, в том числе, Нобелевские лауреаты М. Планк и В. Вин, отрицали существование корпускулярных свойств света. Аргументом для возражения выдвигалось совершенство теории электромагнитных волн Максвелла. Дале мы увидим, что в этом оппоненты А. Эйнштейна были правы. Как доказательство несправедливости теории квантования света, например, в Википедии [6] приведенные ссылки на эксперимент по дифракции света с энергией одного фотона (1907 г.). Одновременно при этом справедливо считать, что гипотеза А. Эйнштейна опередила свое время. Прибавим также, что позднее квантовая теория подтвердила теорию Эйнштейна для фотоэффекта без использования корпускулярных свойств света (напр., [9]), а потом теоретически обосновала его гипотезу, исходя из новых позиций.

Год 1923 – А. Комптон публикует результаты своих известных экспериментов по рассеянию рентгеновского излучения на веществе. Волновая теория не может объяснить изменение длины рассеянной волны. Корпускулярная теория электромагнитного излучения это объясняет блестяще.

Год 1924 – Л. де Бройль предлагает гипотезу о волновых свойствах корпускул, которая полностью подтверждается опытами. Очевидно, что гипотеза де Бройля есть творческим продолжением гипотезы Эйнштейна.

Год 1926 – возникновение названия “фотон” (Г. Льюис). Бурно развивается квантовая механика. На ее основе делается попытка согласовать корпускулярные свойства света с волновыми. Как следствие, формулируется концепция корпускулярно-волнового дуализма: полная тождественность волновых и корпускулярных свойств корпускул и электромагнитного поля. В соответствии с положениями корпускулярно-волнового дуализма, фотон считается образованием, энергия которого сконцентрирована в маленьком объеме пространства: “дробинкой”, по высказыванию Борна. По этой теории положение фотона в просторные описывается вероятностными законами: плотность энергии электромагнитного поля в заданной точке считается пропорциональной концентрации фотонов в этой точке. Именно эта модель фотона наиболее представлена в учебниках общей физики.

Год 1927 – преодолеть противоречие между квантовыми и волновыми свойствами света удалось английскому физику П. Дираку. К электромагнитному полю Дирак применил математический аппарат квантовой механики. Дирак рассматривает поле в виде бесконечного количества стоячих электромагнитных волн в определенном объеме (резонаторе) [19]. Совокупность осцилляторов представляет собой бесконечное количество степеней свободы, энергия поля распределяется по степеням свободы (осцилляторах). Использовав расчетный аппарат квантовой механики, Дирак заменил обобщенные координаты классической механики соответствующими квантово-механическими операторами (принцип соответствия), получил и решил уравнение Шредингера для электромагнитных колебаний. На основе решения были найдены волновые функции и энергия осцилляторов. Приведем полученную формулу для полной энергии Е электромагнитного поля:

(1)

где – постоянная Планка, – собственная частота колебаний k-того осциллятора, – квант энергии, – целое положительное число, равняется количеству квантов энергии осциллятора.

Теорию Дирака называют также квантовой теорией электромагнитного поля (фотона).

3.1. Рассмотрим первую сумму уравнения (1). Эта сумма обосновывает идею Эйнштейна о корпускулярных свойствах электромагнитных колебаний. Осциллятор принимает только дискретные значения энергии – кванты энергии, пропорциональные частоте. Количество квантов зависит от степени возбуждения осциллятора. Сам факт дискретизации энергии стоячих волн целиком заслуженно называют гипотезой Эйнштейна [35]. Остановимся на особенностях теории Дирака. В соответствии с теорией энергия фотона не концентрирована в определенной точке пространства (не материальная точка), Фотон распределен по всему объему, в котором существует электромагнитное поле; фотоны “размешаны” в пространстве – в каждой точке поля существуют колебания всех без исключения стоячих волн. Наблюдать существование фотона возможно при взаимодействии фотона с корпускулой лишь там где находится корпускула.

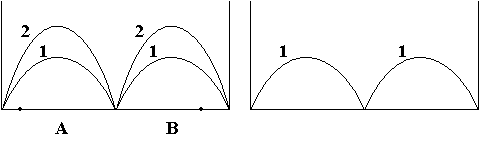
Проиллюстрируем это рисунком. На левом рисунке схематично изображено распределение квадрата напряженности электрического поля вдоль одного из направлений, пусть в этом направлении укладывается одна длина волны и энергия этой стоячей волны равняется двум фотонам; линия 2 соответствует двум фотонам, линия 1 – одному. Пусть в точке А находится объект, поглощающий один фотон. В соответствии с теорией Дирака поглощение происходит со всего объема, в котором находится электромагнитное поле, в том числе, из точки В. В результате после поглощения остается один фотон, которому соответствует линия 1 (правый рисунок). Вероятность взаимодействия в заданной точке пространства пропорциональная плотности энергии электромагнитного поля в этой точке, но поглощение происходит со всего объема. Обращаем также внимание на то, что узел стоячей волны делит фотон на части (две в нашем случае), а поглощается, или возбуждается фотон, как единое целое.

При объяснении интерференции и дифракции света, например, в опыте Юнга, в соответствии с квантовой теорией фотон может проходить одновременно через обе щели. Это можно представить таким образом. Источник света, например, выходное зеркало лазера, экран с двумя щелями и экран для наблюдения образуют резонатор, в котором создаются стоячие волны. Каждая стоячая волна и, соответственно, каждый фотон находятся во всех точках резонатора, в том числе, в обеих щелях. В особенности проявляется различие между фотоном и корпускулой при переходе к макроскопической теории. Квантовой корпускуле в макроскопической теории соотносится микрочастица, движущаяся по классической траектории; фотону в классической физике соответствует неограниченная в пространстве и времени плоская монохроматическая волна.

Расчеты теории Дирака подтверждают теорию Эйнштейна для фотоэффекта и теорию Комптона, но из позиций квантовой механики; расчеты объясняют также другие опыты по взаимодействию света с веществом и не противоречат волновой теорией.

3.2. Параллельно с теорией Дирака к аналогичным выводам приводит и соотношение неопределенностей для фотона [35]. Как известно, соотношение неопределенностей – соотношение Гейзенберга – в квантовой механике введено для квантовых частиц и является следствием волновых свойств корпускул; неопределенность присущая прежде всего колеблющемуся (волновому) движению. Действительно, для колебаний невозможно точно определить частоту за бесконечно малый промежуток времени. При переходе к координате x и длине волны для электромагнитных волн соотношения определяет взаимосвязь расстояния на которой измеряется длина волны с точностью ее измерения. Математически соотношение имеет вид:

, , (2)

где , – неопределенность координаты, длины волны и частоты;
– скорость светлая.

Сравним соотношение для фотона с соотношением для корпускул. Для квантовых частичек соотношения связано с точностью одновременного определения координаты и импульса частицы. Многочисленные опыты подтверждают ограниченность корпускулы в пространстве и простейшей ее моделью является материальная точка.

Что касается фотона, то такое понимание есть ошибочным. Для электромагнитной волны соотношение представляет собою свойство волнового движения. Автоматически, соотношение переносится на квант энергии (на фотон). При распространении плоской волны в направления x, энергия фотона и, соответственно, длина волны, или частота определены точно – фотон может быть распределен по бесконечному объему. Каждая стоячая волна заданной длины (каждый осциллятор) может включать в себя бесконечное количество фотонов в зависимости от энергии. И главное, не существует экспериментального подтверждения сходства фотона с материальной точкой и наблюдается фотон лишь тогда, когда поглощается корпускулой.

3.3. Возвратимся к формуле (1) и рассмотрим вторую сумму. Это сумма дискретных энергий, так называемых, “нулевых колебаний”. Энергия “вечного колебания” одного осциллятора равняется половине энергии фотона. Число осцилляторов бесконечное, в результате, бесконечна и суммарная энергия нулевых колебаний. В теории энергия нулевых колебаний взята за начало отсчета и не учитывалась. Но появились опыты, для объяснения которых используются нулевые колебания. Прежде всего, это сдвиг между уровнями 2S и 2P в атоме водорода(лэмбовский сдвиг). Полная достоверность получена в 1947 г. в опытах В. Лэмба и Р. Ризерфорда. Радиофизическими методами стимулирован прямой переход между уровнями энергии 2S и 2P атома водорода и вымеренное энергетическое расстояние между ними. Измеренное различие энергий соответствует частоте 1057 МГц. Исчерпывающее теоретическое объяснение сдвига дал Г. Бете [19]. В соответствии с его теорией, на движение электрона по орбите дополнительно накладывается хаотичное движение электрона под действием флюктуаций электромагнитного поля нулевых колебаний. Таким образом, опыты и теория подтверждают существование нулевых колебаний, которое одновременно является подтверждением правильности теории фотона Дирака.

4.1. Перейдем к анализу учебников. Мы условно разделили учебники и пособия по физике на две группы по годам издания. Первая группа – изданы до 1990 г. [5, 14, 20, 22-24, 27, 28, 32-35]; вторая – изданы после 1990 г. [1-4, 6-8, 10-13, 15-18, 21, 25, 26, 29-31]. Основой для деления взято время публикаций теории Дирака для фотона в научном журнале в 1927 г. и в научных изданиях в 1956 и 1959 гг. [19]. В учебники из квантовой механики теория включена в начале шестидесятых лет [9, 19].

4.2. Рассмотрение начнем с учебников по атомной физики Макса Борна [34] и Э. Шпольського [32], которые более всего повлияли на состояние освещения темы в общей физике. Эти издания впервые появились в 1933 и 1944 гг. и неоднократно переиздавались. В них фотон полностью отождествляется с квантовой корпускулой (материальной точкой). Прибавим к изложенному ссылку [34] на опыты Мейєра-Герлаха по фотоэффекту на мелких металлических крупинках. Непонятным для волновой теории был тот факт, что фотоэлектроны появлялись непосредственно после включения света. Соответственно волновой теории распределение энергии падающей волны может быть равномерным по объему металлической крупинки и накопление энергии для выполнения электроном работы выхода должно длиться несколько секунд. Поэтому при объяснении фотоэффекта волновая теория отклонена, а световой поток рассматривается, как движение дробинок со сконцентрированной в них энергией. Такая несовершенная трактовка сформулирована в начале развития современной квантовой теории. В дальнейшем, квантовая механика смогла объяснить фотоэффект, используя только волновые свойства света. В квантовой механике вычисляется вероятность переходов электрона между уровнями энергии атома. Формула Эйнштейна при этом является следствием волновых свойств корпускул, а не корпускулярных свойств света. Параллельно существует строгое объяснение фотоэффекта с точки зрения корпускулярной теории света на основе теории Дирака. Укажем, что при переходе к классическому приближению фотоэффект эквивалентен резонансному поглощению света высокодобротной колеблющейся системой, способной накопить достаточную энергию за короткое время.

В учебнике Борна [34] упоминается одним предложениям теория Дирака и трехмерность фотона (не материальная точка), как “...чисто абстрактную концепцию”. Такое отношение объясняется непривычностью теории Дирака для современников и отсутствием подтверждающих ее опытов.

В [32] дополнительно к изложенному изучаются флуктуации фотонов, которые полностью отождествляются с флуктуациями молекул идеального газа. Отметим также, что флуктуации электромагнитного поля легко описываются в рамках волновой теории.

Изложенная точка зрения в большем, или меньшем объеме повторяется в [3, 5, 10, 13, 14, 20-24, 29, 33] и переносится в [1, 2, 4, 7, 8, 11, 12, 15-18, 25, 26, 30, 31]. Остановимся на отклонениях от обобщенной точки зрения некоторых из них. Так, в [14] подчеркивается трудность объединения корпускулярных и волновых свойств фотона-дробинки. В учебниках для высшей [22, 23] и средней [21] школы справедливо утверждается тот факт, что корпускулярные свойства фотона проявляются при взаимодействии с веществом, а волновые – в явлениях интерференции и дифракции. Но при этом авторы не отходят от модели фотона – дробинки.

В [20] дано определение фотона, как физический объект, связанный с электромагнитным излучением, с энергией E=hv, Это правильно, но определение носит не конкретный характер. Далее утверждается неприемлемым представление фотона в виде некоторого, распределенного в пространстве, объекта и невозможность рассматривать фотон в виде “...пространственной области, заполненной электромагнитным полем...”. Утверждается также невозможность сопоставления фотону напряженности электрического поля, которым характеризуется световая волна. Такое утверждение диаметрально противоположное теории Дирака, в соответствии с которой фотон существует в пространстве, где находится поле. В противоположность [20], в физической теории есть много примеров вычисления напряженности электрического поля, исходя из энергии фотона [19].

В учебнике [24] представлен фотон, как “цуг” волн. Это неправильно по нескольким причинам. Назовем лишь то, что “цуг” характеризуется спектром частот, в то время, как частота фотона имеет только одно фиксированное значение. Большой интерес представляет точка зрения Р. Фейнмана, в его учебнике [27, 28] рассмотрено коротко, но из текста вытекает очевидная склонность к концепции фотона Дирака. Поток электромагнитной энергии представляется, как поток фотонов, который не вступает в противоречие с теорией Дирака; кроме того, для нахождения интенсивности светы рассматривается “...отдельный фотон, который падает, характеризуется определенной амплитудой попадания...”, а не вероятностью, как это должно выходить из корпускулярно-волнового дуализма. Модель фотона в виде дробинки не упоминается.

4.3. Рассмотрим состояние освещения темы в современных изданиях [1-4, 6-8, 10-13, 15-18, 21, 25, 26, 29-31]. Процитируем определение фотона из учебника [8]: фотон – квант энергии электромагнитного поля. Такое определение правильное, но для понимания нужны более детальные объяснения. В изданиях [1, 2, 4, 7, 8, 11, 15-18, 26, 30] фотон рассматривается сжато; во всех без исключения изданиях явным образом, или неявно фотон представлен локализованной частицей (дробинкой).

В [4, 7, 11] изложение отражает общее состояние и вторит рассмотренным изданиям прошлых лет, но тема изложена шире. Остановимся на этом. При рассмотрении соотношения для фотона использована формула Гейзенберга и ее трактовка для корпускул: невозможность одновременного определения координат и импульса. При этом, также как и для корпускул, фотон представлен в виде волнового пакета, то есть повторяется ошибка с [24]. Объясним это. Пакет волн аналогично с “цугом” имеет спектр частот и, соответственно, спектр энергий, а фотон по определению имеет фиксированную частоту и энергию. Дале при переходе к интерференции и дифракции фотон отождествляется с квантовой частицей. Продемонстрируем это цитатой с [4, 7]: “...квадрат амплитуды световой волны определяет вероятность попадания фотона в данную точку простанства, точнее – вероятность нахождения фотона в объеме dV пространства, что включает точку, которую рассматривают...”. Это утверждение противоречит современной теории [19]. В теории специально для такого случая доказано, что фотон не может концентрироваться в бесконечно малом объеме. Такое распределение ведет к нарушению закона сохранение энергии. Если для квантовой частички возможное вычисление среднего значения координаты, то для фотона такое вычисление некорректно и, соответственно, понятие о вероятности нахождения фотона в той, или другой точке пространства тоже некорректно.

Для сравнения рассмотрим изложение темы в учебнике американских авторов [25]. В нем просматривается такая же склонность рассматривать фотон в виде материальной точки. Например, в задаче по определению количества фотонов, которые падают на единицу площади поверхности. Исходя из того, что каждый фотон распределен по всей поверхности, в такой постановке задача неверная. Постановка станет правильной, если речь пойдет о взаимодействии электромагнитной волны с веществом.

5. Подведем итоги.

5.1. В рассмотренных учебниках общей физики приведенные правильные объяснения основных свойств фотоэффекта и других опытов по взаимодействию света с веществом, исходя из корпускулярных свойств света. Но корпускулярные свойства трактуются неверно. Корпускула света (фотон) при обобщениях полностью отождествляется с квантовой частицей, локализованной в пространстве: корпускулярно-волновой дуализм. Ни один из учебников не рассматривает квантовую теорию электромагнитного поля Дирака, или ее выводы.

5.2. В противоположность к изложенного, теория Дирака рассматривает электромагнитное поле, как непрерывное в пространстве – естественное свойство волнового движения. Квантуется лишь энергия: фотон – квант энергии электромагнитного поля. Таким образом, согласовываются корпускулярные свойства света с волновыми. Квантово-механический и волновой подходы подтверждают формулу Эйнштейна для фотоэффекта.

Литература:

1. Андріяшик М. В., Вербицький Б. І., Король А. М. Курс фізики: модульно-рейтингова система навчання: підручник для студ. техн. навч. закл. – К.: Фламенко, 2008. – 530с.

2. Барановський В. М., Черенков О. В. Загальна фізика: Курс лекцій:Навч. посіб. для студ. інж.-техн. спец. вищ. навч. закл. / Європейський ун-т / Валерій Михайлович Барановський (заг.ред.). – Ч. 3. – К.: Видавництво Європейського університету, 2004. – 204с.

3. Бутиков Е. И., Кондратьев А. С. Физика: Учеб. пособие:В 3 кн.. – М.: Физматлит, 2001. – (Для углубленного изучения). Кн. 2 : Электродинамика. Оптика. — 336с.

4. Бушок Г. Ф., Венгер Є. Ф. Курс фізики: Навч. посібник для студ. фіз.-мат. спец. вищ. пед. навч. закладів:У 2 кн. – К.: Либідь, 1997. – Кн. 2: Оптика; Фізика атома і атомного ядра; Молекулярна фізика і термодинаміка. – 421с.

5. Вихман Э. Квантовая физика: Учеб. руководство; Пер. с англ./ Под ред. А.И. Шальникова и А.О. Вайсенберга. – 3-е изд., испр. – М.: Наука. Гл. ред. физ.-мат. лит., 1986. – (Берклеевский курс физики)– 392 с.

6. Вікіпедія, тема “Фотон” http://ru.wikipedia.org/wiki/Фотон

7. Воловик П. М. Фізика для університетів: повний курс в одному томі. — К.; Ірпінь : Перун, 2005. — 864с.

8. Гончаренко С.У. Фізика: проб. навч. пос. для 11 кл. шк. ІІІ ступ., гімназій і ліцеїв гуманіт. проф. – 2-ге видання – К.: Освіта, 1998 – 287 с.

9. Давыдов А.С. Квантовая механика. Изд. 2-е, испр. и перераб. – М.:Наука, – 1973. – 703 с.

10. Детлаф А. А., Яворский Б. М. Курс физики: Учеб. пособие для студ. высших техн. учеб. заведений. – 4.изд., испр. – М. : Издательский центр "Академия", 2003. — 720с.

11. Зачек І.Р., Кравчук І.М., Раманишин Б.М., Габа В.М., Гончар Ф.М. Курс фізики: Навчальний підручник. – Львів: Видавництво “Бескид-Біт”, 2002 – 376 с.

12. Иродов И. Е. Квантовая физика: Основные законы: Учеб. пособие для вузов. – М.: Лаборатория Базовых Знаний, 2002. – 271с.

13. Кабардин О.Ф. Физика: Справ. материалы: Учеб. пособие для учащихся. – 3-е изд., перераб. и доп. – М.: Просвещение, 1991. – 367 с.

14. Китайгородский А.И. Введение в физику. М.: Наука. Глав. ред. физ.-мат. лит., 1973. – 688 с.

15. Корочкина Л. Н. Физика / Европейский ун-т. – К. : Издательство Европейского университета, 2006. – 217с.

16. Коршак Є.В. та ін. Фізика, 11 кл.: Підруч. для загальноосвіт. навч. закл./ Є.В. Коршак, О.І. Ляшенко, В.Ф. Савченко. – К.; Ірпінь: ВТФ “Перун”, 2004. – 288 с.

17. Куліш В. В., Соловйов А. М., Кузнєцова О. Я., Кулішенко В. М. Фізика для інженерних спеціальностей. Кредитно-модульна система: Навч. посібник для студ. вищ. навч. закладів:У 2 ч. – Ч. 2 – К. : НАУ, 2004. – 380с.

18. Кучерук І.М., Горбачук І.Т. Загальний курс фізики: У 3 т.: Навч. посіб. Для студ. вищ. техн. і пед. закл. освіти / З ред. І.М. Кучерука. – К.: Техніка, 1999. – Ч.3, С. 247.

19. Левич В.Г., Вдовин Ю.А., Мямлин В.А. Курс теоретической физики, т. 2, М.: Наука. Глав. ред. физ.-мат. лит., 1962. – 820 с.

20. Матвеев А.Н. Атомна фізика: Учеб. Пособие для студентов вузов. – М.: Высш. шк., 1989. – 432 с.

21. Мякішев Г.Я., Буховцев Б.Б. Фізика: Підруч. для 11 кл. серед. шк. – 2-ге вид. – К.: Освіта, 1993. – 272 с. :іл., с.184.

22. Сивухин Д.В. Оптика: Учеб. пособие. – 2-е изд., испр. – М.: Наука. Гл. ред. физ.-мат. лит., 1985 – 752 с.

23. Сивухин Д.В. Атомная и ядерная физика: Учеб. пособие. В 2-х ч. Ч.1. Атомная физика. – М.: Наука. Гл. ред. физ.-мат. лит., 1986 – 416 с.

24. Спроул Р. Cовременная физика. Изд. второе, переработанное. Перевод с англ, под ред. В.И. Когана. Серия «Физико-математическая библиотека инженера», Глав. ред. физ.-мат. лит. изд. «Наука», М., 1974 г. – 592 с.

25. Типлер П.А., Ллуэллин Р.А. Современная физика: в 2 т.:пер. с англ. – М.: Мир, 2007. – Т. 1. – 494с.

26. Троицкая В. В., Цапко Т. П. Физика: Учебник для студ. вузов / Национальный фармацевтический ун-т. Ч. 2. – Х. : Издательство НФаУ "Золотые страницы", 2006. – 216с.

27. Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике, Т.3. Излучение. Волны. Кванты. М.: Издательство “Мир”, 1976 – 496 с.

28. Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике, Т.9. Квантовая механика. М.: Издательство “Мир”, 1976 – 528 с.

29. Фриш, С.Э. Курс общей физики (Классическая учебная литература по физике): Учебник: в 3 т. Т. 3. Оптика. Атомная физика/С. Э. Фриш, А. В. Тиморева. – Изд. 8-е, стереотип. – СПб.: Лань, 2006. – 648 с.

30. Чолпан П. П. Фізика: Підручник для студ. природничих ф-тів ун-тів і пед. ін-тів. – К.: Вища школа, 2003. — 567с.

31. Шкилько А. М., Рудакова Г. А. Физика: Учеб. пособие / Украинская инженерно-педагогическая академия. — Х. : УИПА, 2005. — 428с.

32. Шпольский Э.В. Атомная физика. т. 1. Введение в атомную физику. – М.: Наука, 1974. – 576 с.

33. Яворский Б.М.,Пинский А.А. Основы физики. т. 2. Электродинамика колебания и волны основы квантовой физики атомов, молеккул и твердых тел физика ядра и элементарных частиц.-М.: Наука, 1972. – 732 с.

34. Max Born. Atomic physics. Blackie and son limited, London - Glasgow, 1963-490p. Перекл.: Макс Борн. Атомная физика, М.: Мир, 1965 – 484 с.

35. R.H. Pantell, H.G. Puthoff. Fundamentals of quantum electromics. John Willey inc, N.Y., 1969 – 380 p. Перекл.: Р. Пантел, Г. Путгоф. Основы квантовой электроники, М.: Мир, 1972 – 384 с.