ФИЗИКА/ 2.Физика твердого тела.

Захарченко Р.В.^1,2, Воробйов Ю.В.²

¹Національний технічний університет України «КПІ», Україна

²Лабораторія дослідження матеріалів при Національному політехнічному інституті Мексики, відділення Керетаро, Мексика

Оптимізація будови фотоелектричної панелі для гібридної ФЕ/термічної системи

Вступ. Комбінований фотоелектричний (ФЕ) – термічний колектор (в літературі його часто називають як комбі-панель /combi-panel/) досить ретельно як теоретично, так і практично досліджується з приблизно 1978 року (див. наприклад [1, 2-7]). Така гібридна система має явні переваги над її окремими складовими: вона виробляє більше енергії на одиницю площі аніж отримана енергія з поокремим використанням фотоелектричної панелі (ФЕП) та сонценагрівної колекторної панелі. Охолодження ФЕП водяним або повітряним теплоекстрактором (тепловідводом) підвищує його електричну ефективність. Деякі з систем подібного типу вже мають промислову стадію розробки, хоча наразі вони досить дорого коштують. В усіх процитованих роботах передбачається, що обидві панелі в системі мають однакову площу. Але ми маємо іншу точку зору. Очевидно, що наявність ФЕП над сонценагрівним колектором (СНК) зменшує тепловий потік до останнього, що, в свою чергу, зменшує термічну ефективність колектора. З іншого боку, спроможність колектора екстрагувати тепло від ФЕП зменшується коли вода (повітря) всередині нього нагрівається. Тому, оптимальним варіантом буде зробити ФЕП меншої площі аніж площа нагрівного колектора під нею, і розмістити ФЕП поблизу початкової частини колектора (де знаходиться втік холодної води), щоб забезпечити більш ефективне охолодження ФЕП та підвищити ефективність нагрівного колектора.

Далі ми обсудимо проблеми оптимізації співвідношення між площами двох частин досліджуваної гібридної системи та розглянемо як можна оптимізувати будову ФЕП для такої системи. Також зробимо загальний теоретичний розгляд та представимо результати експериментального вивчення системи з різними ФЕП; а зроблені нами рекомендації стосуються матеріалів та дизайну оптимізованих ФЕП, прототип якої був нами сконструйований і досліджений.

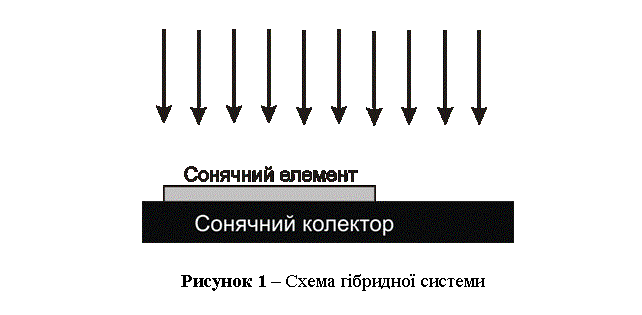Загальний розгляд. Щоб отримати просту модель даної системи ми проаналізували пристрій, зображений на рис. 1. На рисунку ми розмістили ФЕП (на рисунку позначена як ”Сонячний елемент”) з площею поверхні А_р над СНК (на рисунку позначена як “Сонячний колектор”) з загальною площею А_с таким чином, що ФЕП покриває частину СНК, суміжну з його вхідною областю. Позначимо через G інтенсивність сонячного випромінювання (тобто його потужність на одиницю площі). Нехай η буде ефективністю перетворення світлової енергії в електричну в нашій ФЕП, R – коефіцієнт відбивання ФЕП (зазвичай напівпровідникова панель має відчутний коефіцієнт відбивання оскільки напівпровідниковий матеріал має високе значення коефіцієнта заломлення світла, в той час як СНК будемо вважати чорним і тому з гарним наближенням взагалі не відбиваючим світло).

Тоді теплова потужність, що генерується в межах ФЕП, знову ж таки на одиницю площі, може бути записана за допомогою виразу

Ця потужність передається (головним чином завдяки процесу теплопровідності з ефективністю η_с приблизно рівною 0.5÷0.7, що є характеристикою СНК) до СНК; тоді вся теплова енергія, отримана тепловим колектором буде

Тут ми для спрощення вважаємо, що ефективність колектора однакова для його частини на сонячному світлі та частини, покритої ФЕП: взагалі то кажучи, ефективність різна в цих двох частинах, але експерименти (див. нижче) не призводять до обговорення цієї відмінності. Отож, з таким наближенням ми отримуємо ефективне значення коефіцієнта корисної дії (к.к.д.) η_с^* нашого СНК обговорюваної гібридної системи у вигляді

Електрична ефективність ФЕП зазвичай складає від 10 до 20%; коефіцієнт відбивання має той самий порядок коли використовують антирефлекторне покриття, інакше він може бути 30 ÷ 35%. Тому коефіцієнт (R + η – Rη) в (3) приймає значення в межах 0.2 ÷ 0.6, що може призвести до серйозного зменшення термічної ефективності СНК коли відношення площ наближається до 1. Щоб вплив цього ефекту був нехтовно малим, необхідно тримати це співвідношення значно меншим за 1. В наших експериментах для цього співвідношення ми дотримувались умови А_р/А_с ≤ 0,25. Також з вище наведених міркувань очевидно, що втрати термічної енергії, накопиченої в СНК, обумовлені наявністю ФЕП поверх нього, і ці втрати не компенсуються електричною енергією, що виробляється ФЕП. Останню можна описати за допомогою виразу W_e = G(1 – R)ηA_p, що дає нам наступний вираз для загальної (теплова + електрична) енергії, яка виробляється гібридною системою:

Видно, що для типових значень параметрів, наданих вище, ця енергія завжди менша аніж енергія вироблена ізольованою СНК (Gη_cA_c), хоча і може наближатись за своїм значенням до неї.

Додатковим моментом на користь нашого висновку про необхідність малого значення відношення А_р/А_с, як умови для вищої ефективності гібридної системи, є внесок температурного розподілу вздовж СНК. Це очевидно (і може бути показано, як розрахунками, так і експериментально), що температура СНК, експонованого на сонячному світлі, поступово зростає від граничної області входу в колектор холодної води (у даному випадку ця температура практично дорівнює температурі навколишнього середовища) до свого максимального значення на протилежному кінці колектора. Тому, збільшення площі перекриття фотоелектричною панеллю сонценагрівного колектора буде зменшувати ефект охолодження панелі, таким чином виключаючи головну перевагу комбінації цих двох пристроїв в одну гібридну систему.

Для описання теплового перерозподілу в часі між ФЕП та СНК ми вважатимемо, що тепловий взаємообмін починається в момент часу t = 0, тоді рівняння теплової рівноваги для ФЕП можна записати в наступному вигляді:

де С = P_p/cm, та В = A_p(k^*/d^* + h)/cm; P_p визначається (1), ΔT це різниця температур між ФЕП та оточуючим середовищем, “c” це питома теплоємність ФЕП, “m” – її маса, k^* та d^* – ефективні теплопровідність та товщина поверхні розподілу між ФЕП та СНК, “h” це коефіцієнт теплових втрат у повітря біля експонованої сонячним світлом поверхні ФЕП (залежить від конвекційних умов, наявності вітру, і т.д., але було прийнято до розгляду його деяке середнє значення). Ми повинні також звернути увагу на те, що рівняння для теплового потоку через межу розподілу ФЕП–СНК може містити не ΔT, а різницю температур між двома панелями ΔT^*, але оскільки ми використовуємо ефективні значення параметрів, що характеризують цю границю розподілу, то і різниця між ΔT та ΔT* буде поглинута цими ефективними параметрами.

Додаючи умову (5) та використовуючи початкові умови (ΔT = ΔT_о для моменту часу t = 0), ми отримаємо закон експоненційного загасання з часом

де ΔT_∞ це кінцева різниця температур, яка дорівнює

Експериментальне дослідження ФЕ/термічної системи з різними комерційними моделями ФЕП. Ми використовували модель СНК (model Powermat) площею 4 м², в якій нагрівним агентом була вода; приблизно 90% площі поверхні контролювалося системою внутрішнього трубопроводу, який забезпечує ефективний тепловий взаємообмін. Чорний ФЕП поглинач, який покриває колектор є стійким до ультрафіолетової частини сонячного спектру і має гарантійний термін експлуатації приблизно 20 років; це також забезпечує невелику вагу панелі (приблизно 3 кг в незаповненому стані, та 5 кг в наповненому водою стані). Максимальна оціночна теплова ефективність при використанні моделі Hottel-Whillier (Hottel-Whillier model) [2], була в межах 60÷70%, що відповідає найкращим з відомих колекторів.

В експериментальній гібридній системі використовувались та досліджувались ФЕП, збудовані на основі кремнію кристалічного типу (c-Si; зокрема, ми використовували панель виробництва російського заводу “Красное знамя” з площею приблизно 1 м² та генерованою потужністю 100 Вт). Між іншим, в наших експериментах для досягнення ефективного термічного контакту з колектором ми використовували панелі, зроблені з аморфного кремнію (α-Si, ECD Company, Troy, Michigan, USA) та CuInSe₂ (CIS) комерційні панелі виготовлені компанією Siemens, USA. Електрична ефективність усіх використаних ФЕП була приблизно 15%. Фото останньої моделі ФЕП, розміщеної поверх СНК зображене на рис. 2.

Установка, розроблена для дослідження режиму сонячного колектора, включала в себе два саморобних електричних цифрових термометри на базі температурних сенсорів LM335 та вимірювач водяного потоку (water flux meter CICASA Delaunet MD-15); усі три пристрої були приєднані до комп’ютеризованої системи збору даних.

Ефективність колектора визначали за допомогою добре відомого виразу

де m_t це потік води (маса за секунду), c_c – питома теплоємність води, T_o – вихідна температура води і T_e – температура води на вході в колектор.

На рис. 3 зображена залежність ефективності СНК від різниці температур води, що входить до колектора і температури навколишнього середовища Т_а. Залежність майже лінійна, що добре погоджується з моделлю Hottel-Whillier, а максимальне значення ефективності наближається до значення 70%, що, в свою чергу, вказує на чудові експлуатаційні якості даного колектора. Експерименти були проведені з різноманітними сонячними елементами на поверхні колектора (усі вони мали площу не більшу за 1 м²) і при цьому жодної зміни в ефективності не було виявлено, що і очікувалось з вищенаведеного аналізу.

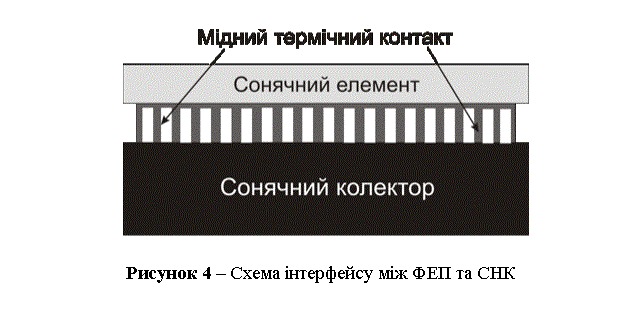
Для забезпечення найкращого можливого теплового контакту між панеллю та колектором ми робили для кожного випадку спеціальний інтерфейс у вигляді мідного радіатора, притиснутого до ФЕП (прямо до матеріалу підкладки з неосвітленого боку сонячних елементів) та до сонячного колектора з іншого боку, як це показано на рис. 4. Теплопровідність k радіатора була визначена експериментально: ми привели радіатор до термічного контакту з 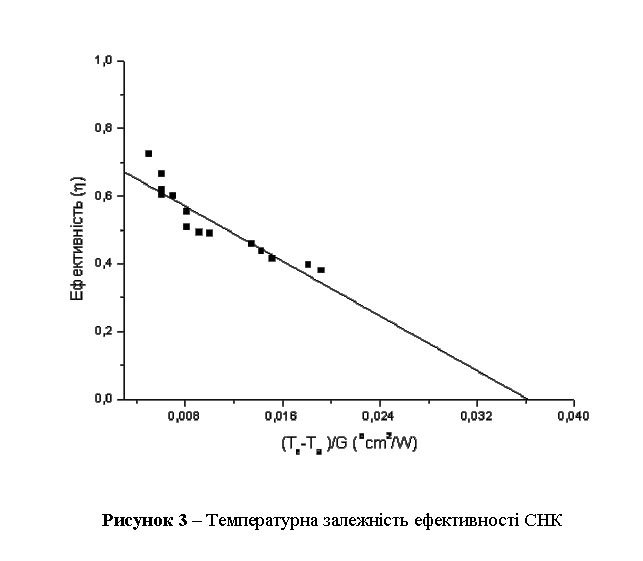алюмінієвою пластиною в певному сенсі щоб гарантувати однаковий тепловий потік через пластину і радіатор, та заміряли зовнішні температури так само, як і температуру в області контакту. Прирівнявши вирази для двох теплових потоків, ми отримуємо провідність невідомого матеріалу. Значення k, отримане таким чином, дорівнювало 190 Вт/(м·К), що досить багато (воно лише у два рази менше ніж теплопровідність Cu, і наближається до значення “k” для Al).

Щоб знайти ефективну теплопровідність в приконтактній області, нам необхідно знати коефіцієнт “h” в формулі (5). Для цього ми беремо середнє експериментальне значення різниці температур між ФЕП, експонованої на сонячному світлі, але без термічного контакту з СНК, та температури навколишнього середовища (30 К), і користуємось для розрахунків виразами (7) вважаючи, що k^* = 0. Така підстановка дає нам значення h = 20 Вт/(м²·К). Беручи для подальшої оцінки якості термічного контакту експериментальне значення фінальної різниці температур між панеллю та колектором у випадку CIS панелі ΔT_∞ = 10 К, фактичну товщину інтерфейсу 2 см та використовуючи вираз (7) із вже знайденим значенням “h” ми оцінили ефективну теплопровідність термічного контакту як k ≈ 1 Вт/(м·К). Таке значення показує, що конструкція панелі не відповідає адекватному взаємному теплообміну між панеллю та сонячним колектором (приблизно таке ж саме значення “k” ми отримали з виразів (7) беручи для розрахунків час релаксації, експериментальне значення часу релаксації складає приблизно 5 хв.).

Висновки. З описаних експериментів ми приходимо до висновку, що конвекційні ФЕП не є адекватними для їх використання в гібридних ФЕ/термічних системах; вони не забезпечують ефективного відбору з них тепла сонценагрівним колектором, тож охолодження не ефективне (наші експерименти показали збільшення ефективності ФЕП за рахунок термічного контакту з СНК не більше ніж на 0,5%). Таким чином, однією з головних вимог до конструкції ФЕП є забезпечення найкращого з можливих термічних контактів з СНК; таку вимогу можна задовольнити відповідним вибором підкладки матеріалу ФЕП.

Література:

1. Kern Jr., E. C. Combined photovoltaic and thermal hybrid collector systems [Текст] / E. C. Kern Jr., M. C. Russel // Proceedings of the 13^th ISES Photovoltaic Specialists, Washington, DC, USA. – 1978. – P. 1153-1157.

2. Florshuetz, L. W. Extension of the Hottel-Whillier model to the analysis of combined photovoltaic/thermal flat plate collectors [Текст] / L.W. Florshuetz // Sol. Energy. – 1979. - Vol. 22. – P. 361-366.

3. Raghuraman, Р. Analytical predictions of liquid and air photovoltaic/thermal flat plate collector performance [Текст] / P. Raghuraman // J. Sol. Energy Eng. – 1981. – Vol. 103. – P. 291-298.

4. Thomas, H. P. PV and PV/Hybrid products for buildings [Текст] / H.P. Thomas, S.I. Hayter, R.I. Martin, L.K. Pierce // Proceedings of the 16th European PV Solar Energy Conference, Glasgow, UK. – 2000. - Vol. II. - P. 1894-1897.

5. Bharava, A. K. Study of a hybrid solar system—solar air heater combined with solar cells [Текст] / A. K. Bharava, H. P. Garg, R. K. Argaval // Energy Conversion and Management. – 1991. – Vol. 31. – Issue 5. – P. 471-479.

6. Tripanagnostopolus, Y. Hybrid photovoltaic/thermal solar systems [Текст] / Y. Tripanagnostopolus, Th. Nousia, M. Souliotis, P. Yanoulis // Sol. Energy. – 2002. - Vol. 72. – Issue 3. – P. 217-234.

7. Zondag, H. A. The thermal and electrical yield of a PV-thermal collector [Текст] / H. A. Zondag, D. W. De Vries, W. G. Van Helden, R. J. C. van Zolingen, A. A. van Steenhoven // Sol. Energy. – 2002. - Vol. 72. – Issue 2. – P. 113-128.