Технические науки / 11. Робототехника

К.т.н. Колдаев В.Д.

Национальный исследовательский университет МИЭТ, Россия

Использование графовых моделей для сегментации изображений

В процессе развития систем обработки изображений появилось несколько концепций и подходов к представлению изображений и большое количество структур данных для реализации этих представлений. При позиционном представлении плоскость изображения разбивается с помощью прямоугольной сетки на элементы одинакового размера (квадраты), которые для рассматриваемого приложения являются наименьшими неделимыми частями изображения. При структурном описании изображения исходят из предпосылки, что изображение можно представить набором объектов, объект – набором некоторых базисных элементов, базисные элементы – набором графических примитивов, а также набором отношений внутри каждой группы этих компонентов, задающих их упорядоченность. Объединение представлений может быть выполнено на уровне одной структуры или с помощью организации двух баз данных изображений и связей между ними.

Среди алгоритмов контурной сегментации особое место занимают алгоритмы обработки изображений, основанные на представлении сегментов изображения в виде графа и поиске на графе пути наименьшей стоимости, который соответствует значимым контурам. Для структурного описания изображения, инвариантного относительно операций переноса и поворота, используется граф с помеченными вершинами и ребрами. Процедура распознавания состоит в установлении изоморфизма графов описания исходного и заданного эталонного изображения [1].

Важным подходом для описания вида структуры плоской области является ее представление в виде графа. Во многих случаях для этого определяется остовное дерево (скелет) области с помощью прореживающих (сокращающих) алгоритмов. В графе может существовать вершина, называемая точкой сочленения (разделяющей вершиной), удаление которой вместе с инцидентными ей ребрами разъединяет оставшиеся вершины. На рис.1 точками сочленения являются вершины с номерами 4, 5 и 7.

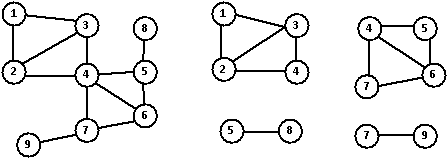
Рис.1. Разделимый граф и его двусвязные компоненты

Максимальный двусвязный подграф (без точек сочленения) является двусвязной компонентой или блоком [1]. Каркас (V, T) связного неориентированного графа G = (V, E) содержит (N – 1) ребро, где N – количество вершин G. Каждое ребро, не принадлежащее T, т.е. любое ребро из (E – T), порождает в точности один цикл при добавлении его к T. Поскольку каркас состоит из (N – 1) ребра, в фундаментальном множестве циклов графа G относительно любого каркаса имеется (M – N + 1) циклов, где M – количество ребер в G. Для нахождения контурного каркаса (стягивающего дерева) графовой структуры используются методы поиска в глубину и в ширину. При поиске в глубину анализируется вершина u, смежная с v. Если на очередном шаге у вершины q нет вершин смежных с ней и не рассмотренных ранее, то осуществляется возврат из вершины q к вершине, которая была до нее. При поиске в ширину на каждом шаге рассматриваются все вершины, связанные с текущей [2].

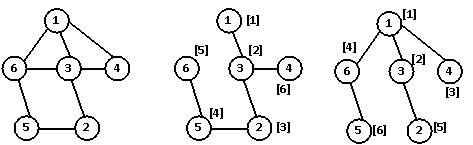
Граф и его каркасы, построенные методами поиска в глубину и в ширину, показаны на рис.2 (в скобках указана очередность просмотра вершин графа). При использовании графовых структур часто применяют методы, основанные на определении однородных цветов или текстур, либо метод водоразделов. В работе для контурной сегментации изображений предлагаются алгоритмы построения ациклических подграфов: Крускала, Прима, Дейкстра [3].

а б в

Рис.2. Граф (а) и его контурные каркасы, построенные методами поиска

в глубину (б) и в ширину (в)

Пусть – вершина графа градиентного изображения, тогда существует вершина , принадлежащая контурному изображению, причем вершина V₁ принадлежит окрестности точки V₂. Введем числовую характеристику , которую будем называть стоимостью вершины графа градиентного изображения, а – функцией модуля градиента изображения. Далее рассмотрим две вершины V₁ и V_k и предположим, что эти вершины принадлежат контуру. Очевидно, что любой путь, соединяющий данные вершины можно рассматривать в качестве аппроксимации данного гипотетического контура. Длиной (стоимостью) пути

(V₁, V₂, ..., V_m, V_k ) будет сумма .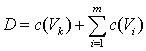

Наиболее точной аппроксимацией контура (кривой), соединяющей вершины V₁, V_k будет путь, имеющий наименьшую стоимость. С учетом этого можно сформулировать следующую оптимизационную задачу выбора контурного изображения. Наиболее оптимальное контурное изображение является частичным подграфом градиентного изображения, который имеет наименьшую стоимость из всех допустимых подграфов. Стоимость подграфа определяется как сумма стоимостей его вершин. Расстоянием между вершинами V₁ и V₂ на графе градиентного изображения называется стоимостью пути, соединяющего эти вершины [3]. Аналогичным образом определяется расстояние на графе контурного изображения. Для того чтобы графы контурного и градиентного изображения имели приблизительно одинаковые метрические характеристики, необходимо, чтобы расстояние, вычисляемое по графу контурного изображения, было приблизительно такое же, как и на графе градиентного изображения, т.е. для вершин V₁,V₂ контурного изображения. Для всех пар (V₁, V₂) близко расположенных вершин , , удовлетворяющих условию: , необходимо проверить справедливость неравенства . Если это неравенство не выполняется, то для каждой такой пары вершин (V₁, V₂) необходимо построить путь, имеющий наименьшую стоимость и соединяющий вершины V₁ и V₂ , и добавить вершины, принадлежащие этому пути, к графу G_c.

Задачи распознавания видеоизображений связаны с вводом, фильтрацией, выделением контуров, выбором системы признаков, сегментацией и поиском оптимальных алгоритмов принятия решения.

Литература

1. Колдаев В.Д. Контурное представление изображений в автоматизированных производственных системах [Текст] / В.Д. Колдаев, А.А. Шебек // Сборник материалов 3-й международной научно-практической конференции «Наука и устойчивое развитие общества. Наследие В.И. Вернадского». – Тамбов, 2008. – С. 220-222.

2. Колдаев В.Д. Алгоритмы построения покрывающего дерева сети [Текст] / В.Д. Колдаев // Информатика и управление: Межвузовский сборник / Под ред. д.т.н., проф. В.А. Бархоткина. – М.: МИЭТ, 2005. – С. 72-77.

3. Колдаев В.Д. Графовые модели контурной сегментации изображений [Текст] / В.Д. Колдаев // Сборник научных трудов «Моделирование, алгоритмизация и программирование при проектировании информационно-управляющих систем». Под ред. д.т.н., проф. В.А. Бархоткина. – М.: МИЭТ, 2008. – С. 255-260.