Технические
науки/2. Механика.
к.ф.-м.н.,
доцент Нуримбетов А.У., Туреханова Г.И., Жанбосынов Р.С.
Таразский государственный университет им. М.Х. Дулати, Казахстан
Основные соотношения
динамической упругости армированного слоистого стержня с переменными
физико-геометрическими параметрами
Используемые в
практической деятельности человека материалы, как правило, неоднородны. В таких
материалах, как металлические сплавы, характерный размер неоднородности (d) мал по сравнению
расстояниями (L), характеризующими "неоднородность"
деформации (L>d). Для композицион-ных материалов (КМ),
полученных армированием материала матрицы волокнами наполнителя, характерный
размер (![]() ) неоднородности структуры (например, толщина слоя,
обусловленная диаметром волокна d1), намного больше, чем для
металлических сплавов (
) неоднородности структуры (например, толщина слоя,
обусловленная диаметром волокна d1), намного больше, чем для
металлических сплавов (![]() >d1»d). Поэтому возможны такие условия
динамического нагружения композиционных тел, когда характерный размер
"неоднородности" деформации (L) не сильно превышает характерный размер
"неоднородности" структуры (
>d1»d). Поэтому возможны такие условия
динамического нагружения композиционных тел, когда характерный размер
"неоднородности" деформации (L) не сильно превышает характерный размер
"неоднородности" структуры (![]() ). Структурная теория армированных сред [1] позволяет
описать такие деформации (L>
). Структурная теория армированных сред [1] позволяет
описать такие деформации (L>![]() >d1) если эти размеры обеспечивают справедливость
осреднения параметров по фазам композиции [3], т.е. они отличаются хотя бы на порядок. В первой части данной работы получены основные вариационные
принципы связанной и несвязанной упругости армированного слоистого тела в
условиях динамического деформирования. Во второй части работы исследованы свободные изгибные колебания армированных
слоистых стержней. При этом рассмотрены
два случая: разность смещений компонентов слоев ничтожно мала, смешения таковы,
что нельзя пренебречь их.
>d1) если эти размеры обеспечивают справедливость
осреднения параметров по фазам композиции [3], т.е. они отличаются хотя бы на порядок. В первой части данной работы получены основные вариационные
принципы связанной и несвязанной упругости армированного слоистого тела в
условиях динамического деформирования. Во второй части работы исследованы свободные изгибные колебания армированных
слоистых стержней. При этом рассмотрены
два случая: разность смещений компонентов слоев ничтожно мала, смешения таковы,
что нельзя пренебречь их.
Во втором случае получен
качественно новый результат. Численный анализ простейших случаев показывает
удовлетворительное совпадение собственных частот с опытными данными.
1. Основные
соотношения динамической упругости армированных тел.
При нестационарном деформировании армированных слоистых сред движение их
элементарного объема описывается уравнениями
![]() (1)
(1)
здесь![]() , причем ρi - плотности материала слоя и Vi объемное содержание материала слоя i.
, причем ρi - плотности материала слоя и Vi объемное содержание материала слоя i.
Соотношения между напряжениями ![]() и деформациями
и деформациями ![]() для слоя i определяются
из формулы
для слоя i определяются
из формулы
![]() . (2)
. (2)
Параметры ![]() являются
характеристиками упругости,
являются
характеристиками упругости, ![]() ,
, ![]() температура и тензор
тепловых расширений i-го слоя КМ [2].
температура и тензор
тепловых расширений i-го слоя КМ [2].
При "обобщенном
" кручении компоненты перемещения точек i-го слоя отыскивается в виде
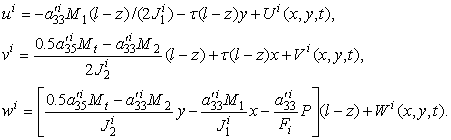 (3)
(3)
Здесь ![]() некоторые подлежащие определению функции координат
сечения х, у, t; t - относительный угол
закручивания на единицу длины стержня;
некоторые подлежащие определению функции координат
сечения х, у, t; t - относительный угол
закручивания на единицу длины стержня; ![]() - длина стержня;
- длина стержня; ![]()
![]() (k=1,2)
- главные моменты инерции поперечного сечения i-го слоя;
(k=1,2)
- главные моменты инерции поперечного сечения i-го слоя; ![]() =
=![]() - площадь сечения i-го слоя;
- площадь сечения i-го слоя; ![]() - силы и моменты, действующие в поперечном сечении стержня.
- силы и моменты, действующие в поперечном сечении стержня.
Если подставить
соотношение (2) в выражения (1), то получатся уравнения движения
армированной среды в перемещениях:
В
этих формулах точка над переменной величиной означает дифференцирование по
времени, как и прежде k,
j,m,n=1,2,3. Система трех уравнений (2) содержит в качестве
неизвестных 4 переменных: 3 смещений и температуры Тi. Для замыкания системы
необходимо добавить уравнения теплопроводности армированной среды [ ]:
![]() (5)
(5)
Здесь wi - члены, характеризующие внутренние источники
тепла; ![]() - постоян-ные
по величине компоненты симметричного тензора теплопроводности;
- постоян-ные
по величине компоненты симметричного тензора теплопроводности; ![]() - коэффициенты теплоемкостей материала слоя при постоянной
деформации; Тi
- начальные температуры материалов слоя i.
- коэффициенты теплоемкостей материала слоя при постоянной
деформации; Тi
- начальные температуры материалов слоя i.
Система уравнений (4) содержит температурные члены, а система
(5) - деформационные члены. Таким
образом, совокупность этих систем уравнений вместе с соответствующими граничными
и начальными условиями будет представлять собой связанную задачу динамической
упругости слоистых тел. Если система уравнений (5) не будет содержать деформационные члены, то задача становится
несвязанной. Поэтому температурные члены в правых частях уравнений (4) являются известными функциями - решением
соответствующей задачи теплопроводности.
2. Принцип виртуальных работ и основная энергетическая
теорема.
Добавим к перемещениям ![]() ,
возникшим в материалах слоя под действием изменяющихся во времени
нагрузок, виртуальные приращения
,
возникшим в материалах слоя под действием изменяющихся во времени
нагрузок, виртуальные приращения ![]() , которые предполагаются непрерывными вместе со своими
производными до второго порядка. Эти приращения являются произвольными, но
согласованными с условиями, ограничивающими деформацию тела. Например, на той
части тела, где заданы смещения, следует положить
, которые предполагаются непрерывными вместе со своими
производными до второго порядка. Эти приращения являются произвольными, но
согласованными с условиями, ограничивающими деформацию тела. Например, на той
части тела, где заданы смещения, следует положить ![]() [4]. Рассмотрим вирту-альную
работу массовых
[4]. Рассмотрим вирту-альную
работу массовых ![]() поверхностных
поверхностных ![]() сил
сил
![]() (6)
(6)
Заменяя во втором
интеграле поверхностные напряжения ![]() напряже-ниями
напряже-ниями ![]() согласно условиям краевой задачи и используя теорему
Гаусса-Остроградского, можно получить
согласно условиям краевой задачи и используя теорему
Гаусса-Остроградского, можно получить
При этом было
использовано очевидное равенство
![]() ,
,
|в котором в котором wkj - кососимметричный тензор.
Первый интеграл в (6) можно преобразовать с учетом уравнений
движе-ния (4).
Сравнение полученного результата с выражением (6) приводит к уравнению
![]() (8)
(8)
Это равенство выражает принцип
виртуальных работ динамики армированных слоистых сред, согласно которому
виртуальная работа массовых, поверхностных сил и сил инерции армированного
слоистого тела равна сумме работ сил упругого, вязкого взаимодействия
компонентов композиции на виртуальных разностях смещений и работе напряжений на
вариациях деформа-ций. Оно справедливо для упругих, так и неупругих слоистых
армированных тел, для линейных и нелинейных соотношений между напряжениями к
соответствующими деформациями.
Введение в выражении (7) физических соотношений (3)
позволяет использовать принцип для исследования линейно деформируемого
упругого армированного тела, находящегося под воздействием динамических
нагрузок. При этом тело может находиться в температурном поле, независящем от деформаций.
Предположим, что
приращения ![]() являются действительными
приращениями, т.е. справедливы соотношения
являются действительными
приращениями, т.е. справедливы соотношения
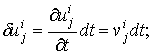 (9)
(9)
Введем следующую
величину
![]() (10)
(10)
Здесь К - кинетическая энергия армированного
слoистого тела;
Подставляя (9) в равенство (8) и используя обозначения (10),
после простых преобразований получим основное энергетическое уравнение
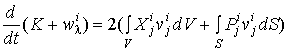 ,
,![]() (11)
(11)
Уравнения (11) выражает закон сохранения
энергии. Оно может быть использовано при доказательстве единственности решения
дифференциальных уравнений движения (4) для несвязанной задачи при
соответствующих начальных и граничных условиях.
3. Обобщенный принцип Гамильтона.
Рассмотрим непрерывно
изменяющийся во времени между моментами t=t0 и t=t1 процесс
деформирования. Приравняем действительные
перемещения ![]() к перемещениям
к перемещениям ![]() +d
+d![]() , причем варьировать будем так, чтобы
, причем варьировать будем так, чтобы
![]() (12)
(12)
Запишем принцип
виртуальных работ (8) в виде
![]() (13)
(13)
где dLi определяется
из уравнения (6).
Проинтегрируем выражение
(13) по времени от t0 до t1:
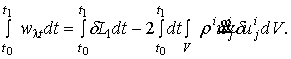 (14)
(14)
Здесь
![]() поэтому вследствие
физических соотношений (2) содержит температурные члены.
поэтому вследствие
физических соотношений (2) содержит температурные члены.
Вычислим вариацию
кинетической энергии (10)
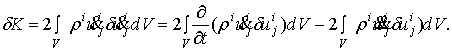
Проинтегрируем это
выражение по времени от t=t0 до t=t1. Тогда в силу предположений (12) справедливо равенство
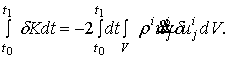
Поэтому уравнение (14) приобретает вид
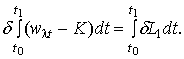 (15)
(15)
Это и есть обобщенный на слоистую среду принцип
Гамильтона. В левой части
равенства (15) знак вариации вынесен
за знак
первого интеграла по той причине, что величины ![]() , K,
являются функциями состояния - величинами, зависящими от мгновенного состояния
тела независимо от того, каким способом это состояние достигнуто. Знак вариации
d
в правой части равенства (15) можно
вынести за знак интеграла только тогда, когда внешние силы обладают потенциалом
, K,
являются функциями состояния - величинами, зависящими от мгновенного состояния
тела независимо от того, каким способом это состояние достигнуто. Знак вариации
d
в правой части равенства (15) можно
вынести за знак интеграла только тогда, когда внешние силы обладают потенциалом
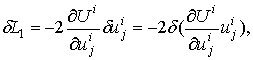
тогда
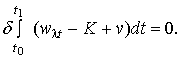
Обозначая
через П=![]() +U потенциальную энергию, получим принцип
Гамильтона в виде
+U потенциальную энергию, получим принцип
Гамильтона в виде
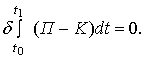 (16)
(16)
где (К-П) - функция
Лагранжа. Из (15) видно, что действие
по Гамильтону 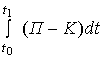 принимает экстремальное
значение, для статической задачи К=0, тогда принцип
Гамильтона сводится к принципу минимума потенциальной энергии dП=0.
принимает экстремальное
значение, для статической задачи К=0, тогда принцип
Гамильтона сводится к принципу минимума потенциальной энергии dП=0.
Полученные на основе
предложенной в [1] линейной модели нестацио-нарного деформирования слоистых
сред вариационные принципы (8) и (15) позволяют исследовать динамические
явления в армированных слоистых телах.
Литература:
1. Каримбаев Т.Д. Вариант теории армированных
сред. - Известия вузов "Машиностроение", 1975, №8.
2. Нуримбетов А.У. Решение задачи кручения слоистых композиционных
стержней произвольного сечения методом конечных элементов //Строительная
механика и расчет сооружений. М.: -
2009. -№4.- с.24-30.
3. Хорошун Л.П. К теории взаимопроникающих упругих смесей. - Прикладная
механика, 1977, Т.13, № 10, с. 124-132,
4. Новацкий В. Теория
упругости. - М.: Мир, 1975, - 872 с.