Д.т.н. Сулейменов О.А.

Таразский государственный университет, Казахстан

ПРОЦЕССЫ НА ОСАДИТЕЛЬНОМ ЭЛЕКТРОДЕ СЕПАРАТОРОВ

В коронно-электростатических барабанных сепараторах частицы, уложенные на осадительном электроде, подвергаются зарядке в поле коронного разряда, затем воздействию внешнего электростатического поля.

Частицы полуэллипсоидальной формы с полуосями b и с, объемной проводимостью γ₁ и относительной диэлектрической проницаемостью ε₁, находящиеся на заземленном осадительном электроде в поле ионизированного воздуха (γ₂, ε₂) приобретают предельный заряд /1/.

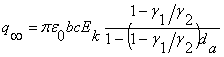(1)

где Е_к – напряженность объемного заряда.

Это выражение действительно, для случаев, когда пренебрегаем поверхностной проводимостью частицы и переходным сопротивлением в месте контакта частицы с осадительным электродом, а напряженность поля в зоне зарядки считаем равномерной.

Учитывая, что процесс зарядки определяется экспоненциальной зависимостью, для первоначальной незаряженной частицы кинетику процесса можно записать как

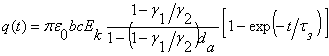(2)

Этим уравнением описывается кинетика зарядки непроводящих частиц с удельной объемной проводимостью менее 0,25×10^-9Ом^-1×м^-1 (плагиоклазы, циркон, сподумен и другие минералы).

Для диэлектриков γ₁ → 0 кинетика зарядки частицы определяется

(3)

Рассмотрим процесс разрядки частицы при мгновенном понижении напряжения с значения U₁ до U₂ (рисунок ). Причем U_нк ‹ U₁, следовательно, до момента t₁ происходит зарядка частицы в поле коронного разряда. Допустим, что к моменту t₁ частица зарядилась до значения q₁ . Затем напряжение понижается до значения U₂, которое ниже напряжения возникновения коронного разряда U_нк. Следовательно, при U₂ на частицу воздействует чисто электростатическое поле, объемный заряд исчезает. В дальнейшем происходит разрядка частицы на осадительный электрод под действием внешнего электростатического поля, созданного напряжением подпора. В данном случае напряжением подпора является U₂.

Величина и полярность индукционного заряда при отсутствии объемного заряда (g ₂ = 0) определяется согласно /1/

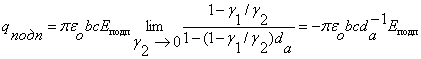(4)

где Е_подп – напряженность электростатического поля, созданного U_подп.

Кинетика разряда частицы с начальным зарядом q₁ при наличии напряжения подпора имеет вид

(5)

Подставляя значение q_подп в последнюю формулу получим зависимость при наличии напряжения подпора

(6)

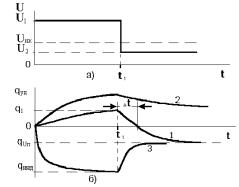
Рисунок

Высокое напряжение с прямоугольным срезом (а) и кинетика зарядки (б) частиц полупроводников (1), непроводников (2) и проводников (3)

Из последнего выражения видно, что при напряжении подпора в пределах U_нк › U_подп › 0, частица в зависимости от γ₁ может перезаряжаться, т.е. приобрести заряд противоположной полярности. А это в свою очередь сократит время, необходимое для стекания избыточного заряда на осадительный электрод Δt (рисунок ). Причем, чем выше U_подп в пределах от 0 до U_нк, тем меньше Δt .

В отличие от непроводящей и полупроводящей частицы с объемной проводимостью менее 0,25×10^-9Ом^-1×м^-1, частицы проводников (γ₁ › 0,25×10^-9 Ом^-1×м^-1) в поле объемного заряда приобретают заряд осадительного электрода, с которым они контактируют. Для проводящих частиц индукционная зарядка является преобладающей. Полярность заряда проводников противоположна полярности заряда, приобретаемого непроводниками и полупроводниками. Поэтому, согласно /1/ величина предельного индукционного заряда при γ₁ → ∞ равна

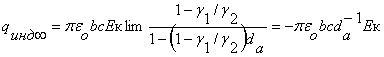(7)

Допустим, что в рассматриваемом случае постоянная времени индукционной зарядки равна постоянной времени разрядки. Тогда кинетика индукционной зарядки частицы имеет вид

(8)

В действительности значение t₃, определяемое по известной формуле для проводящей частицы, очень близко значению τ_р .

Кривая индукционной зарядки проводниковой частицы показана на рисунке (кривая 3). Скорость зарядки частиц проводниковых минералов значительно выше, чем у частиц минералов – непроводников.

Рассмотрим процесс разрядки проводящей частицы при мгновенном изменении напряжения со значением U₁ до U₂. Такой процесс рассмотрен выше для частиц непроводников (рисунок). При U₂ < U₁ происходит разрядка частицы до значения, обусловленного напряжением подпора

Кинетика разрядки частицы с начальным зарядом /q_инд / > /q_подп / согласно / 2 / имеет вид

(9)

q_инд – начальный индукционный заряд проводящей частицы.

Литература

1. И.П. Верещагин, В.И. Левитов, Г.З. Мирзабекян, М.М. Пашин. Основы электрогазодинамики дисперсных систем. М., Энергия, 1974,с. 480.

2. Мирзабекян Г.3. Зарядка аэрозолей в поле коронного разряда. В кн.: Сильные электрические поля в технологических процессах /электронно-ионная технология/. М., Энергия, 1969, с. 20-39.