Технические науки/6. Электротехника и радиоэлектроника

Тимирбекова Ж.А.

Евразийский национальный университет, Казахстан

Подходы к определению структуры телекоммуникационной сети

Быстрая эволюция телекоммуникационных технологий, обеспечивающих предоставление широкого спектра современных услуг высокого качества, обуславливает необходимость совершенствования методов проектирования телекоммуникационных сетей (ТКС), что требует системного подхода к проектированию создаваемых систем. Важнейшим этапом проектирования является выделение в создаваемой системе подсистем и определение задач, требующих решения. Среди задач, требующих решения при переходе из аналогового в цифровой формат всех видов информации – речи, данных, видео – одной из важных является задача модернизации и оптимизации структуры существующей ТКС и связанная с ней задача распределения потоков требований в сети. [1, 2].

Под структурой ТКС будем понимать совокупность ее элементов (пунктов сети) и линий связи между ними, обеспечивающих основные свойства системы – ТКС: распределение потоков требований в соответствии характеристиками ТКС, важнейшей из которых является пропускная способность линий связи.

Представим математическую модель задачи оптимизации структуры ТКС как задачу математического программирования. Математическая модель сети представляется в виде связного конечного ориентированного графа G=(А, В), где А – множество вершин графа,

поставленное в соответствие множеству пунктов i сети (i =) ; В – множество ребер графа, поставленное в соответствие множеству ветвей сети. Отметим, что ветви – это те линии связи, которые могут быть введены в ТКС, и задача состоит в том, чтобы определить необходимость их использования в соответствии с их загрузкой , которая формируется на основе получения оптимального плана распределения потоков требований в сети.

Между всеми (или некоторыми) парами пунктов i и j сети i≠j (имеется поток требований , выраженный в требуемой пропускной способности тракта передачи, используемого для раздачи программ цифрового эфирного вещания, мультимедийного трафика и др.

Для распределения каждого потока требований в сети определяются пути,

(),

где – множество возможных путей распределения потока требований _;

- ν-ый путь множества ; ν=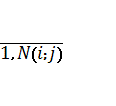, N(i, j) – количество путей множества .

Каждая ветвь сети (x,y=), x≠y характиризуется: заданной максимально возможной пропускной способностью ; показателем надежности ; достоверностью передаваемой информации ; длиной , определяемой географическим расстоянием между пунктами x и y; велечиной нагрузки , определяемой суммарной величиной передаваемых по ветви требований , пути передачи которых включает ветвь :

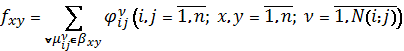
Величина нагрузки определяется в рзультате распределения потоков требований (). Здесь - часть требования , для распределения которого используется путь . Используются и другие характиристики.

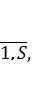В соответствии с этим пути, образуемые ветвями, также характеризуется показателями, определяемыми характеристиками ветвей, составляющих путь. При этом параметр пути , характеризующий качество обслуживания потока в сети по данному пути, определяется частичными критериями - функциями от выбранного пути, где s – номер частичного критерия, s= – количество частичных критериев, характеризующих качество обслуживания. Поскольку значение каждого из частичных критериев определяется характеристиками ветвей, составляющих путь, имеем:

(, …) (1)

Как отмечалось, основными характеристиками путей являются пропускная способность , определяемая пропускная способность ветвей , составляющих путь, ранг , показатели надежности и достоверности передаваемой информации по пути , длина и др. [1,3]. Под рангом пути понимают количество ветвей сети, составляющих путь. Таким образом, выражение (1) может быть представлено в виде:

() (2)

Зависимость параметра пути от величины загрузки ветвей , образующих путь , будем понимать в том смысле, что чем выше значение ветвей , образующих путь , тем более высокую пропускную способность соответствующих ветвей сети предполагается использовать для обслуживания потоков, что приводит к повышению качества обслуживания потока в сети.

С учетом того, что все значения определяется характеристиками ветвей , составляющих путь, выражение (2) может быть записано в виде:

() (3)

- количество ветвей, составляющих путь .

Таким образом, среди всех возможных путей распределения потоков требований в сети необходимо использовать пути максимально возможной пропускной способности ветвей, образующих пути, минимально возможного ранга, максимально возможных надежности и достоверности передаваемой информации, минимально возможной длины [3].

Отметим также, что для оценки качества обслуживания по выбранному пути распределения потоков требований могут быть использованы и другие критерии.

Задача определения оптимального плана распределения потоков требований на раздачу необходимой нагрузки по критерию гарантированного качества обслуживания формулируется следующим образом.

На множестве {M} планов M={M₁, M₂, M₃,…} (возможных структур ТКС с распределением потоков требований), в котором каждому плану поставлено в соответствие значение К – критерия оптимальности плана K{M}=K{M₁, M₂, M₃,…}, найти план, которому соответствует гарантированное качество обслуживания потоков требований в сети:

(4)

где , - количество путей множества , при ограничениях:

1) 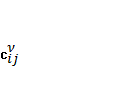≥0,

2) суммарная пропускная способность 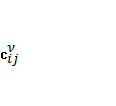всех путей, используемых для распределения потока требований , должна по возможности равняться величине этого требования:

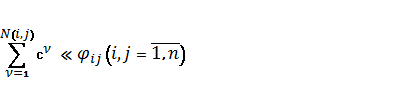(5)

где - число используемых путей для распределения потока требований ;

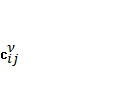- пропускная способность ;

3) суммарная пропускная способность путей всех потоков требований, проходящих по ветви , не должна превышать предельной пропускной способности этой ветви:

(6)

Отметим, что выражение (3) показатель - это качество обслуживания части потока требований , зависящее от выбранного пути распределения потока .

Для определения качества обслуживания части требования по пути вводится скалярная аддитивная функция полезности:

(7)

где - частичный критерий, характерезующий качество обслуживания по пути (пропускная способность, ранг и др.); - весовые коэффициенты частичных критериев, характерезующие их значимость, причем =1; S – количество используемых частичных критериев.

Для определения значений коэффициентов частичных критериев используем экспертные оценки приоритета частичных критериев [2] и сформируем матрицу приоритетов. По матрице приоритетов сформируем систему уравнений, решив которую, определим значения весовых коэффициентов [1].

Покажем, как формируется матрица приоритетов для данных частичных критериев. Их порядковый номер сответствует последовательности (2). Кроме того, будем считать, что последовательность частичных критериев выстроена в соответствии с их значимостью, а именно: в данном примере наибеольшей значимостью обладает параметр пути , зависящий от величины загрузки ветвей , затем – ранг , надежность пути и достоверность передаваемой информации по пути , длина пути.

Пусть значимость (приоритет) первого частичного критерия – величины загрузок ветвей -более значимости второго частичного критерия – ранга пути и экспертная оценка приоритетов =5/1. Аналогично, на основании экспертных оценок, имеем: =8/1, …, =5/1 и т.д. На пересечении второй строки первого столбца записываем «1» и т.д. значения диагональных элементов устанавливаем в нуль. Последний столбец содержит сумму элеметов строки. Матрица приоритетов для рассматриваемых в примере частичных критериев и используемыми экспертными оценками представлена в табл. 1.

Табл.1

	0	5	8	8	10	31
	1	0	5	8	10	24
	1	1	0	5	8	15
	1	1	1	0	5	8
	1	1	1	1	0	4

Для определения весовых коэффициентов , , , , имеем систему уравнений [1]:

= ; =; = и т.д., + + + +=1

Результирующий скалярный критерий для рассмотренного в табл. 1 примера можно представить следующим образом:

= 0,378+0,292+0,183+0,098+0,049 (8)

где - некоторое нормированное значение ^fxy;- некоторое нормированное значение ^Rij; - некоторое нормированное значение ^Pij; - некоторое нормированное значение ^Dij; - некоторое нормированное значение ^Lij.

Для нормирования показателей целесообразно пользоваться выражением [1]:

=/, s=

где - некоторое опорное значение частичного критерия ;

S – количество используемых частичных критериев, в данном случае S=5.

При использовании скалярной аддитивной функции полезности (взвешенной сумы (7)) в качестве опорных значений целесообразно выбирать их предельно допустимые значения, поскольку при этом нормированное значение характерезует отклонение в значении частичного критерия сравнительно с его предельно допустимым значением.

Матрица приоритетов (табл. 1) строится либо для каждого множества путей (i, j= ) исходя из экспертных оценок [2].

Для приведенного в табл. 1 примера результирующий скалярный критерий, характерезующий качество обслуживания требования , распределение которого осуществляется с использованием пути , будет иметь вид:

= 0,378 + 0,292 + 0,183 + 0,098 + 0,049 (9)

Задача в постановке (4) при ограничениях (5) и (6) представляет задачу распределения в сети многопродуктового потока, которая формируется как задача дискретного математического программирования. Для решения задач такого класса в сетях большой размерности целесообразно проводить разработку эвристических алгоритмов, основанных на использовании методов параллельного ил последовательного распределения потоков требований, итерационных процедур получения плана распределения с последующим улучшением плана и т.д. Очевидно, что степень приближения полученного решения задачи (4) с ограничениями (5) и (6) к оптимальному решению определяется эффективностью используемых алгоритмов.

Разработанный алгоритм основан на формировании последовательности планов распределения потоков требований на сути, сходящейся с заданной точностью к оптимальному в смысле критерия (4) плану. Суть алгоритма сводится к следующему.

1) Предварительное ранжирование потоков требований для определения очередности их распределения в сети, исходя из необходимой пропускной способности тракта передачи. Наиболее высокую приоритетность должны иметь требования, соответствующие использованию телевизионных каналов общенационального уровня, затем – телевизионных каналов регионального уровня, затем – мультимедийного трафика и т. д.

2) Построение очередного k-го плана При построении очередного плана производится последовательное распределение потоков требований на сети. Эта последовательность определяется в соответствии с проведенным ранжированием. Для каждого потока требований определяются пути множества допустимых путей распределения потока (ν = 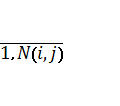), число которых ) либо заранее задается, либо определяется возможностями сети. Для формирования путей целесообразно использовать разработанные эффективные вычислительные алгоритмы решения задачи поиска заданного числа кратчайших путей, үоптимальных по заданному множеству частичных критериев [3]. Распределение частей потока требований по путям осуществляется пропорционально пропускным способностям 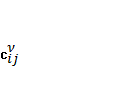этих путей. Для каждого пути плана – определение показателя качества обслуживания требований по данному пути (в соответствии(9)).

3) Формирование значения критерия оптимальности K() плана в соответствии (4).

4) Проверка условия получения решения задачи:

| K()- K()| ε, где ε – принятая точность решения.

здесь - номер очередного плана. В качестве исходного значения принимается K()=0. Если условие (10) выполняется, алгоритм работу заканчивает, иначе – переход к построению очередного плана – к.п. 2 алгоритма.

Необходимо отметить следующее. При построении начального () и каждого последующего плана загрузка () каждой ветви распределяемыми потоками определяется как суперпозиция величин потоков, использующих эту ветвь. В результатеможет оказаться, сто некоторые ветви «перегружены», .е. не выпоняется ограничение (6). Поэтому указанным ветвям назначается «штраф», величина которого определяется степенью их «перегрузки». «Штраф» может выражаться, например, в фиктивном уменьшении пропускной способности этих ветвей или показателей надежности и т.д., т.е. в ухудшении тех характеристик ветвей, которые являются определяющими при построении путей. Эта процедура обеспечивает уменьшение использования указанных ветвей при построении путей распределения потоков требований в очередном плане.

Сходимость алгоритма обеспечивает тем, что возможные величины перегрузок ветвей, т.е. невыполнение (6) в процессе построения планов следует контролировать таким образом, чтобы каждый последующий план отличался от предыдущего уменьшением значения максимальной величины перегрузок по всем ветвям сети. Полученный результирующий план (в соответствии с критерием (4)) содержит следующую информацию:

По каждому требованию :

- пути ϵ распределения частей потоков , при этом ;

- пропускные способности путей ϵ

По каждой ветви :

- величина суммароной пропускной способности ветви, используемой прираспеделении всех потоков требований;

- перечень потоков требований в пути распределения которых включена ветвь ;

- часть пропускной способности ветви , используемая в пути распределения потока требований ().

Крометого, для каждой ветви формируется информация о выполнении ограничения (6). Результирующий план должен быть построен таким образом, чтобы ограничения (5) и (6) выпонялись, однако, возможна ситуация, при которой ограничение (6) выполняется не для всех ветвей, используемых для распределения потоков в полученном плане. Его выполнение для некоторой ветви после окончания работы алгоритма свидетельствует о том, что заданная максимально возможная пропускная способность этой ветви не соответствует существующей потребности, т.е сеть не способна полностью обеспечить рапределение потоков требований. Следовательно, существует необходимость изменения заданной величины максимально возможной пропускной способности указанной ветви .

Таким образом, в результате работы алгоритма на основании полученного оптимального плана распределения потоков требований в сети в соответствии с критерием (4) гарантированного качества обслуживания потоков требований определяются необходимые пропускныеспособности тех ветвей сети, которые следует использовать при распределении потоков требований, т.е. определяется структура телекоммуникационной сети.

Литература:

1. Бусленко Н.П., Калашников В.В., Коваленко И.М. Лекции по теории сложных систем. – М.:Сов.Радио, 1973.-440с.

2. Основы моделирования сложных систем //Л.М.Дыхненко, В.Ф. Кабаненко, И.В. Кузьмин и др.: Под ред. И.В.Кузьмина. – Киев: Вища шк., 1981.-360с.

3. В.К. Борзенко, Л.М. Кемлнер. Многокритериальная оптимизация. Математические аспекты.-М.: Наука, 1989.-128с.