Д.т.н., проф. Лежнюк П.Д., к.т.н., доц. Рубаненко А.Е.,

асп. Килимчук А.В.

Винницкий национальный технический университет

Оптимальное Управление нормальными режимами ЭЛЕКТРОЭНЕРГЕТИЧЕСКОЙ СИСТЕМЫ с использованием кросс-трансформаторов.

Параллельная работа линий электропередач (ЛЭП) разного напряжения из-за высокой меры неоднородности вызывает трудности при транспортировании и распределении электроэнергии. Между электрическими сетями электроэнергетической системы (ЭЭС) из-за неоднородности возникают взаимные потоки мощности, которые загружают сети смежных энергоснабжающих компаний. Известно, что сети высокого напряжения разгружаются на параллельно работающие сети низкого напряжения. В результате этого возникают дополнительные потери электроэнергии, а также перегрузки коммутационных аппаратов и ЛЭП низкого напряжения.

Исследование меры влияния взаимных и транзитных перетоков мощности на уровень потерь электроэнергии является актуальной задачей. Ее решение позволит контролировать и оценивать влияние перетоков мощности магистральных электрических сетей на дополнительные потери в распределительных сетях областных энергетических компаний, а также анализировать последствия взаимовлияния электрических сетей. Компенсация дополнительных потерь электроэнергии в электрических сетях, вызванных их взаимовлиянием, возможна путем введения в контуры э.д.с. линейными регуляторами типа кросс-трансформаторов (КТ) и силовыми трансформаторами с РПН. То есть работа рассматриваемых здесь систем автоматического управления (САУ) трансформаторами связи ЭЭС, которые объединяют электрические сети разных напряжений в электрическую систему, направлена на уменьшение потерь электроэнергии при ее транспортировании в ЭЭС путем перераспределения естественных потоков мощности и принудительного приближения их к потокораспределению в однородной ЭЭС.

В работе задача оптимизации режимов ЭЭС ставится как задача автоматического управления, конечной целью решения которой является формирование закона оптимального управления режимами электрических сетей с учетом системного эффекта.

Закон оптимального управления нормальными режимами ЭЭС. Исследования показали, что использование обобщенных методов теории подобия дает возможность получить в критериальной форме аналитические зависимости между параметрами режимов [1]. В соответствии с поставленной задачей для формирования законов управления САУ необходимо получить критериальные зависимости между оптимальными управляющими воздействиями для решения задачи оптимизации токораспределения в ЭЭС в разных режимах ее работы. В качестве аргумента целевой функции целесообразно принять уравнительные э.д.с., которые вводятся в контуры ЭЭС с целью компенсации ее неоднородности.

Активные и реактивные составляющие уравнительных э.д.с. в критериальной форме (при условии, что базисный режим является оптимальным со значениями Е(б)ур.а∑, Е(б)ур.р∑, J(б)а∑, J(б)р∑, записанными в виде диагональных матриц) (1):

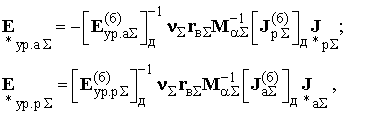                 (1)

где элементы векторов  определяются как отношение соответствующих параметров текущего и базисного режимов.

В такой постановке задачи, управляющими переменными являются э.д.с., которые необходимо ввести коэффициентами трансформации во все замкнутые контура для реализации оптимального токораспределения. В [2] показано, что оптимальное значение потерь в ЭЭС достигается при относительных значениях э.д.с., которые определяются в соответствии с формулами (2):

                          ,               (2)

где , – векторы активных и реактивных составляющих относительных значений уравнительных э.д.с. трансформаторов с РПН и кросс-трансформаторов, которыми вводятся уравнительные токи; ,  – векторы активных и реактивных составляющих относительных значений токов в узлах; ,  – матрицы критериев подобия.

Как видим, уравнительные э.д.с. оптимальных режимов определяются с учетом постоянных коэффициентов (критериев подобия), которые не зависят от параметров текущего режима. Они подобны соответствующим э.д.с. режима, принятого за базисный. То есть, в ЭЭС уравнительные э.д.с. подобны для разных режимов. Для определения оптимального режима ЭЭС остается ввести их в контура и выполнить расчет установившегося режима.

Матрицы критериев подобия определяются:

    ,   (3)

где  - матрица соединений веток в узлах дерева схемы.

Для автоматической реализации оптимальных коэффициентов трансформации необходимо получить соответствующие законы управления. Эта задача сводится к задаче формирования принятых в начале расчетных условий и может быть решена как описано в [3].

Из всех трансформаторов с РПН, в ЭЭС для управления потерями мощности отбираются (в результате критериального анализа) несколько (q) таких кросс-трансформаторов, которые имеют наибольший регулировочный эффект [1]. Если теперь расчетную модель ЭЭС сформировать таким образом, что все q трансформаторов будут находиться в хордах базисной системы контуров, то их коэффициенты трансформации будут равны:

.

Тогда вектор оптимальных коэффициентов трансформации запишется:

или

,

где k*а∑, k*р∑ – векторы действительных и мнимых составляющих коэффициентов трансформации в относительных единицах.

Последнее выражение коэффициентов трансформации для системы автоматического управления является законом оптимального управления нормальными режимами ЭЭС. С учетом фактора времени они записываются в таком виде (4):

              .                   (4)

Конечные расчетные формулы законов оптимального управления трансформаторами с РПН и с кросс-трансформаторами с учетом приведения параметров ЭЭС к напряжению базисного узла имеют вид 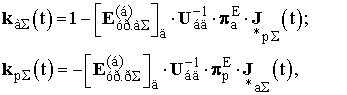(5):

                                                   (5)

где Uбд – диагональная матрица, каждый элемент которой равен напряжению базисного узла.

Данные законы являются основой функционирования CАУ [5]. Как видно из (5) они определяются неоднородностью и мерой несбалансированности коэффициентов трансформации трансформаторного оборудования ЭЭС. Их реализация компенсирует, с точностью до степени регулирования коэффициентов трансформации, неоптимальность потокораспределения в ЭЭС, которая вызвана неоднородностью и приближает потери мощности в ЭЭС к минимальным.

Как видно из (5), математическое описание законов функционирования САУ, регулируемыми трансформаторами, является достаточно сложным, а их формирование, адаптация и реализация, требуют существенных расходов машинного времени, особенно, учитывая необходимость коррекции матрицы критериев подобия в случае существенных изменений состояния регулировочных устройств. Необходимые вычисления потерь и объемы передачи информации могут быть существенно снижены, если на этапе математического моделирования учесть условия практической реализации разработанных моделей.

Математическая модель оптимального управления установившегося режима ЭЭС

Таким образом, получена математическая модель оптимального управления установившегося режима ЭЭС, во временной области, в виде линеаризованной многомерной системы с сосредоточенными постоянными параметрами.

Э.д.с. в контуры вводятся с совместной работой трансформаторов с РПН и КТ. С помощью КТ вводится базовая часть переменной во времени Е*ур э.д.с. Е*кт, к которой ступенями ΔE*АТ добавляется э.д.с. трансформаторов с РПН. С учетом связи между контурными э.д.с. и коэффициентами трансформации трансформаторов, при определенных условиях (трансформаторы в базовой системе контуров находятся в хордах, количество регулируемых трансформаторов равняется количеству контуров), коэффициенты трансформации КТ и трансформаторов с РПН могут быть переписаны в виде [6]:

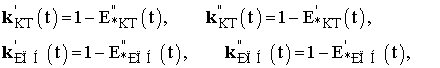
где  - векторы действительных и мнимых составляющих коэффициентов трансформации соответственно трансформаторов с РПН и КТ.

Выводы: разработана математическая модель уравнительных э.д.с. в электрических системах, которая в отличие от существующих, содержит коэффициенты трансформации кросс-трансформаторов и трансформаторов с РПН, что дает возможность учитывать влияние кросс-трансформаторов на уравнительные токи с целью уменьшения несбалансированных коэффициентов трансформации, неоднородности ЭЭС и последствия их взаимовлияния. Показано, что полученные критериальные зависимости являются законами оптимального управления. При определенных условиях они изменяются с учетом параметров кросс-трансформаторов и могут быть использованы в качестве законов управления адаптивных САУ нормальными режимами ЭЭС.

Литература

1. Лежнюк Петро Дем’янович, Автоматизація керування потоками потужності та напругою в електричних системах на основі теорії подібності /П.Д. Лежнюк, К.І. Кравцов, С.Я. Вишневський// Управління енерговикористанням: Збірник доповідей / Під ред. А.В. Праховніка. – К.: Альянс за збереження енергії, 2001. – С. 219–224.

2. Автоматизация управления энергообъединениями / Гончуков В.В., Горнштейн В.М., Крумм Л.А. и др. - М.: Энергия, 1979.- 432 с.

3. Petro Lezhnukm. Optimal control of power flows in electric power systems using theory of similarity /Petro Lezhnuk, Eugene Didichenko, Konstantin Kravtsov // Proceedings of the 5th International Conference on “Development and application systems” (DAS – 2000). – Suceava, Romania: “MUSATINII”, 2000. – С. 10–15.

4. Лежнюк Петро Де’мянович. Натурно-імітаційне моделювання з використанням критеріального методу в оптимальному керуванні електроненергетичними системами /П.Д. Лежнюк, В.М. Гайдамака // Вісник Вінницького політехнічного інституту. – 2003. – № 1. – С. 37-41.

5. Автоматизація керування потоками потужності в ЕЕС з використанням крос-трансформаторів та  подібності оптимальних режимів [Електронний ресурс] / П. Д. Лежнюк, Жан-П’єр Нгома, А. В. Килимчук // Вінницький національний технічний університет – 2009. – №4 – режим доступу до журн. http://www.nbuv.gov.ua/e-journals/vntu/2009-4/2009-4_ru.files/ru/09pdloms_ru.pdf