Волкова Н.І.
Дніпропетровський
національний університет
Абсолютна
сумовність ряду Фур’є з множником методом Вороного-Нерлунда
Послідовність ![]() , де
, де
![]()
де ![]() задана послідовність
дійсних або комплексних чисел, називається
задана послідовність
дійсних або комплексних чисел, називається ![]() – перетворенням ряду
– перетворенням ряду ![]() . Ряд
. Ряд ![]() називається абсолютно сумовним методом Вороного-Нерлунда, або
називається абсолютно сумовним методом Вороного-Нерлунда, або
![]() – сумовним на множині
– сумовним на множині ![]() , якщо
, якщо ![]()
![]()
![]() .
.
Нехай ![]() –
– ![]() -періодична
функція, інтегровна за Лебегом на
-періодична
функція, інтегровна за Лебегом на ![]() і
і ![]() – загальні члени ряду Фур’є і спряженого ряду Фур’є.
– загальні члени ряду Фур’є і спряженого ряду Фур’є.
Введемо позначення:
![]() ,
, ![]() ,
, ![]() ,
,
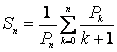 ,
, 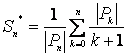
Якщо ![]() ,
, 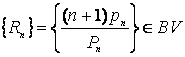 ,
,
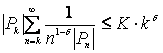 ,
, ![]() , то
, то ![]() .
.
Теорема 1. Якщо ![]() і
і ![]() ,
, ![]() ,
,
тоді ![]()
![]() – сумовний
– сумовний
Доведення. Для ряду Фур’є функції ![]()
![]() ,
, ![]() , тоді
, тоді
![]()
![]()
![]()
Оскільки ![]() , то для доведення теореми достатньо показати, що
, то для доведення теореми достатньо показати, що  .
.![]()
![]() .
.
Змінивши порядок сумування
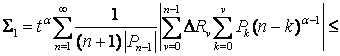
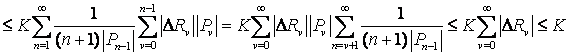
Оскільки ![]() для довільного
для довільного ![]() , то
, то
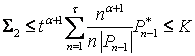 , оскільки
, оскільки ![]()
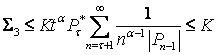 , оскільки
, оскільки ![]()
Оскільки ![]() , то приміняючи перетворення Абеля, одержимо
, то приміняючи перетворення Абеля, одержимо
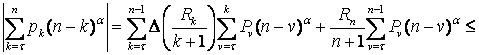
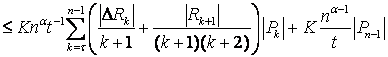
Розглянемо
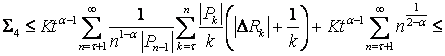
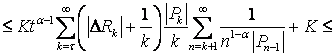
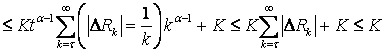
Об’єднуючи доведені нерівності стверджуємо, що ряд 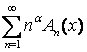 абсолютно сумовний методом Вороного-Нерлунда.
абсолютно сумовний методом Вороного-Нерлунда.
Теорема 2. Якщо ![]() і
і 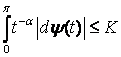 ,
, ![]() ,
, ![]() , тоді
, тоді 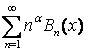
![]() - сумовний.
- сумовний.
Доведення. Інтегруючи частинами
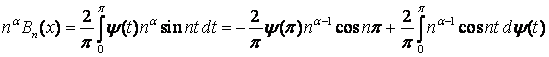
Розмірковуючи, як при доведенні теореми 1, маємо
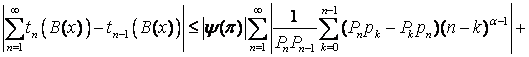
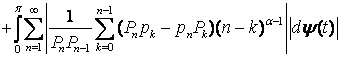
Оскільки 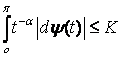 , то для доведення теореми достатньо показати, що
, то для доведення теореми достатньо показати, що 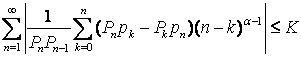 . Доводиться ця нерівність аналогічно, як доводиться
відповідна нерівність в теоремі 1.
. Доводиться ця нерівність аналогічно, як доводиться
відповідна нерівність в теоремі 1.