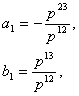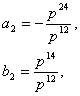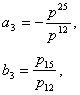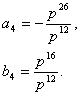Ищенко Е.Н.

Днепропетровский национальный университет

Многообразия пучков прямых в интерпретации Плюккера

 

Пусть  − трехмерное проективное пространство, а  − пятимерное проективное пространство с квадрикой Плюккера в нем. Плюккеровы координаты прямой в  обозначим символами . Для этих координат будем пользоваться ещё обозначениями

     

Эти координаты удовлетворяют фундаментальному условию Плюккера

                                                                                                   (1)

Уравнение (1) определяет квадрику Плюккера  Каждая прямая пространства  отображается в точку этой квадрики. Если имеем две пересекающиеся прямые в  с координатами  то для них будут выполняться условия

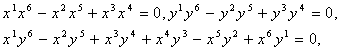                                                           (2)

В этом случае равенствами

 

определяется пучок прямых. В  этому пучку будет соответствовать прямая, принадлежащая квадрике Плюккера. Так как ставится задача исследовать свойства совокупности пучков прямых в  то эта задача приводит к задаче исследования линейчатых образов на квадрике Плюккера.

Найдём уравнения, определяющие прямые квадрики Плюккера. Сделаем это двумя способами.

1. Произвольную прямую пространства  можно задать с помощью четырёх линейных уравнений:

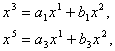
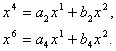                                                                           (3)

Эти уравнения показывают, что совокупность прямых в пространстве  является восьмипараметрической. Подставляя координаты  в уравнение (1) и приравнивая нулю коэффициенты  при    получим соотношения

                                                        (4)                                     

Эти равенства являются условиями того, что прямая (3) принадлежит квадрике Плюккра

Таким образом, совокупность всех прямых, принадлежащих квадрике , является пятипараметрической. Поэтому из этой совокупности можно образовать одно-, дву-, трёх- и четырёхпараметрические семейства прямых. Очевидно, в общем случае трёхпараметрическая совокупность прямых на   отображается на совокупность всех прямых пространства

2. Прямую пространства  можно задать с помощью плюккеровых координат. Для этого возьмем на ней две какие-нибудь точки. Не нарушая общности, можем считать, что такие точки заданы координатами

  и 

Будем обозначать плюккеровы координаты буквами  В таком случае будут иметь место следующие равенства:

                                        

                (5)

          

где  − множитель пропорциональности. Исключая из равенств (5) координаты   получим следующие квадратичные соотношения между плюккеровыми координатами прямой пространства :

            

                                                (6)

              

Не всякая прямая, плюккеровы которой удовлетворяют условиям (6), принадлежит квадрике . Для того, чтобы она принадлежала квадрике  необходимо и достаточно, чтобы выполнялись условия (2), которые в данном случае принимают вид

 

                     (7)

Подставив в равенства (7) значения коэффициентов из равенств (5), получим три дополнительные соотношения на плюккеровы координаты

                 (8)

Таким образом, пятнадцать плюккеровых координат  удовлетворяют девяти соотношениям (6) и (8). Учитывая однородность плюккеровых координат, остаётся  пять независимых координат. Это значит, что совокупность прямолинейных образующих квадрики Плюккера  является пятипараметрической.

Получены равенства, которые выражают связь между плюкеровыми координатами и координатами :

                                                          

                                                        

                                                                 (9)

                                                       

                                             

Из равенств (9) находим :

                                                              (10)

Исключение координат  из равенств (9) приводит к соотношениям (6). Подставив выражения (10) в соотношения (4), получим равенства (8).