Математика/1. Дифференциальные и

интегральные уравнения

 

Прохоренко М.В.

Національний універсистет водного господарства та

природокористування, Україна

 

До питання періодичності розв’язків диференціальних

рівнянь з імпульсною дією

 

       Розглянемо розривну динамічну систему [1], визначену в просторі Rn системою диференціальних рівнянь

                                                                                                                  (1)

( для всіх , квадратна матриця розміру  зі сталими коефіцієнтами, до того ж , спектр матриці ) та умовами імпульсної дії

                                                                                                                  (2)

(- задана гіперплощина,  - заданий вектор, константи).

       Рух фазової точки в системі (1)-(2) здійснюється по одній з траєкторій системи (1) в проміжку між двома послідовними попаданнями фазової точки на гіперплощину , а в момент попадання фазова точка  “миттєво” перекидається за законом (2) в точку гіперплощини , де , .

       Вважаємо, що:

                                                                                                                 (3)

                                     .                                            (4)

Співвідношення (3), (4) забезпечують розташування прямої  між  та початком координат.

В роботі [2] показано, що задача про існування періодичних розв’язків задачі (1)-(2) зводиться до задачі про існування нерухомих точок оператора

,

які шукаються з системи

                                                                                                                             (5)

де ; - період розв’язку.

       Для визначеності вважатимемо, що .

Теорема. Нехай  - діагональна матриця з дійсними елеменами . Для того, щоб при заданих  і  існував періодичний розв’язок системи (1)-(2) достатньо виконання однієї з умов:

1) ;

2) ,  при   і .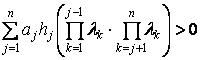

Доведення. З’ясуємо умови існування нерухомих точок оператора  для зазначених елементів матриці .

1) Нехай всі елементи матриці  дійсні, від’ємні і рівні між собою, тобто: . Тоді система (5) набуває вигляду

та має єдиний розв’язок

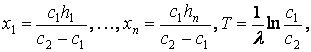
що при заданих  і  однозначно визначає координати нерухомої точки оператора Ф.

2) Нехай всі елементи матриці  дійсні, від’ємні та попарно різні. У цьому випадку система (5) запишеться у вигляді

розв’язком якої є координати нерухомої точки оператора Ф

,

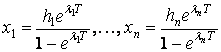а період  знаходиться з рівняння

                                                   .                              (6)

Знаходження розв’язку рівняння (6) еквівалентне відшуканню нулів функції

.

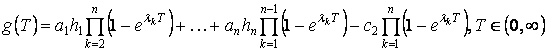Має місце гранична поведінка , ,  і  при 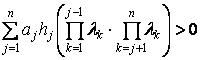. Тобто, за умови виконання теореми функція  матиме принаймі один нуль. Теорема доведена.

Література:

1.         Самойленко М.А., Перестюк Н.А. Дифференциальные уравнения с импульсным возействием.-К.: Наук.думка,1987. –216 с.

2.         Мороз М.В. Про існування періодичних розв’язків системи двох диференціальних рівнянь з імпульсною дією // Укр.мат.журн. -2002. – Т.54, №1.- С. 133-137.