Пыркова А.Ю.
Казахский Национальный Университет им. аль-Фараби,
г. Алматы, Казахстан
Математическое моделирование оптимального режима
введения лекарственного препарата
Существует
немало медико-биологических проблем /1,2/, к которым применимы известные математические
методы. Это прямая задача описания поведения физиологической системы во
времени; обратная задача определения степени достоверности различных гипотез на
основе сравнения теоретических и экспериментальных результатов, данные анализа
которых могут быть использованы для того, чтобы направлять дальнейший ход
эксперимента, и т. д.
Применение
математических методов к описанию физиологических процессов в общем случае
основывается на использовании математических моделей.
Проникновение
математических моделей с запаздыванием в медицину происходит не случайно.
Центральными становятся проблемы взаимодействия и развития /3,4/, что приводит
к необходимости привлечения для математического моделирования физиологических
систем организма дифференциально-разностных уравнений, учитывающих столь важный
для биологических систем эффект последействия. Использование импульсных
управляющих воздействий для таких моделей также не случайно, это связано с
практической пригодностью полученных результатов к медицинским моделям.
В данной работе рассматривается фармокинетическая двухкомпартментная (в некоторой литературе применяется термин двухкамерная) модель оптимального дозирования лекарственного препарата, представленная системой дифференциальных уравнений, управление которой происходит с помощью импульсных управляющих функций.
В
математических моделях, представляющих собой некоторые медицинские системы,
удобнее всего использовать импульсную функцию /5/. Удобнее, надо понимать в том
смысле, что в данной дифференциальной системе, представляющей собой некоторую
медицинскую модель, под управлением будет пониматься некоторое инъекционное
воздействие, которое, как очевидно, не происходит непрерывным образом.
Под
компартментом понимается некоторая физиологическая система организма, выполняющая
определенную функциональную нагрузку, в общем случае под компартментом можно
понимать весь организм. Двухкамерная модель организма представляет собой две
взаимосвязанных физиологических системы организма, функционирующие в
непосредственной зависимости друг от друга.
Пусть
в первый компартмент вводится лекарственный препарат, необходимый для
поддержания правильного функционирования системы. Следует заметить, что когда
концентрация вещества в компартменте I достигает своего заданного равновесного
уровня, концентрация вещества в компартменте II также достигает некоторого
уровня. В этом случае польза от наличия лекарственного препарата в компартменте
I, может быть меньше, чем вред нанесенный данным
лекарственным препаратом в компартменте II. Такими нежелательными эффектами
являются сыпь, головная боль, кожные повреждения.
Задача
состоит в том, чтобы сбалансировать терапевтическую пользу и потери от
интоксикации в некотором лучшем смысле.
Предположим, что поток жидкости в том или другом направлении
прямо пропорционален концентрации препарата в компартменте, создающем этот поток,
и что других взаимодействий между компартментами нет.
Тогда
двухкамерная модель достаточно просто описывается системой дифференциальных
уравнений второго порядка:
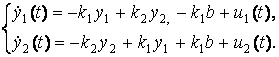
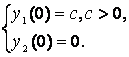 (1)
(1)
где ![]() - концентрация
препарата при
- концентрация
препарата при ![]() в компартменте I,
в компартменте I, ![]() - концентрация
препарата при
- концентрация
препарата при ![]() в компартменте II,
в компартменте II, ![]() - доза лекарственного
препарата, вводимого в момент времени
- доза лекарственного
препарата, вводимого в момент времени ![]() в компартмент I,
в компартмент I, ![]() - доза лекарственного
препарата, поступающая в момент времени
- доза лекарственного
препарата, поступающая в момент времени ![]() в компармент II.
в компармент II.
Необходимо
найти способы поддержания терапевтического уровня лекарственного препарата в
компартменте I, поддерживая в то же время концентрацию этого лекарственного
препарата в компартменте II на таком уровне, который не приводит к серьезным
побочным эффектам.
Предположим,
мы хотим приблизить ![]() , и в то же время хотим, чтобы
, и в то же время хотим, чтобы ![]() было мало, насколько
это возможно,
было мало, насколько
это возможно, ![]()
Будем
считать, что существуют величины ![]() , т. е. существуют способы измерений отклонений, соответствующих
пользе и вреду от применяемого препарата. Такие положительные функции
соответствующих концентраций будем рассматривать как «стоимость» терапии и
интоксикации.
, т. е. существуют способы измерений отклонений, соответствующих
пользе и вреду от применяемого препарата. Такие положительные функции
соответствующих концентраций будем рассматривать как «стоимость» терапии и
интоксикации.
Необходимо
выбрать режим введения лекарственного препарата таким образом, чтобы стоимости
терапии и интоксикации были минимальными, т.е. необходимо найти компромисс
между отклонением желаемого уровня в компартменте I и существованием некоторого
уровня в компартменте II, т.е. необходимо минимизировать следующий функционал
качества:
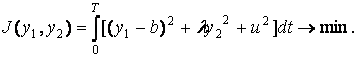 (2)
(2)
Сделаем
замену 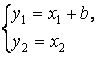 в системе (1) и
получим задачу оптимальной стабилизации на конечном отрезке времени с импульсным
управлением:
в системе (1) и
получим задачу оптимальной стабилизации на конечном отрезке времени с импульсным
управлением:
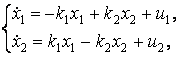 (3)
(3)
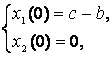 (4)
(4)
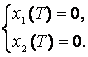 (5)
(5)
![]() (6)
(6)
Импульсная оптимальная стабилизация
на конечном отрезке времени. Пусть задана линейная управляемая
система /6,7,8/, описываемая системой дифференциальных уравнений вида
![]() (7)
(7)
где ![]() ,
, ![]() ,
, ![]() - векторы, причем
- векторы, причем ![]() - вектор фазового состояния системы имеет размерность
- вектор фазового состояния системы имеет размерность ![]() , вектор
, вектор ![]() - размерность
- размерность ![]() , а
, а ![]() - матрицы соответственно размерностей
- матрицы соответственно размерностей ![]() . Будем считать, что элементы матриц
. Будем считать, что элементы матриц ![]() и
и ![]() и
компоненты
и
компоненты ![]() мерной векторной функции
мерной векторной функции ![]() заданы при
заданы при ![]() , вещественны, непрерывны и ограничены.
, вещественны, непрерывны и ограничены.
Пусть требуется линейную управляемую систему (7) с помощью
управления типа обратной связи ![]() перевести из любого
фазового состояния
перевести из любого
фазового состояния ![]() при
при ![]() в конечное состояние
в конечное состояние ![]() при
при ![]() и при этом
минимизировать некоторый функционал качества /9/:
и при этом
минимизировать некоторый функционал качества /9/:
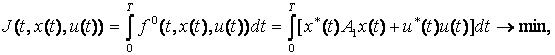 (8)
(8)
где ![]() - матрица с постоянными вещественными компонентами,
симметричная
- матрица с постоянными вещественными компонентами,
симметричная ![]() , размерности
, размерности ![]() ,
, ![]() - вещественная
кусочно-непрерывная функция.
- вещественная
кусочно-непрерывная функция.
На
вопрос, при каких условиях существует управление ![]() разрешающее выше
поставленную задачу, дает ответ следующая теорем.
разрешающее выше
поставленную задачу, дает ответ следующая теорем.
Теорема. Пусть
правая часть системы (7) удовлетворяет всем условиям теоремы о существовании
решения уравнения с разрывной правой частью
Каратеодори /10/.
Тогда
управление вида:
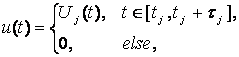 (9)
(9)
где
![]() (10)
(10)
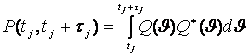 ,
(11)
,
(11)
![]() (12)
(12)
осуществляет
оптимальную стабилизацию движения системы (7) с квадратичным критерием качества
(8) на конечном отрезке времени.
Доказательство. Обозначим
через ![]() матрицу линейно независимых решений однородной системы
уравнений
матрицу линейно независимых решений однородной системы
уравнений ![]() , и будем считать, что
, и будем считать, что ![]() , где
, где ![]() - единичная матрица /11/.
- единичная матрица /11/.
Предположим,
что существует некоторое управление вида ![]() , которое осуществляет оптимальную стабилизацию системы (7),
(8) на конечном отрезке времени /12,13,14/.
, которое осуществляет оптимальную стабилизацию системы (7),
(8) на конечном отрезке времени /12,13,14/.
Воспользуемся
следующей методикой /15,16,17/. Умножим уравнение (7) справа на матрицу ![]() и проинтегрируем
полученное уравнение от
и проинтегрируем
полученное уравнение от ![]() до
до ![]() .
.
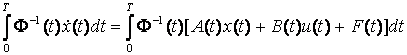 . (13)
. (13)
Проинтегрировав
интеграл, стоящий слева в равенстве (13) по частям и учитывая условие
стабилизации на конечном отрезке времени ![]() , получим:
, получим:
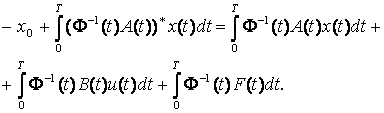 (14)
(14)
Согласно
(12), обозначим ![]() . Тогда получим следующее уравнение:
. Тогда получим следующее уравнение:
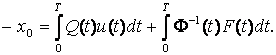 (15)
(15)
Будем
искать управление /12/ в виде (9), т. е.
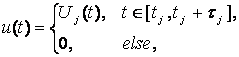 (16)
(16)
где
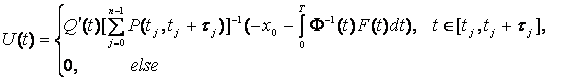
- некоторое
импульсное управление.
Подставим
управление (9) в уравнение (15), учитывая условия теоремы (10), (11) и (12).
Тогда получим:
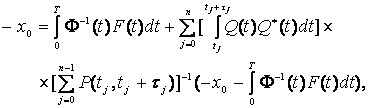 (17)
(17)
где 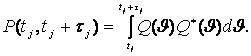 (18)
(18)
Теперь
остается показать, что управление вида (16) является оптимально стабилизирующим
управлением для системы (7) с квадратичным критерием качества (8).
Для
этого можно воспользоваться достаточными условиями Кротова В.Ф. /18/.
Согласно
теореме В.Ф. Кротова /18/, если допустимый процесс ![]() и некоторая функция
и некоторая функция ![]() удовлетворяют условию:
удовлетворяют условию:
![]() при всех
при всех ![]() ,
,
то тогда
процесс ![]() является оптимальным.
является оптимальным.
Функция
Кротова В.Ф. ![]() определяется следующим
образом:
определяется следующим
образом:
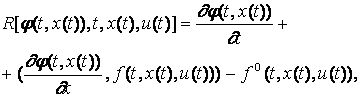 (19)
(19)
![]() .
(20)
.
(20)
![]() - правая часть системы
(7),
- правая часть системы
(7),
![]() - подынтегральное
выражение функционала (8).
- подынтегральное
выражение функционала (8).
В
качестве функции ![]() в функции Кротова /19/
для определения управления можно взять следующую функцию:
в функции Кротова /19/
для определения управления можно взять следующую функцию:
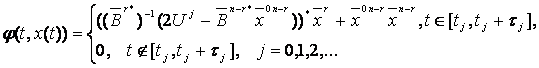 (21)
(21)
Теперь
нетрудно показать, что функция Кротова В.Ф. (19) при условии (21) достигает
своего максимального значения при управлении вида (16), т.е. выполнено
достаточное условие оптимальности Кротова В.Ф. /18/:
Это
означает, что управление:
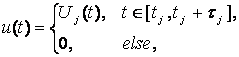 (22)
(22)
где
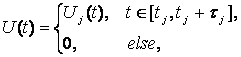 (23)
(23)
![]() (24)
(24)
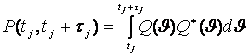 ,
(25)
,
(25)
![]() (26)
(26)
осуществляет
оптимальную стабилизацию системы (7) с квадратичным функционалом качества (8)
на конечном отрезке времени ![]() .
.
Теорема
доказана.
Алгоритм поиска оптимального
импульсного стабилизирующего управления. Согласно доказанной выше
теореме алгоритм синтеза оптимального импульсного стабилизирующего управления
можно представить следующим образом.
В
области ![]() пространства
пространства ![]() ,
, ![]() , где
, где ![]() ,
, ![]() ,
, ![]() будем рассматривать
систему дифференциальных уравнений:
будем рассматривать
систему дифференциальных уравнений:
![]()
где ![]() ,
, ![]() ,
, ![]() - векторы, причем
- векторы, причем ![]() - вектор фазового состояния системы имеет размерность
- вектор фазового состояния системы имеет размерность ![]() , вектор
, вектор ![]() - размерность
- размерность ![]() , а
, а ![]() - матрицы соответственно размерностей
- матрицы соответственно размерностей ![]() , с начальным условием:
, с начальным условием:
![]() ,
,
Задача
состоит в том, чтобы стабилизировать линейную управляемую систему на конечном
отрезке времени ![]() и при этом
минимизировать функционал качества:
и при этом
минимизировать функционал качества:

где ![]() - матрица с постоянными вещественными компонентами,
симметричная
- матрица с постоянными вещественными компонентами,
симметричная ![]() , размерности
, размерности ![]() ,
, ![]() - вещественная
кусочно-непрерывная функция.
- вещественная
кусочно-непрерывная функция.
Этап 1. Определяем стационарное
положение системы ![]() из равенства
из равенства ![]() .
.
Этап 2. Производим замену
переменных системы ![]() .
.
Этап 3. Подключаем управление. Система на данном этапе имеет вид:
![]() ,
, ![]()
с начальным условием:
![]() ,
,
а также добавляется условие стабилизации:
![]() .
.
Этап 4. Вычисляем матрицы ![]() ,
, ![]() .
.
Элементы матрицы ![]() определяем из системы
уравнений:
определяем из системы
уравнений:
![]() ,
,
![]() .
.
Матрица
![]() определяется из
соотношения:
определяется из
соотношения:
![]() .
.
Этап 6. Определяем оптимальное импульсное стабилизирующее управление, согласно формулам (9)-(12) для системы дифференциальных уравнений.
Этап 7. Решаем систему
![]() ,
, ![]()
с начальным условием:
![]()
и условием стабилизации:
![]()
некоторым численным методом, например методом Рунге-Кутта 4-го порядка.
Оптимальное дозирование
лекарственного препарата. Используя доказанную теорему можно определить режим
введения лекарственного препарата для двухкомпартментной модели (3)-(6) таким
образом, чтобы стоимости терапии и интоксикации были минимальными.
![]() (27)
(27)
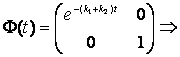
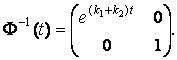 (28)
(28)
Обозначим
![]() .
.
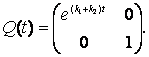 (29)
(29)
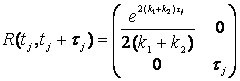 ,
(30)
,
(30)
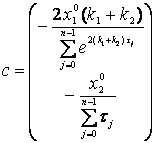 .
(31)
.
(31)
Таким
образом, ![]() (32)
(32)
где 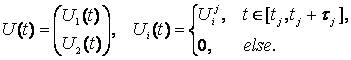 (33)
(33)
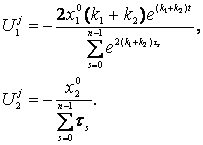 (34)
(34)
На
основе полученных результатов задача (3), (4), (5), (6) была решена
числено /20/ и графически (Рисунки 1, 2), в качестве начальных данных были
взяты экспериментальные значения /21/.
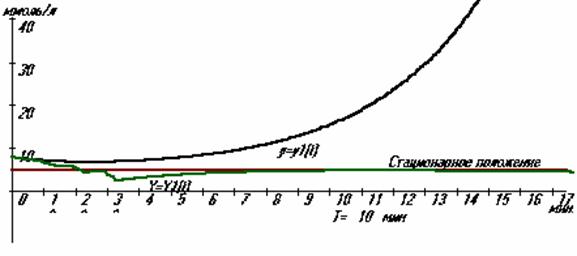
Рисунок 1. Изменение концентрации лекарственного препарата в
компартменте I.
![]() - нерегулируемое изменение концентрации,
- нерегулируемое изменение концентрации, ![]() - управляемый процесс,
значок ^ определяет момент импульса, длительность импульса
- управляемый процесс,
значок ^ определяет момент импульса, длительность импульса ![]() . Стационарное значение
. Стационарное значение ![]() , период
стабилизации
, период
стабилизации ![]() , параметры системы:
, параметры системы: ![]() ,
, ![]() , начальное
отклонение от стационарного значения
, начальное
отклонение от стационарного значения ![]() .
.
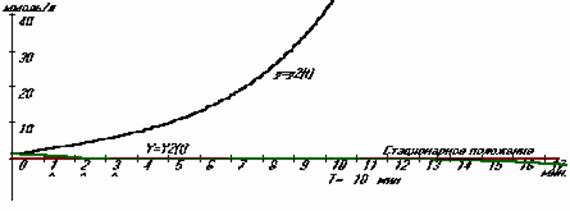
Рисунок 2. Изменение концентрации лекарственного препарата в
компартменте II.
![]() - нерегулируемое изменение концентрации,
- нерегулируемое изменение концентрации, ![]() - управляемый процесс,
значок ^ определяет момент импульса, длительность импульса
- управляемый процесс,
значок ^ определяет момент импульса, длительность импульса ![]() . Стационарное значение
. Стационарное значение ![]() , период
стабилизации
, период
стабилизации ![]() , параметры системы:
, параметры системы: ![]() ,
, ![]() , начальное
отклонение от стационарного значения
, начальное
отклонение от стационарного значения ![]() .
.
Список использованных источников
1.
Беллман Р. Кибернетика и медицинская диагностика. -
М.: Знание, 1968. - 48с.
2.
Марчук Г.И. Математические модели в иммунологии.
Вычислительные методы и эксперименты. - М.: Наука, 1991. - 304с.
3.
Николис Г., Пригожин И. Самоорганизация в
неравновесных системах. От диссипативных структур к упорядоченности через
флуктуации. - М.: Мир, 1976. - 512с.
4.
Николис Г., Пригожин И. Познание сложного:
Введение. - М.: Мир, 1990. - 342с.
5.
Бенсусан А., Лионс Ж.-А. Импульсное управление и
квазивариационные неравенства. - М.: Наука, 1987. - 600с.
6.
Пыркова А.Ю. Оптимальная стабилизация импульсных
систем. Математическая модель оптимального дозирования // Научный журнал
министерства образования и науки "Поиск". - 2000. - №1. - С. 161-168.
7.
Пыркова А.Ю. Оптимальная стабилизация импульсных
систем // Материалы XXXVIII
международной научной студенческой конференции "Студент и научно-технический
прогресс", Новосибирск, 2000, С. 42-43.
8.
Пыркова А.Ю. Оптимальная стабилизация импульсных
систем. Математическая модель оптимального дозирования // Материалы 54-ой
научной конференции студентов и молодых ученых "Молодежь - новому тысячелетию",
Алматы, 2000, С. 130-133.
9.
Михалевич Б.С., Попадинец В.И., Голодников А.Н.,
Ищенко А.В. Об одном классе задач оптимального управления процессами,
описываемыми обыкновенными дифференциальными уравнениями с дискретным множеством
управлений // Кибернетика. - 1983. - №4.
10.
Филиппов А.Ф. Дифференциальные уравнения с разрывной правой частью. - М.: Наука, 1985. - 224с.
11.
Арнольд В. Дополнительные главы теории обыкновенных
дифференциальных уравнений. - М.: Наука, 1978. - 304с.
12.
Бияров Т.Н. Устойчивость при постоянно действующих
возмущениях. Учебное пособие. - Алма-Ата: изд-во КазГУ, 1989.
13.
Алексеев В.М., Тихомиров В.М., Фомин С.В. Оптимальное
управление. - М.: Наука, 1979. - 432с.
14.
Фельдбаум А.А. Основы теории оптимальных
автоматических систем. - М.: Физматгиз, 1963. - 552с.
15.
Ройтенберг Я.Н. Автоматическое управление. - М.:
Наука, 1992. - 576с.
16.
Зубов В.И. Лекции по теории управления. - М.: Наука,
1975. - 495с.
17.
Прикладные задачи оптимального управления: модели,
методы, алгоритмы. Сборник трудов. - М.: Институт проблем управления, 1990. -
73с.
18.
Кротов В.Ф. Основы теории оптимального управления. -
М.: Высшая школа, 1990.
19.
Мурзабеков З.Н. Методические указания к лабораторным
работам по курсу "Оптимальное управление". - Алма-Ата: изд-во КазГУ,
1985.
20.
Хэмминг Р.В. Численные методы. - М.: , 1968.
21.
Беллман Р. Математические методы в медицине. - М.:
Мир, 1987. - 200с.