Мельник В.Н., Карачун В.В., Кладун Е.А.

Национальный технический университет Украины «КПИ»

ВЛИЯНИЕ ПРОНИКАЮЩЕГО АКУСТИЧЕСКОГО

ИЗЛУЧЕНИЯ НА ПОДВЕС ПОПЛАВКОВОГО ГИРОСКОПА

Наиболее опасным, с точки зрения влияния падающей звуковой волны, являются торцы поплавка гироскопа, имеющие существенно малую жесткость в направлении нормали [1, 2]. Поэтому представляет интерес описание природы явления и установление закономерностей возмущенного движения торцевой пластины подвижной части подвеса.

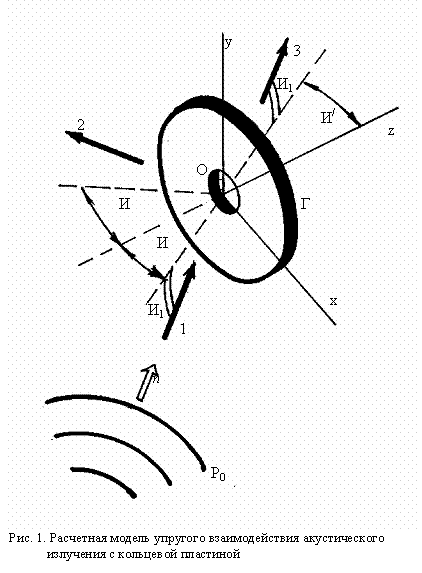
Расчетную модель построим в виде кольцевой пластины, как более общую (рис.1). При устремлении к нулю внутреннего радиуса , предельным переходом получаем сплошную круглую пластину.

Дифференциальное уравнение кольцевой пластины имеет вид [3] –

, (1)

где – бигармонический оператор; – цилиндрическая жесткость; – плотность внешней нагрузки (акустическое давление); ; – наружный радиус обоймы подшипника.

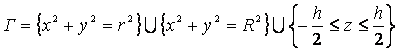– боковая поверхность пластины.

Граничными примем однородные условия

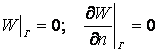, (2)

где – оператор дифференцирования по внешней нормали к боковой поверхности пластины .

В дальнейшем считаем, что правая часть исходного уравнения является средним значением функции на окружности , а угол изменяется в пределах , то есть –

. (3)

В этом случае можно утверждать , что изучаемая задача асимметрична, а потому решение уравнения (1) будет функцией только одной переменной, в данном случае – переменной :

.

Для удобства дальнейших вычислений перейдем к полярной системе координат. Тогда, с учетом осевой симметрии, имеем –

;

,

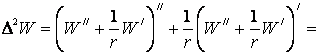
на основании чего можно утверждать о правомочности перехода к уравнению Эйлера

(4)

с однородными граничными условиями –

; ; ; . (5)

Пусть , где ; – безразмерная величина.

Тогда

; ;

; ;

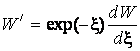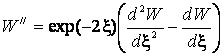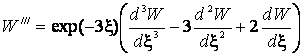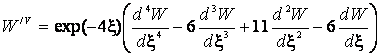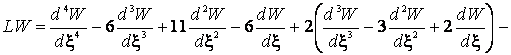
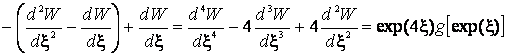. (6)

Пусть на пластину действует стационарная плоская звуковая волна вида

,

где – постоянные коэффициенты; – волновое число; – цилиндрическая жесткость пластины; – амплитуда звукового давления.

Обозначим : ; ; ; .

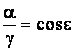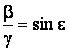Тогда –

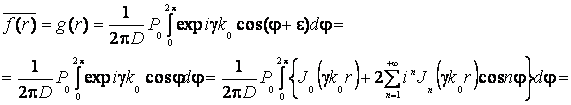
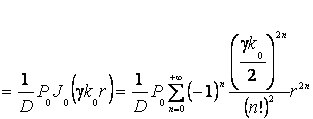(7)

и

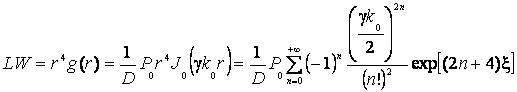, (8)

где .

Найдем частное решение уравнения (1.70) в виде суммы степенного ряда относительно

(9)

с коэффициентами , подлежащими определению.

Подстановка (9) в уравнение

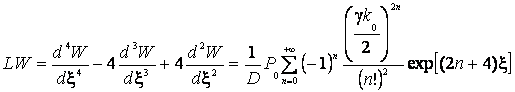(10)

дает:

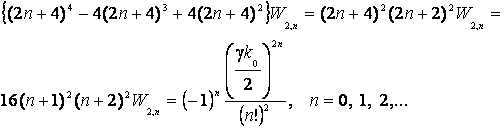
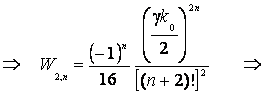
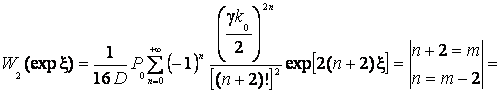
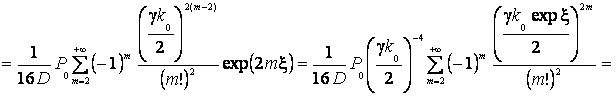
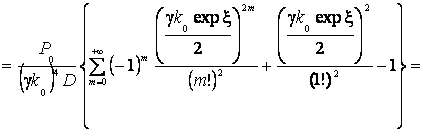
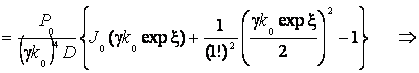
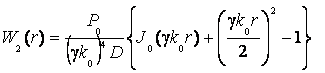(11)

Таким образом, решения уравнения (4) для этого случая имеет вид –

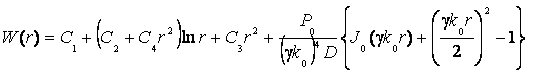. (12)

Разумеется, слагаемое 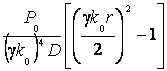можно было бы опустить, так как оно является частным решением однородного уравнения , и взять частное решение неоднородного уравнения (8) в такой форме –

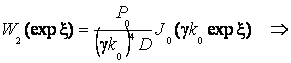
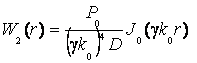. (13)

Таким образом, для плоской волны акустического воздействия предельное решение строится в виде:

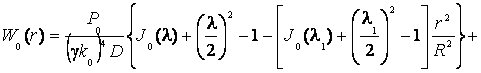
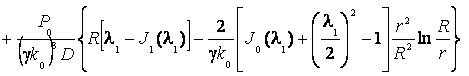, (14)

а значения определяются соотношением (11).

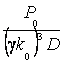Здесь – безразмерная переменная; – безразмерная константа; – безразмерная константа; .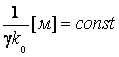

Литература:

1. Карачун В.В., Лозовик В.Г., Мельник В.Н. Дифракция звуковых волн на подвесе гироскопа. – К.: “Корнейчук”, 2000. – 176 с.

2. Mel’niсk V.N., Karachun V.V. Determining Gyroscopic Integrator Errors to Difraction of Sound Waves // INTERNATIONAL APPLIED MECHANICS. – 2004. – Vol. 40. - №3. – P. 328-336.

3. Василенко Н.В. Теория колебаний: Учебное пособие. – К.: Вища школа. 1992. – 430 с.