Пиль Э.А.

Академик РАЕ, д.т.н., профессор.

построение трехмерных графиков при расчете ввп

В представленной ниже статье рассматривается влияние пяти переменных на область существования ВВП, т.е. Vel (GDPel), т.е. Vel (GDPel) = f(Х1, Х2, Х3, Х4, Х5) и построения на их основе 3D графиков, которые являются более информативными, чем 2D графики, так как показывают влияние сразу двух переменных на рассчитываемую величину Vel (GDPel).

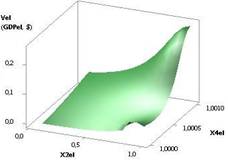
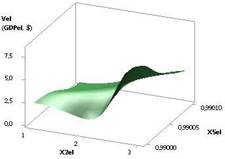
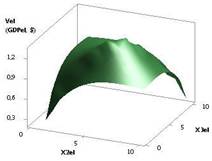
На рис. 1 показана зависимость Vel при Х1 = Х2 = Х3 = 1, Х4 = 1…0,1, Х5 = 0,99. Из данного рисунка видно, как 3D зависимость Vel (GDPel) изменяется от двух переменных Х1 и Х4.

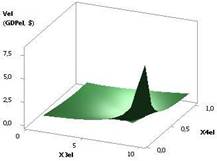
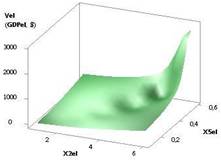
Рис. 1. Vel (GDPel) = f(Х1, Х2, Х3, Х4, Х5) Х1 = Х2 = Х3 = 1, Х4 = 1…0,1, Х5 = 0,99	Рис. 2. Vel (GDPel) = f(Х1, Х2, Х3, Х4, Х5) Х1 = Х4 = 1, Х2 = 1…0,1, Х3 = 1…10, Х5 = 0,99
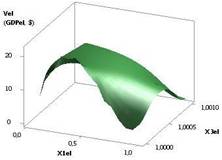
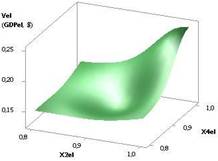
Рис. 3. Vel (GDPel) = f(Х1, Х2, Х3, Х4, Х5) Х1 = 1…0,1, Х2 = 1…10, Х3 = Х4 = 1, Х5 = 0,99	Рис. 4. Vel (GDPel) = f(Х1, Х2, Х3, Х4, Х5) Х1 = Х2 = 1, Х3 = 1…10, Х4 = 1…0,1, Х5 = 0,99

Следующий рис. 2 дает наглядное представление, где одна переменная Х3 увеличивается в 10 раз, а переменная Х4 уменьшается в 10 раз. При этом три переменные Х1, Х2 и Х5постоянные. Здесь значения Vel уменьшаются с 0,25 до 7,9Е-06.

На следующих двух рисунках 3 и 4 показаны две зависимости Vel (GDPel) = f(Х1, Х2, Х3, Х4, Х5), когда переменные были: Х1 = 1…0,1, Х2 = 1…10, Х3 = Х4 = 1, Х5 = 0,99 и Х1 = Х2 = 1, Х3 = 1…10, Х4 = 1…0,1, Х5 = 0,99 соответственно. Как видно из рис. 3 здесь, при данных значениях переменных, 3D зависимость Vel имеет максимум 21,75 в точке 7. Представленная 3D зависимость на рис. 4 имеет минимум 0,091 в точке 4 после чего растет до величины 7,93.

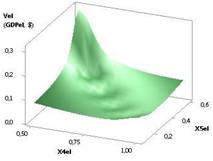
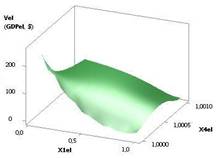
Рис. 5. Vel (GDPel) = f(Х1, Х2, Х3, Х4, Х5) Х1 = Х2 =1, Х3 =1…10, Х4 =1..0,1, Х5 =0,1…0,99		Рис. 6. Vel (GDPel) = f(Х1, Х2, Х3, Х4, Х5) Х1 = 1, Х2 = Х3 = 1…10, Х4 = 1…0,1, Х5 = 0,99
Рис. 7. Vel (GDPel) = f(Х1, Х2, Х3, Х4, Х5) Х1 = 1, Х2 = Х4 = 1…0,1, Х3 = 1…10, Х5 = 0,99	Рис. 8. Vel (GDPel) = f(Х1, Х2, Х3, Х4, Х5) Х1 = Х3 = 1…0,1, Х2 = 1…10, Х4 = 1, Х5 = 0,99

Следующие два рисунка 5 и 6 были построены при следующих значениях переменных Х1 = Х2 = 1, Х3 = 1…10, Х4 = 1..0,1, Х5 = 0,1…0,99 и Х1 = 1, Х2 = Х3 = 1…10, Х4 = 1…0,1, Х5 = 0,99. Здесь видно, что 3D зависимость имеет минимум 0,093 в точке 4 (рис. 5). Построенная же зависимость 3D на рис. 6 увеличивается незначительно с 0,25 до 8,17, т.е. 32,59 раза.

Две 3D зависимости, представленные на рис. 7 и 8 были построены при следующие значениях переменных Х1 = 1, Х2 = Х4 = 1…0,1, Х3 = 1…10, Х5 = 0,99 и Х1 = Х3 = 1…0,1, Х2 = 1…10, Х4 = 1, Х5 = 0,99. Здесь на рис. 7 построенная 3D зависимость имеют минимум 0,13 в точке 2. Трехмерная же зависимость Vel (GDPel) на рис. 8 увеличивается со значения 0,25 до250,62, т.е. в 1000,0 раза.

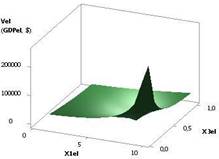
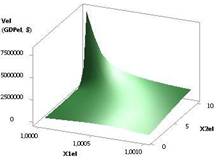
Зависимости, представленные Vel (GDPel) на рис. 9 и рис. 10, построены при следующих значениях: Х1 = Х2 = 1..10, Х3 = 1…0.1, Х4 = 1, Х5 = 0,99 и Х1 = 1…0.1, Х2 = Х3 = 1..10, Х4 = 1, Х5 = 0,99. Величина Vel на рис. 9 достигает значения 2,51Е+05 увеличившись в 1,0Е+06 раз, а для рис. 10 построенная область имеет максимум 1,3 в точках 5 и 6.

Рис. 9. Vel (GDPel) = f(Х1, Х2, Х3, Х4, Х5) Х1 = Х2 = 1..10, Х3 = 1..0.1, Х4 = 1, Х5 = 0,99	Рис. 10. Vel (GDPel) = f(Х1, Х2, Х3, Х4, Х5) Х1 = 1..0.1, Х2 = Х3 = 1..10, Х4 = 1, Х5 = 0,99
Рис. 11. Vel (GDPel) = f(Х1, Х2, Х3, Х4, Х5) Х1 = 1, Х2 = 1..10, Х3 = Х4 = 1..0.1, Х5 = 0,1..0,99	Рис. 12. Vel (GDPel) = f(Х1, Х2, Х3, Х4, Х5) Х1 = 1, Х2 = 1..10, Х3 = Х4 = 10.1,Х5 = 0,99…0,1

На последних двух рисунков 11 и 12 видно, что обе зависимости Vel (GDPel) увеличиваются. При этом их значения Vel (GDPel) увеличивались в 30383,73 и в 3,17Е+07 раза соответственно. Здесь следует отметить, что полученная расчетная величина Vel (GDPel) для рис. 12 является самой большой и достигает значения 7,93Е+06.

Эти рисунки были построены, когда значения переменных были следующими: Х1 = 1, Х2 = 1…10, Х3 = Х4 = 1…0.1, Х5 = 0,1…0,99 и Х1 = 1, Х2 = 1…10, Х3 = Х4 = 10.1,Х5 = 0,99…0,1.