Экономические науки/8. Математические методы в экономике
К.ф.-м.н. Зинченко А.Б., к.т.н. Мермельштейн Г.Г.,
Головкова Е.А.
Южный федеральный университет. Россия
Специальные классы сбалансированных
ТП игр
Кооперативная
игра с трансферабельной полезностью (ТП игра) определяется конечным множеством
участников (игроков, агентов) ![]() ,
, ![]() , и характеристической функцией
, и характеристической функцией ![]() ,
, ![]() . Значение
. Значение ![]() интерпретируется как максимальная полезность, которую могут
получить агенты коалиции
интерпретируется как максимальная полезность, которую могут
получить агенты коалиции ![]() , объединяя свои возможности (капиталы, ресурсы, акции).
Далее будем отождествлять игру
, объединяя свои возможности (капиталы, ресурсы, акции).
Далее будем отождествлять игру ![]() с ее
характеристической функцией
с ее
характеристической функцией ![]() .
.
Одним
из направлений развития кооперативной теории является изучение классов игр, имеющих
приложения, и исследование поведения их решений. Если игра, моделирующая
реальную ситуацию, принадлежит к изученному классу, то выбор решения и его вычисление
упрощаются. Упорядочим все непустые коалиции ![]() ,
, ![]() . Тогда игру n можно рассматривать как вектор пространства
. Тогда игру n можно рассматривать как вектор пространства ![]() , i-я
координата которого равна
, i-я
координата которого равна ![]() . Классы игр, образующих полиэдральные конусы в
. Классы игр, образующих полиэдральные конусы в ![]() , полностью определяются своими экстремальными элементами
(направляющими векторами ребер). Имея явное описание ребер конуса, можно
получить неограниченное количество практически неповторяющихся игр
рассматриваемого класса.
, полностью определяются своими экстремальными элементами
(направляющими векторами ребер). Имея явное описание ребер конуса, можно
получить неограниченное количество практически неповторяющихся игр
рассматриваемого класса.
Генерирование
экспериментальных данных для теории кооперативных игр актуально так же, как и
для других разделов теории принятия решений. Алгоритмы, имеющие плохие
теоретические оценки, могут отлично работать "в среднем" и наоборот.
Кроме вычислительного эксперимента, генераторы кооперативных игр нужны для
проверки гипотез, выявления свойств новых концепций решения, для тестирующих
программ, при создании учебных заданий. В отличие от многих других задач
исследования операций, все вычисления, связанные с кооперативной игрой, имеют
экспоненциальную сложность, т.к. уже "длина входа" равна ![]() , где
, где ![]() - количество игроков.
Ни одна из известных электронных библиотек тестовых примеров для методов теории
принятия решений (OR Library [1] и др.) не содержит раздел кооперативных игр.
- количество игроков.
Ни одна из известных электронных библиотек тестовых примеров для методов теории
принятия решений (OR Library [1] и др.) не содержит раздел кооперативных игр.
Основным
решением-множеством игры ![]() является С-ядро (core)
является С-ядро (core)
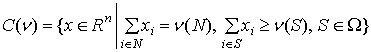 ,
,
где ![]() - множество
собственных коалиций. Игра, имеющая непустое С-ядро, называется сбалансированной.
Если функция
- множество
собственных коалиций. Игра, имеющая непустое С-ядро, называется сбалансированной.
Если функция ![]() задана таблично, то
проверка сбалансированности игры сводится к проверке совместности линейной
системы, определяющей С-ядро. Для кооперативных игр с характеристической
функцией, заданной аналитически, обычно используется критерий сбалансированности
Бондаревой-Шепли [2-3]
задана таблично, то
проверка сбалансированности игры сводится к проверке совместности линейной
системы, определяющей С-ядро. Для кооперативных игр с характеристической
функцией, заданной аналитически, обычно используется критерий сбалансированности
Бондаревой-Шепли [2-3]
эквивалентный условию
![]() ,
, ![]() ,
,
где ![]() - множество вершин
многогранника
- множество вершин
многогранника
![]() .
.
Семейство коалиций ![]() ,
где
,
где ![]() ,
, ![]() , называется минимальным сбалансированным
множеством (м.с.м.), если существует такая вершина
, называется минимальным сбалансированным
множеством (м.с.м.), если существует такая вершина ![]() , что
, что ![]() для
для ![]() и
и ![]() для
для ![]() . Вектор
. Вектор ![]() положительных компонент
вершины
положительных компонент
вершины ![]() назовем весом м.с.м.
назовем весом м.с.м. ![]() .
Пусть
.
Пусть ![]() - семейство
всех м.с.м., тогда критерий сбалансированности игры
- семейство
всех м.с.м., тогда критерий сбалансированности игры ![]() можно записать в виде
можно записать в виде
![]() ,
, ![]() . (1)
. (1)
Количество неравенств системы (1) резко возрастает при
увеличении числа игроков.
В данной статье рассматриваются подмножества (0,1)-нормализованных
ТП игр,
удовлетворяющих более простым, чем (1), но только достаточным условиям
сбалансированности. Исследуются
соотношения между этими подмножествами, приводится содержательная интерпретация определяющих их
неравенств. Получены формулы, определяющие некоторые классы экстремальных игр.
Напомним, что
агент ![]() является
вето-игроком, если
является
вето-игроком, если ![]() ,
, ![]() . Игра
. Игра ![]() называется:
называется:
·
неотрицательной, если ![]() ,
, ![]() ;
;
·
(0,1)-нормализованной, если
![]() ,
, ![]() ,
, ![]() ; (2)
; (2)
·
супераддитивной, если ![]() ,
, ![]() =Æ,
=Æ, ![]() ;
;
·
выпуклой, если ![]() ,
, ![]() ;
;
·
вогнутой, если ![]() ,
, ![]() ;
;
·
1-выпуклой [4], если
![]() , (3)
, (3)
![]() ,
,![]() ; (4)
; (4)
·
простой, если ![]() и
и ![]() ;
;
·
простейшей (игрой единогласия ![]() коалиции
коалиции ![]() ,
, ![]() ), если
), если ![]() для
для ![]() и
и ![]() в остальных случаях.
в остальных случаях.
Без
ограничения общности будем рассматривать неотрицательные игры. Если ![]() для некоторой
коалиции
для некоторой
коалиции ![]() , то, прибавляя к
, то, прибавляя к ![]() такую функцию
такую функцию ![]() , что
, что ![]() ,
, ![]() ,
, ![]() и
и ![]() , получаем игру
, получаем игру ![]() , в которой
, в которой ![]() . Если
. Если ![]() для нескольких
коалиций, то процедура повторяется. Такое преобразование не влияет на свойства
основных решений игры
для нескольких
коалиций, то процедура повторяется. Такое преобразование не влияет на свойства
основных решений игры ![]() . Для простоты, ограничимся исследованием
(0,1)-нормализованных игр. При (0,1)-нормализации конусы специальных классов
игр отображаются в многогранники, а ребра конусов – в вершины многогранников.
. Для простоты, ограничимся исследованием
(0,1)-нормализованных игр. При (0,1)-нормализации конусы специальных классов
игр отображаются в многогранники, а ребра конусов – в вершины многогранников.
Многогранники неотрицательных
супераддитивных (superadditive), выпуклых (convex), вогнутых (concave),
1-выпуклых (1-convex) и сбалансированных (balanced) игр ![]() лиц в (0,1)-форме будем
соответственно обозначать
лиц в (0,1)-форме будем
соответственно обозначать ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Справедливы следующие соотношения:
. Справедливы следующие соотношения:
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Примечательно, что
несупераддитивная и немонотонная игра может быть сбалансированной.
В некоторых социально-экономических ситуациях,
моделируемых кооперативными играми, один из участников имеет большие
возможности (большую силу), чем остальные: рынок с одним продавцом и
несколькими покупателям, парламент с одной большой и несколькими малыми
партиями, аналогичные ситуации банкротства и инвестирования, аукционы, холдинг.
Игрок, имеющий большую силу, называется боссом. Остальные игроки
называются малыми (слабыми). Коалиция, не содержащая босса, называется союзом.
Монотонная игра
большого босса [5] с игроком 1 в
качестве босса определяется условиями:
![]() ,
, ![]() (монотонность);
(монотонность);
![]() ,
, ![]() (свойство босса);
(свойство босса);
![]() ,
, ![]() ,
, ![]() (свойство союза),
(свойство союза),
где ![]() ,
, ![]() , - вклады игроков в максимальную коалицию
, - вклады игроков в максимальную коалицию ![]() (маргинальные
вклады).
(маргинальные
вклады).
Если
условие монотонности заменить условием неотрицательности игры и маргинальных
вкладов, то получим немонотонную игру большого босса, являющуюся частным
случаем клановой игры [6]. Клановая игра с коалицией ![]() в качестве клана
моделирует ситуацию с группой
в качестве клана
моделирует ситуацию с группой ![]() сильных агентов и
определяется условиями:
сильных агентов и
определяется условиями:
![]() ,
, ![]() ,
, ![]() ,
, ![]() (неотрицательность);
(неотрицательность);
![]() ,
, ![]() (свойство клана);
(свойство клана);
![]() ,
, ![]() (свойство союза).
(свойство союза).
Многогранники
(0,1)-нормализованных монотонных и немонотонных игр большого босса (big boss games) с игроком ![]() в качестве босса, а
также клановых игр (clan games) с коалицией
в качестве босса, а
также клановых игр (clan games) с коалицией ![]() в качестве клана
будем соответственно обозначать
в качестве клана
будем соответственно обозначать ![]() ,
, ![]() ,
, ![]() . Из включений
. Из включений
![]() ,
, ![]() ,
,
![]() ,
, ![]()
следует, что условия, определяющие
выпуклые игры, 1-выпуклые игры, игры большого босса и клановые, являются
достаточными для сбалансированности игры ![]() .
.
Неравенства
из условий супераддитивности, выпуклости, вогнутости и 1-выпуклости имеют
следующую содержательную интерпретацию. Супераддитивность означает, что любые
две непересекающиеся коалиции после объединения могут обеспечить себе не меньшую
полезность, чем, действуя самостоятельно. В выпуклой (вогнутой) игре вклад ![]() игрока
игрока ![]() в коалицию
в коалицию ![]() не убывает (не
возрастает) при увеличении мощности коалиции. Участники выпуклой игры стремятся
к всеобщему объединению. Неравенство (3) из условия 1-выпуклости содержится в
условии сбалансированности (1). Оно соответствует м.с.м.
не убывает (не
возрастает) при увеличении мощности коалиции. Участники выпуклой игры стремятся
к всеобщему объединению. Неравенство (3) из условия 1-выпуклости содержится в
условии сбалансированности (1). Оно соответствует м.с.м. ![]() с весом
с весом ![]() и обеспечивает
непустоту множества двойственных дележей
и обеспечивает
непустоту множества двойственных дележей
![]() .
.
Запишем (3) в виде ![]() . Теперь видно, что полезность
. Теперь видно, что полезность ![]() , достижимая для максимальной коалиции, не должна быть больше
суммы
, достижимая для максимальной коалиции, не должна быть больше
суммы ![]() маргинальных вкладов
всех игроков. Вторая часть условия 1-выпуклости эквивалентная
маргинальных вкладов
всех игроков. Вторая часть условия 1-выпуклости эквивалентная
![]() ,
, ![]() ,
,
требует, чтобы сумма маргинальных вкладов ![]() игроков каждой коалиции
игроков каждой коалиции![]() (
(![]() ) была не больше вклада
) была не больше вклада ![]() этой коалиции в
максимальную коалицию
этой коалиции в
максимальную коалицию ![]() . Очевидно, это условие содержит условия союза из определений
игры большого босса и клановой игры, означающие, что слабые игроки успешней
действуют при объединении. В классе (0,1)-нормализованных игр
. Очевидно, это условие содержит условия союза из определений
игры большого босса и клановой игры, означающие, что слабые игроки успешней
действуют при объединении. В классе (0,1)-нормализованных игр ![]() . Тем не менее, неравенства из условия (4) для
. Тем не менее, неравенства из условия (4) для ![]() -элементных коалиций
-элементных коалиций ![]()
![]() ,
,
содержатся в
условии вогнутости. Следовательно, в 1-выпуклых играх, играх большого босса и
клановых играх образование некоторых коалиций невыгодно.
Количество неравенств в условии
сбалансированности (1) известно только для малых ![]() . Для неотрицательных (0,1)-нормализованных игр тест на
выпуклость (1-выпуклость) состоит из
. Для неотрицательных (0,1)-нормализованных игр тест на
выпуклость (1-выпуклость) состоит из 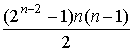 (
(![]() ) неравенств (см. таблицу 1). Неприводимая система,
определяющая игру
) неравенств (см. таблицу 1). Неприводимая система,
определяющая игру ![]() , получена в [7], но формула для количества неравенств
в системе не выведена.
, получена в [7], но формула для количества неравенств
в системе не выведена.
Таблица 1
Количество неравенств в системах, определяющих
многогранники
![]() ,
, ![]() ,
, ![]()
|
|
Количество неравенств |
|||
|
Число игроков |
3 |
4 |
5 |
6 |
|
Сбалансированная
игра |
5 |
41 |
1291 |
200213 |
|
Выпуклая
игра |
3 |
18 |
70 |
225 |
|
1-выпуклая
игра |
4 |
11 |
26 |
57 |
Проблема
характеризации экстремальных игр многогранников немонотонных игр большого босса
и клановых игр решена. Из результатов работы [6] следует, что вершинами этих
многогранников являются простые игры, т.е. многогранники целочисленны. Количество
вершин в ![]() равно
равно
![]() ,
,
где ![]() . Положив
. Положив ![]() , получаем оценку количества вершин многогранника
, получаем оценку количества вершин многогранника ![]() .
.
Нетрудно
доказать, что многогранники выпуклых, 1-выпуклых игр и немонотонных игр
большого босса содержатся в ![]() -мерном единичном гиперкубе, поэтому компоненты их
целочисленных вершин могут принимать только значения 0 или 1. В
(0,1)-нормализованной игре
-мерном единичном гиперкубе, поэтому компоненты их
целочисленных вершин могут принимать только значения 0 или 1. В
(0,1)-нормализованной игре ![]() , значит целочисленными вершинами многогранников
, значит целочисленными вершинами многогранников ![]() ,
, ![]() и
и ![]() (аналогично
(аналогично ![]() ,
, ![]() ,
, ![]() ) могут быть только простые игры. Многогранники
) могут быть только простые игры. Многогранники ![]() и
и ![]() целочисленные
[7], но при
целочисленные
[7], но при ![]() у них появляются
нецелочисленные вершины. Некоторые классы вершин общего многогранника
у них появляются
нецелочисленные вершины. Некоторые классы вершин общего многогранника ![]() описаны [7].
описаны [7].
Экстремальные векторы конуса выпуклых игр
4-х лиц опубликованы в статье Л.Шепли ([8], с.14). Им соответствуют 36 вершин
многогранника ![]() , составляющих 10 классов эквивалентности. Игры каждого
класса отличаются нумерацией игроков. Анализ экстремальных игр показывает, что:
, составляющих 10 классов эквивалентности. Игры каждого
класса отличаются нумерацией игроков. Анализ экстремальных игр показывает, что:
-
все целочисленные
вершины являются играми единогласия коалиций, содержащих не менее двух игроков;
-
игры единогласия ![]() 2-х элементных
коалиций
2-х элементных
коалиций ![]() , являются играми большого босса (боссом можно считать
любого агента коалиции
, являются играми большого босса (боссом можно считать
любого агента коалиции ![]() );
);
-
все остальные
экстремальные игры не содержат босса;
-
три
одноэлементных класса состоят из симметричных игр.
В работе [8] сказано, что об экстремальных элементах
конуса выпуклых игр пяти и более лиц ничего не известно. Из утверждения о
неотрицательности коэффициентов разложения ![]() выпуклой игры по
стандартному базису, состоящему из игр единогласия
выпуклой игры по
стандартному базису, состоящему из игр единогласия ![]() [9], и предположения
о (0,1)-нормализованности игры, вытекает, что целочисленными вершинами многогранника
[9], и предположения
о (0,1)-нормализованности игры, вытекает, что целочисленными вершинами многогранника
![]() являются игры
единогласия
являются игры
единогласия ![]() ,
, ![]() , и только они. Количество
таких игр равно
, и только они. Количество
таких игр равно ![]() . Нетрудно также описать все симметричные экстремальные
выпуклые игры. В симметричной игре значение
. Нетрудно также описать все симметричные экстремальные
выпуклые игры. В симметричной игре значение ![]() зависит только от мощности
коалиции
зависит только от мощности
коалиции ![]() , поэтому
, поэтому ![]() обозначим через
обозначим через ![]() . Минимальный тест на выпуклость [9]
. Минимальный тест на выпуклость [9]
преобразуется в систему ![]() неравенств
неравенств
![]() ,
, ![]() .
.
Множество ![]() содержит
содержит ![]() симметричных игр
симметричных игр ![]() (см. таблицу 2), где
(см. таблицу 2), где ![]() ,
,
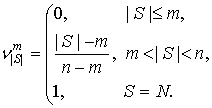
Таблица 2
Симметричные экстремальные игры многогранников ![]() -
-![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Заметим, что С-ядра игр из ![]() , определенных векторами
, определенных векторами
![]() ,
, ![]() ,
,
совпадают с множеством дележей и двойственных дележей
соответственно. В [10] доказано, что симметричная игра
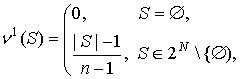
является единственной игрой, одновременно выпуклой и
1-выпуклой.
Насколько известно авторам, структура
многогранника ![]() не
исследовалась. Численный эксперимент, проведенный для многогранника
не
исследовалась. Численный эксперимент, проведенный для многогранника ![]() с помощью
программы [11], показал, что
с помощью
программы [11], показал, что ![]() . В
. В ![]() больше вершин,
чем в
больше вершин,
чем в ![]() , но экстремальные игры имеют С-ядра только двух типов.
С-ядро игр из
, но экстремальные игры имеют С-ядра только двух типов.
С-ядро игр из ![]() состоят из
единственного элемента, совпадающего с переговорным множеством (bargaining set)
[12], К-ядром (kernel) [13], лексикографическим
ядром (lexicore) [14], N-ядром (nucleolus) [15], t-значением (
состоят из
единственного элемента, совпадающего с переговорным множеством (bargaining set)
[12], К-ядром (kernel) [13], лексикографическим
ядром (lexicore) [14], N-ядром (nucleolus) [15], t-значением (![]() -value) [4] и AL-значением (AL-value) [14], т.е. сочетает много принципов
"справедливого" распределения веса
-value) [4] и AL-значением (AL-value) [14], т.е. сочетает много принципов
"справедливого" распределения веса ![]() максимальной
коалиции. В теории кооперативных игр одноэлементное С-ядро считается идеальным
решением. Тем не менее, для игр из
максимальной
коалиции. В теории кооперативных игр одноэлементное С-ядро считается идеальным
решением. Тем не менее, для игр из ![]() концепция
С-ядра не подходит, т.к. единственный дележ С-ядра отдает всю кооперативную
прибыль боссу, несмотря на его нулевые собственные возможности. В играх
большого босса с одноэлементным С-ядром лучше использовать значение Шепли.
концепция
С-ядра не подходит, т.к. единственный дележ С-ядра отдает всю кооперативную
прибыль боссу, несмотря на его нулевые собственные возможности. В играх
большого босса с одноэлементным С-ядром лучше использовать значение Шепли.
Литература:
1. Beasley J.E.
OR-Library: distributing test problems by electronic mail // Journal of the
Operational Research Society. 1990. V. 41.
P.
1069-107.
2. Shapley L.S. On
balanced sets and cores // Naval Research Logistics Quarterly. 1967. V. 14. P.
453-460.
3.
Бондарева О.Н. Некоторые применения методов линейного
программирования к теории кооперативных игр // Проблемы кибернетики. 1963. Вып.
10. С. 119-140.
4. Driessen T.S.H.,
Tijs S.H. The t -value, the
nucleolus and the core for a subclass of games // Methods Operations Research.
1983. V. 46. P. 395–406.
5.
Muto S., Nakayama M., Potters J., Tijs S. On big boss games // The
Economic Studies Quarterly. 1988. V. 39. P. 303-321.
6.
Potters J., Poos R., Muto S., Tijs S. Clan games // Games and Economic
Behavior. 1989. № 1. P. 275–293.
7. Зинченко А.Б. Свойства многогранника специальных
функций множества // Известия
вузов. Сев.-Кавказ. регион. Естественные науки. 2012.
№ 1. С. 13-17.
8. Shapley L.S. Cores
of convex games // International Journal of Game Theory. 1971. № 1. P. 11-26.
9. Voorneveld M.,
Grahn S. A minimal test for convex games and the Shapley value // Working paper
series, Department of economics, Uppsala university. 2001. № 2. P. 1-8.
10.
Зинченко А.Б.
Устойчивость ядер кооперативной игры в форме характеристической функции //
Известия вузов. Сев.-Кавказ. регион. Естественные науки. 2014. № 3. С. 14-18.
11.
Cdd Home Page: http://www.ifor.math.ethz.ch/~fukuda/cdd_home/cdd.html.
12. Aumann R.J.,
Maschler M. The bargaining set for cooperative games // Advances in Game
Theory. Princeton University Press. Princeton. 1964. P. 443-447.
13. Davis M., Maschler
M. The kernel of a cooperative game // Naval Research Logistics Quarterly.
1965. V. 12. P. 223-259.
14. Tijs S. The first
steps with ALEXIA, the average lexicographic value // CentER DP 2005-123.
Tilburg University. Tilburg. The Netherlands. 2005.
15. Schmeidler D. The
nucleolus of a characteristic function game // SIAM Journal of Applied
Mathematics. 1969. V. 17, P. 1163-1170.