Асанова А.Т., Сабалахова А.П.,
Байгулова Н.З.
Южно-Казахстанский
государственный университет им. М.Ауезова, Казахстан
Об однозначной
разрешимости нелокальной краевой задаче для дифференциального уравнения
четвертого порядка
В прямоугольнике 
для
дифференциального уравнения в частных производных четвертого порядка 
, (1)
рассматривается
нелокальная краевая задача
, 
, (2)
, 
, (3)
, 
, (4)
, 
,
(5)
где функции 
, 
непрерывны на 
, 
, 
, функции 
, 
дважды непрерывно
дифференцируемы на 
, 
, соответственно, функция 
непрерывно
дифференцируема на 
, функции 
, 
, 
непрерывны на 
, и выполняются
условия согласования:
, 
, 
.
Дифференциальные уравнения
в частных производных четвертого порядка
и краевые задачи для них часто возникают при исследовании процессов динамики упругопластических
микроструктур, в квантовой физике, в теории расширяемых балок и др. [1-4].
Возрастающий интерес к нелокальным задачам для дифференциальных уравнений в частных производных четвертого
порядка связан как с их большим прикладным
значением, так и в неклассическом характере изучаемого уравнения.
Решением нелокальной краевой задачи для
дифференциального уравнения в частных производных четвертого порядка (1)-(5)
называется функция 
, непрерывная на 
, имеющая непрерывные частные производные 
, 
, 
, 
, 
, 
, 
, 
на 
, удовлетворяющая
уравнению (1) и краевым условиям
(2)-(5).
В настоящей работе
исследуются вопросы существования, единственности решения нелокальной краевой
задачи для дифференциального уравнения в частных производных четвертого
порядка (1)-(5), а также приближенные
методы нахождения ее решений. В этих
целях к задаче применяется метод введения функциональных параметров [5-14],
разработанный в работах одного из авторов для решения нелокальных краевых
задач для системы гиперболических
уравнений со смешанными производными. Исследуемая задача с помощью новых
неизвестных функций сведена к нелокальной краевой задаче для системы
гиперболических уравнений второго порядка и функциональным соотношениям.
Предложен способ нахождения решения рассматриваемой задачи. Получены условия
существования единственного решения нелокальной краевой задачи для
дифференциального уравнения в частных производных четвертого порядка (1)-(5)
в терминах коэффициентов уравнения и граничных функций.
Введем новые неизвестные функции
, 
, 
и от задачи (1)-(5) перейдем к эквивалентной задаче
, (6)
, 
, (7)
, 
, (8)
, 
, 
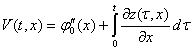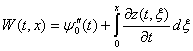. (9)
где 
, 
, 
, 
, 
, 
, 
, 
, 
, 
.
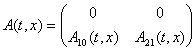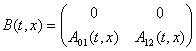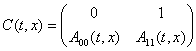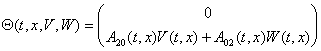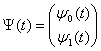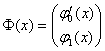Решением задачи (6)-(9)
является четверка функций 
, где непрерывные на 
функции 
, 
, 
, 
удовлетворяют
системе уравнений (6), краевым условиям (7)-(8), а функции 
, 
связаны
соотношениями (9) с функцией 
.
При фиксированных 
, 
, задача (6)-(9) является нелокальной краевой задачей для системы гиперболических
уравнений второго порядка относительно
функции 
, координаты которого составляют функции 
, 
.
Нелокальная краевая
задача (6)-(9) была всесторонне изучена
в работах [5,7,8]. Построены алгоритмы нахождения решения и
получены условия однозначной классической разрешимости рассматриваемой задачи. Также были установлены необходимые и
достаточные условия корректной
разрешимости нелокальной краевой задачи
для системы гиперболических уравнений второго порядка в терминах исходных данных [6,9,10].
Если известны функции 
, 
, из нелокальной краевой задачи (6)-(8) можно найти функции 
, 
, а если известна функция 
, из функциональных соотношений (9) через ее производные по 
, 
можно найти функции 
, 
.
Так как неизвестными являются и функции 
, 
, и функции 
, 
, применяется
итерационный процесс, а
последовательные приближения - четверка
функций 
определяются по следующему алгоритму:
0-шаг.
1) Считая 
, 
, из
нелокальной краевой задачи
для системы гиперболических уравнений второго порядка (6)-(8) находим 
, 
; 2) Из функциональных соотношений (9) при 
, 
, находим 
, 
, 
.
1-шаг. 1) Считая 
, 
, из нелокальной
краевой задачи для системы гиперболических уравнений (6)-(8) находим 
, 
; 2) Из функциональных соотношений (9) при 
, 
, находим 
, 
, 
.
И т.д.
-шаг. 1) Считая 
, 
, из нелокальной
краевой задачи для системы гиперболических уравнений (6)-(8) находим 
, 
; 2) Из функциональных соотношений (11) при 
, 
, находим 
, 
, 
, 
.
Условия осуществимости и
сходимости предложенного алгоритма нахождения решения задачи (6)-(9) дает
Теорема 1. Пусть 
-матрица 
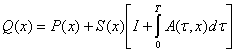обратима для всех 
и
выполняются неравенства:
а) 
;
б) 
,
где
- единичная матрица размерности 2, 
- положительная,
непрерывная по 
функция, 
, 
- const.
Тогда
четверка последовательности 
, 
, определяемая по
построенному алгоритму, равномерно сходится
к четверке функций 
- единственному
решению задачи (6)-(9) для всех 
.
Из эквивалентности задач (1)-(5) и (6)-(9) следует
Теорема 2. Пусть 
-матрица 
обратима для всех 
и
выполняются неравенства а), б) теоремы
1.
Тогда
нелокальная краевая задача для дифференциального уравнения в частных
производных четвертого порядка (1)-(5) имеет единственное решение 
.
Список литературы
1. Gutman S., Ha J., Lee S. Parameter
identification for weakly damped shallow arches // Journal of Mathematical Analysis and
Applications, - 2013. Vol. 403. – pp. 297-313.
2. Wang Ya., Wang Yu. On the
initial-boundary value problem for fourth order wave equations with damping,
strain and source terms // Journal of Mathematical Analysis and
Applications, - 2013. Vol. 405. – pp. 116-127.
3. Kerker M.A. On the Cauchy problem for a
class of iterated Fuchsian partial differential equations // Journal of Mathematical Analysis and
Applications, - 2014. Vol. 414. – pp. 99-109.
4. Holmes J. Continuity properties of
the data-to-solution map for the
generalized Camassa-Holm equation // Journal of mathematical Analysis and
Applications, - 2014. Vol. 417. – pp. 635-642.
5.
Asanova A.T., Dzhumabaev D.S. Unique
Solvability of the Boundary Value Problem for Systems of Hyperbolic Equations
with Data on the Characteristics // Computational Mathematics and Mathematical
Physics. - 2002. - Vol.42. No 11. - pp. 1609-1621.
6. Asanova A.T., Dzhumabaev D.S. Criteria of
well-posed solvability of boundary value problem for system of hyperbolic
equations (Russian) // Izvestia NAN RKazakhstan. Ser. phyz.-mathem. - 2002. No
3. - pp. 20-26.
7.
Asanova A.Т. Analogy of two-point boundary value
problem for systems of hyperbolic equations //Vestnik MES, NAN
RK. -2002. No 1. -pp.81-88.
8. Asanova
A.T., Dzhumabaev D.S. Unique Solvability of Nonlocal Boundary Value
Problems for Systems of Hyperbolic
Equations // Differential Equations. -2003. -Vol. 39. No 10. -pp.1414-1427.
9. Asanova
A.T., Dzhumabaev D.S. Correct
Solvability of a Nonlocal Boundary Value Problem for Systems of Hyperbolic
Equations // Doklady Mathematics. - 2003. - Vol. 68. No 1. - pp. 46-49.
10. Asanova
A.T., Dzhumabaev D.S. Well-Posed Solvability of Nonlocal Boundary Value
Problems for Systems of Hyperbolic Equations //Differential Equations. - 2005.
-Vol. 41. No 3. -pp.352 -363.
11.
Asanova A.T. On the unique
solvability of a nonlocal boundary
value problem with data on
intersecting lines for systems of hyperbolic equations // Differential
equations. -2009. -Vol. 45. No 3.
-pp.385-394.
12.
Asanova A.T. On a boundary-value
problem with data on non-characteristic
intersecting lines for a system of
hyperbolic equations with mixed derivative // Journal of Mathematical Sciences. -2012.
–Vol. 187. No 4.-pp.375-386.
13.
Asanova A.T., Dzhumabaev D.S. Well-posedness of
nonlocal boundary value problems with integral condition for the system of
hyperbolic equations // Journal of mathematical Analysis and Applications, - 2013. - Vol. 402, No 2. pp. 167-178.
14.
Asanova A.T. On multi-point problem
for system of hyperbolic equations with mixed derivative // Nonlinear Oscillations. 2014. Vol. 17,
No 3. pp. 295-313.