УДК 519. 624
Сызықты екі нүктелі шеттік есепті шешудің
бір сандық әдісі
ф.-м.ғ.к. К.Ж.Назарова , оқытушы Б.Ж.Алиханова А Ясауи атындағы ХҚТУ
[0,T] аралығында сызықты екі нүктелі шеттік есепті қарастырайық:
![]() (1)
(1)
![]() (2)
(2)
Мұндағы ![]() - функционалды матрица,
- функционалды матрица, ![]() -вектор функция
-вектор функция ![]() кесіндісінде
үзіліссіз.
кесіндісінде
үзіліссіз. ![]() -тұрақты матрицалар.
-тұрақты матрицалар.
![]()
Шеттік
есептер теориясының зерттелуі көптеген ғалымдардың
еңбектерінде қарастырылған. Жәй дифференциалдық
теңдеулер үшін шеттік есептер
ғылым мен техниканың түрлі есептерін шешуде жиі
кездесетіндіктен бүгінгі күнде де актуальды болып келеді. Мұндай
теңдеулерді шешуде аналитикалық, функционалды –
аналитикалық, сандық
және санды-аналитикалық
әдістер қолданылуда. Түрлі
тәсілдердің қолданылуы түрлі терминдерден
түзілген нәтижелерге алып келеді. Есептеу техникасының
өркендеуі және оның
қолданбалы есептер шешімін табуда қолданылуы жаңа талаптар қоюға
себеп болды. Сондай талаптардың
бірі- әдістің конструктивтілігінде. Конструктивті әдістердің ең негізгі сипаттамасы оның шарттарды
тиімді тексеруі және ақырлы
нәтижесін алуға мүмкіндік беруі. Осындай конструктивті
әдістің бірі - Д.С. Джумабаев[1] ұсынған параметрлеу әдісі.
Бұл әдістің
негізгі мақсаты
дифференциалдық теңдеу қарастырылатын аралық ![]() қадамымен
бөліктерге бөлінеді де бастапқы есеп эквивалентті параметрлі
есепке келтіріледі. Параметрлеу
есебінің шешімі
қадамымен
бөліктерге бөлінеді де бастапқы есеп эквивалентті параметрлі
есепке келтіріледі. Параметрлеу
есебінің шешімі ![]() параметр мен
параметр мен ![]() функция жұбы
жүйесінің тізбектерінің шегі түрінде
анықталады. Параметр
функция жұбы
жүйесінің тізбектерінің шегі түрінде
анықталады. Параметр ![]() шеттік шарттар матрицасы
шеттік шарттар матрицасы ![]() пен дифференциалдық теңдеулер арқылы анықталған
сызықтық теңдеулер жүйесінен, яғни
пен дифференциалдық теңдеулер арқылы анықталған
сызықтық теңдеулер жүйесінен, яғни ![]() теңдеуінен табылады,
ал функция
теңдеуінен табылады,
ал функция ![]() параметрдің табылған мәніндегі
ұзындығы
параметрдің табылған мәніндегі
ұзындығы ![]() аралығындағы интегралдық теңдеудің шешімі.
Параметрдің енгізілуі параметрлеу әдісінің
алгоритмінің жинақталу
шарттары мен қарастырылған есептің шешімінің бар
болуын бастапқы берілімдер терминінде
қамтамасыз етеді.
аралығындағы интегралдық теңдеудің шешімі.
Параметрдің енгізілуі параметрлеу әдісінің
алгоритмінің жинақталу
шарттары мен қарастырылған есептің шешімінің бар
болуын бастапқы берілімдер терминінде
қамтамасыз етеді.
Алгоритм
жинақтылығының, параметрлі шеттік есептің жалғыз шешімі бар болуының
жеткілікті шартын тағайындайтын тұжырымды келтіреміз:
Теорема 1:[7]
Қандай да бір ![]() үшін
үшін ![]() матрицасының
кері матрицасы бар болып келесі
теңсіздіктер орындалсын:
матрицасының
кері матрицасы бар болып келесі
теңсіздіктер орындалсын:
а) ![]()
б) 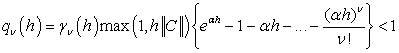
Онда ![]() жұптар тізбегі
жұптар тізбегі ![]() ұмтылғанда көп нүктелі параметрлі шеттік есебінің жалғыз шешімі
ұмтылғанда көп нүктелі параметрлі шеттік есебінің жалғыз шешімі ![]() - ға
жинақталады және келесі бағалау дұрыс
- ға
жинақталады және келесі бағалау дұрыс
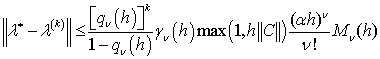 (3)
(3)
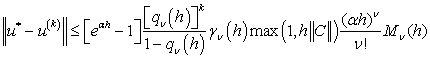 (4)
(4)
Бастапқы (1), (2) есебі мен көп нүктелі шеттік есептің
эквиваленттілігінен теорема 1- ден келесі тұжырым алынады:
Теорема 2:[7] Теорема 1 шарттары орындалсын. Онда (1) –
(2) есебінің жалғыз шешімі ![]() бар болады және
келесі бағалау дұрыс.
бар болады және
келесі бағалау дұрыс.
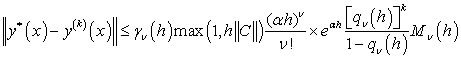 (5)
(5)
Мұндағы ![]() функциясы
функциясы ![]() кесіндісінде үзіліссіз
дифференциалданатын функция.
кесіндісінде үзіліссіз
дифференциалданатын функция.
![]()
функциясы ![]() интервалында
интервалында ![]() функциясының
сығылымы болады.
функциясының
сығылымы болады.
Кейбір
![]() үшін
үшін ![]() матрицасына кері матрицаның бар болуы
бірмәнді шешілімдіктің негізгі шарттарынаң бірі болып
табылады.
матрицасына кері матрицаның бар болуы
бірмәнді шешілімдіктің негізгі шарттарынаң бірі болып
табылады. ![]() матрицасының арнайы
құрылымы бар болғандықтан
матрицасының арнайы
құрылымы бар болғандықтан ![]() кері матрицасының элементтерін есептеп
шығаруға болады.
кері матрицасының элементтерін есептеп
шығаруға болады.
Лемма 1. ![]() матрицасына кері матрица бар болғанда ғана
матрицасына кері матрица бар болғанда ғана ![]() матрицасына кері матрица бар болады.
матрицасына кері матрица бар болады.
Лемма 2. M матрицасының
кері матрицасы ![]() болсын. Онда
болсын. Онда ![]() , матрицасының блоктық элементтерін рекуренттік
формулалар арқылы табамыз:
, матрицасының блоктық элементтерін рекуренттік
формулалар арқылы табамыз:
![]()
![]() ,
, ![]()
![]()
![]()
Есеп. ![]() кесіндісінде екінші ретті дифференциалдық
теңдеу үшін екі нүктелі шеттік есепті
қарастырайық:
кесіндісінде екінші ретті дифференциалдық
теңдеу үшін екі нүктелі шеттік есепті
қарастырайық:
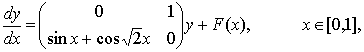 (6)
(6)
![]() ,
, ![]() (7)
(7)
мұндағы
![]() ,
, ![]() ,
, 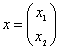
![]() қадамын алып, осы бойынша
қадамын алып, осы бойынша ![]() аралығын бөліктеу жасаймыз
аралығын бөліктеу жасаймыз
![]()
![]() интервалындағы
интервалындағы ![]() функциясының
сығылуын
функциясының
сығылуын ![]()
деп
белгілейміз. ![]() белгілеулер енгізіп
белгілеулер енгізіп ![]()
![]()
![]()
![]() интервалдарында
интервалдарында
![]()
![]()
![]() алмастыруларын жасаймыз. Сонда (6), (7) есебі эквивалентті,
көпнүктелі параметрлі
шеттік есепке келтіріледі.
алмастыруларын жасаймыз. Сонда (6), (7) есебі эквивалентті,
көпнүктелі параметрлі
шеттік есепке келтіріледі.
![]()
![]()
(8)
![]() , (9)
, (9)
![]() (10)
(10)
Вольтердің ІІ текті интегралдық
теңдеуінен
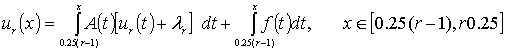 (11)
(11)
бастапқы шарттар арқылы ![]() функцияларын
анықтауға болады. Интегралдық теңдеудің (11) оң жағын (9),
(10) шарттарына қойып белгісіз параметр
функцияларын
анықтауға болады. Интегралдық теңдеудің (11) оң жағын (9),
(10) шарттарына қойып белгісіз параметр ![]() ге байланысты теңдеулер жүйесін аламыз. Теңдеудің
сол жағына сәйкес келетін матрицаны
ге байланысты теңдеулер жүйесін аламыз. Теңдеудің
сол жағына сәйкес келетін матрицаны ![]() , оң жағын
, оң жағын ![]() деп
белгілейміз, сонда мынадай
сызықты теңдеулер жүйесін аламыз
деп
белгілейміз, сонда мынадай
сызықты теңдеулер жүйесін аламыз
![]() (19)
(19)
мұндағы:
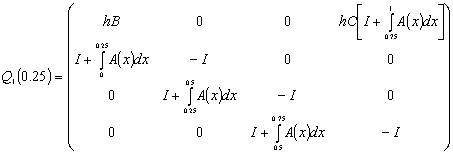
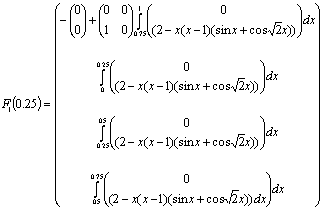
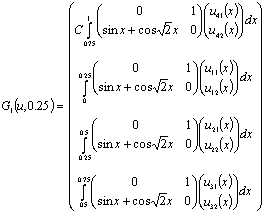
Теорема шарттарына тексеру
үшін ![]() кері матрицасының элементтерін рекуренттік
формулалар арқылы анықтаймыз. Сонда
кері матрицасының элементтерін рекуренттік
формулалар арқылы анықтаймыз. Сонда
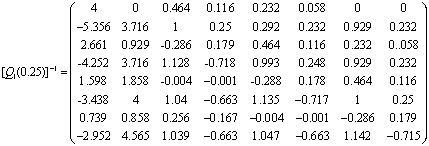
Есептің бірмәнді
шешілімділігі бар жоғын анықтау үшін 1-теореманың
шарттарына тексереміз:
1) ![]()
2) ![]()
![]()
Теореманың екі шарты да
орындалатындықтан (8), (10) есебі бірмәнді шешілімді болып табылады. Демек
(6), (7) есебі де бірмәнді шешілімді.
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ
1.
Джумабаев Д.С. Признаки
однозначной разрешимости линейной
краевой
задачи для обыкновенного дифференциального уравнения// Ж.
вычисл. матем. и матем. физ. -1989. –Т. 29. №1.-С. 50-66.