УДК 531:51-72

ЧИСЛЕННО-АНАЛИТИЧЕСКИЕ МЕТОДЫ РЕШЕНИЯ МОДЕЛЕЙ ДИНАМИКИ МЕХАНИЧЕСКИХ КОНСТРУКЦИЙ

М.Д. КОШАНОВА, Ж.С. ЕРКИШЕВА МКТУ им А.Ясави

Изучаются обобщенная методика определения критических резонансных значения динамики механических конструкций. Они описываются через дифференциальные уравнения с граничными условиями. Решая эти дифференциальные уравнения с граничными условиями, мы опредляем собственные значения, т.е. критические резонансные значения.

1 Сжатый стержень на упругом основании

Пусть стержень длины , подвергающийся действию осевой сжимающей силы величины , лежит на упругом основании (железнодорожный рельс). Примем гипотезу Винклера о том, что сила , действующая на единицу длины стержня при прогибе на величину , пропорциональна величине прогиба ,т.е.

.

называется коэффицентом постели. Тогда при малом продольном изгибе (рисунок 1.6) уравнение упругой линии имеет вид

.

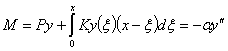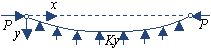
Рисунок 1 - Сжатый стержень на упругом основании

Дифференцирование дает

,

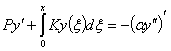и в результате повторного дифференцирования получаем дифференциальное уравнение

. (1.6)

Краевые условия при шарнирном закреплении имеют вид

, .

В следующей проблеме из техники возникает краевая задача, решение которой не вырождается через элементарные функций.

2 Изгибные колебания стержня

Стержень длины с прямолинейной осью, закрепленный каким нибудь образом, например защемленный одним концом, как на рисунке 1.16. крутильных колебаний, также совершать изгибные колебания. Пусть ось совпадает с прямой осью стержня, а ось направлена в сторону предпологаемого отклонения от положения равновесия; отклонение полагается малым.

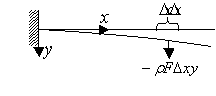
Рисунок 2 - Колебания изгиба защемленного стержня

Рассмотрим вначале колебательный процесс при условии, что каждый элемент стержня колеблется как твердая частица параллельно оси . Остаются неучтенными, таким образом, все побочные влияния, обусловленные тем, что в действительности из-за изменения наклонов упругой линии при колебаниях каждый элемент стержня поворачивается с некоторым угловым ускорением и что элементы стержня не сохраняют свою форму и вследствие изменения углов возникают напряжения сдвига и т.д. Рассматривая затем при обычных обозначениях (плотность , площадь сечения , жесткость на изгиб ) силу инерции - в качестве нагрузки , из известного уравнения изгиба стержня

непосредственно получим уравнение движения

. (1.34)

Отсюда, взяв решение уравнения для собственных колебаний в виде

,

получим обыкновенное дифференциальное уравнение

. (1.35)

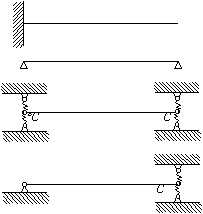
Рисунок 3- Различные виды закрепления колеблющегося стержня

В зависимости от вида закрепления концов стержня имеем различные краевые условия; выделим несколько примеров (рисунок 2).

1. Стержень слева защемлен, справа свободен: , .

2. Стержень закреплен с обеих сторон шарнирно:, .

3. Осуществлено с обеих сторон упругое закрепление стержня.

Здесь при опускании левого конца стержня на величину возникает поперечная сила (где - коэффициент жесткости пружины), следовательно, на левом конце . На правом конце возникает опорная реакция . Таким образом, имеем краевые условия: , , , .

4. Стержень слева закреплен шарнирно, справа – упругое закрепление:

, , .

3 Примеры и численные расчеты на определения критических резонансных значения

1. Опертый на концах стержень длины l с постоянной жесткостью на изгиб и постоянной массой на единицу длины нагружен на расстоянии от опоры массой (рисунок 4) (мотор на балке). Составить трансцендентное уравнение для собственных частот изгибных колебаний (как в пункте 2, пренебрегая побочными влияниями, например продольными колебаниями и т.д.).

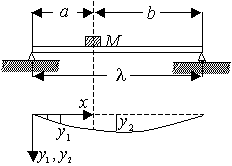
Рисунок 4 - Колебания изгиба балки с сосредоточенной нагрузкой

Решение. Если обозначить прогиб в левом пролете , в правом , то при функции

,

удовлетворяют дифференциальному уравнению и краевым условиям. Постоянные исключаются при помощи переходных условий:

; ; ;

.

Обозначая , получаем для характеристическое уравнение

.

Для получается более простое уравнение

2. Призматический стержень длины , закрепленный на концах, как показано на рисунке 5 в середине и на правом конце подвергается действию осевой силы , т.е. значение, при превышении которого наступает потеря устойчивости при продольном изгибе.

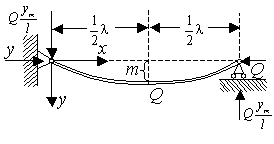
Рисунок 5 - Задача о продольном изгибе стержня при наличии двух

сжимающих сил

Решение. Поскольку стержень имеет постоянную жесткость на изгиб , дифференциальное уравнение упругой линии в каждом из двух пролетов слева и справа от срединной нагрузки можно проинтегрировать в замкнутом виде при помощи тригонометрических функций; исключение постоянных интегрирования из краевых и переходных условий дает для величины трансцендентное уравнение

.

Первые два корня , соответствующие собственным значениям, были приближенно вычислены способом, отличным от приведенного здесь, в работе:

, .

Использованные литературы

1. Коллатц Л. Задачи на собственные значения с техническими приложениями. -М.: Наука, 1968. -504с.

2. Кангужин Б.Е., Кошанова М.Д. О теореме единственности и существования решения нелокальной по времени задач для уравнения

типа С.Л.Соболева // Известия НАН РК. – 2010. -№ 1. -С. 4-10.