Математика/4.Прикладная математика.

Ысмагул Р.С. , ф.-м. ғ.к., доцент,

Даулеткалиева А., Математика мамандығының 1 курс студенті

Қостанай мемлекеттік университеті, Казахстан

Сызықтық дифференциалдық теңдеулер жүйесінің периодты шешімдерін табу

Сызықтық дифференциалдық теңдеулер жүйесін қарастырайық

(1)

мұндағы F(t) — периоды w үзіліссіз периодтық матрица

— (1) дифференциалдық теңдеулер жүйесінің фундаментальды шешімдер жүйесі болсын және ол келесі бастапқы берілгендерді қанағаттандырсын

(2)

мұндағы - п ретті бірлік матрица.

Бағандары болатын квадрат матрицаны фундаментальды шешімдер жүйесінің матрицасы деп атайды.

F(t) периодтық матрица болғандықтан, функциялары да фундаментальды шешімдер жүйесін құрады. Демек, әрбір функциясы коэффициенттері тұрақты функцияларының сызықтық комбинациясы болады. Яғни

Z(t + w) = Z(t)C, (3)

мұндағы Z(t) — шешімдерінің фундаментальды матрицасы, ал — тұрақты матрица.

(1) мен (2) ден Z(t) матрицасы Ż = F(t)Z, Z(0) = E шарттарын қанағаттандыратыны шығады.

(3) теңдігінен t = 0 болғанда Z(w) = C теңдігін аламыз.

Демек, Z(t + w) = Z(t)Z(w). (4)

Z(w) матрицасы (1) теңдеулер жүйесінің монодромии матрицасы деп аталады. çZ(w)ç ¹ 0 болатыны айқын. Z(w) матрицасының меншікті мәндерін (1) теңдеулер жүйесінің мультипликаторлары деп аталады. Сонымен, монодромии матрицасы деп бастапқы берілгендермен анықталған Z(w) матрицасының t= периодындағы мәнін айтуға болады, ал мультипликатор келесі теңдеудің түбірлері деп түсінуге болады

Бұл теңдеу - (1) теңдеулер жүйесінің сипаттауыш теңдеуі [1, с. 59].

(1) біртекті теңдеулер жүйесінің периоды -ға тең нөлдік емес шешімінің бар болуы үшін оның мультипликаторларының біреуі бірге тең болуы қажетті және жеткілікті болып табылады

Мысал. Екінші ретті дифференциалдық теңдеудің периоды -ға тең периодтты жалғыз шешімі бар болатынын көрсетейік

мұндағы f(t) — периоды -ға тең периодты үзіліссіз функция,

Келесі біртексіз сызықтық дифференциалдық теңдеулер жүйесін аламыз.

, где .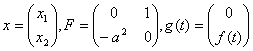

Онда . Яғни, келесі жүйеге келтіреміз 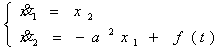(5)

(5) біртексіз жүйесіне сәйкес біртекті жүйенінің фундаментальды матрицасын құрамыз. 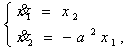(6)

Жүйенің бірінші теңдеуін екінші теңдеуіне қоямыз:

, ал оның сипаттауыш теңдеуі : . Яғни, ,

.

Жалпы шешім келесі түрде жазылады:

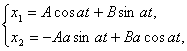
Онда фундаментальды матрица тең:

. Бұдан монодромии матрицасы: (-шарт бойынша).

Әрі қарай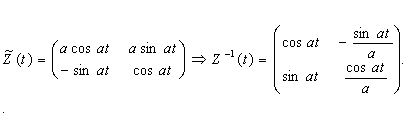

Яғни монодромии матрицасы

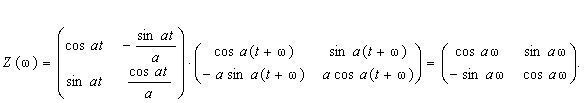
Біртекті жүйенің мультипликаторларын табамыз.

сипаттауыш теңдеу, ал сипаттауыш көпмүшелік келесідей:

онда .

Әдебиет:

8. Самойленко А. М., Кривошея С. А., Перестюк Н. А. Дифференциальные уравнения примеры и задачи. – М.: Высшая школа, 1989, - 384 б.