Философские науки/2. Социальная философия

Д. филос. н. Попов В. В.

Д. филос. н. Музыка О. А.

Д. филос. н. Щеглов Б. С.

Таганрогский институт им. А. П. Чехова (филиал) ФГБОУ ВПО «Ростовский государственный экономический университет (РИНХ)»

Особенности формализованного конструирования момента времени

Исторически преобладающим представлением времени была точка зрения, согласно которой время состоит из множества моментов. Подобная концепция лежит в основе классических парадоксов Зенона, встречается она и в «Элементах» Евклида, где пространственно-протяженное тело ограничено точками и линиями. В современных исследованиях по логике времени под моментом понимается примерно то же, что Евклид понимал под точкой пространства, то есть нечто, не имеющее частей. При этом значительная часть авторов, склоняемся к тому, что понятие момента является достаточно сильной идеализацией. Так, например, А. Прайор считал моменты «искусственными образованиями», а Б. Рассел даже говорил о том, что в некоторых случаях и некоторых сферах исследований моменты будут излишними «метафизическими сущностями». Тем не менее Б. Расселу принадлежит один из возможных способов построения момента времени.

При построении логики процесса удобным является использование момента как неанализируемого и неопределяемого через другие понятия, рассматривая его в аристотелевском смысле как границу интервала времени не имеющую частей. С моментом времени соотносятся состояния объекта, а не события. Эти состояния могут изменяться и тогда в исследовании осуществляется переход от момента к интервалу времени.

Определение 1. Моментной структурой времени называется пара МС=< М, < >, где М – непустое множество (моментов времени); < - бинарное отношение на М (Отношение предшествования).

Минимальный базис структуры МС образуют транзитивное, иррефлексивное и следовательно, асиметричное свойства отношения предшествования, которые универсальны для любой моментной модели времени, определенной на МС.

1. Транзитивность: (x<yÙy<z®x<z)

2. Иррефлексивность: xØ(x<x)

3. Асимметричность: xy(x<y®Ø(y<x))

В случае финитных моделей базисные свойства расширяются принципами конечности и дискретности времени. Принцип конечности постулирует существование начала и конца времени. Дискретность связагна с его онечной делимостью:

4. Конечность: xyØ(x<y)xyØ(y<x)

5.1. Дискретность: xy(x<y®z(x<zØk(x<kk<z)))

5.2. Дискретность: xy(x<y®z(z<xØk(z<kk<y)))

В случае инфинитных моделей необходимым является принцип бесконечности времени, то есть несуществование его начала и конца или принцип плотности внутри временного отрезка, или оба принципа вместе:

6. Бесконечность: xy(x<y)xy(y<x)

7. Плотность: xy(x<y®z(x<zz<y))

Ясно, что инфинитные модели времени могут быть дискретными, если в них выполняется принцип бесконечности, а также конечными в смысле принципа конечности, если в них выполняется принцип плотности, но не тем и другим вметсе.

Темпоральная структура, необходимая для логики изменения должна включать принцип линейности. Линейность времени обычно связывают с философской концепцией детерменизма считая, что данное свойсвто выражает в логической форме однозначно определенную казуальную зависимость последующего состояния. Очевидно, что концепция линейной упорядоченности времени тесно связана с аристотелевской трактовкой изменения во времени как «цепи» актуализированных состояний:

8. Линейность: xy(x<yy<xx=y)

Обратным линейному характеру времени является такое его представление в соответствии с которым время линейно только в направлении к прошлому, но оно ветвится в будущее. Тем самым устанавливается свойство древовидности времени:

9. Древовидность: xyz((y<xÙz<x)®(y=zÚy<zÚz<y))

Данное свойство обычно используется индетерминистской концепцией изменения, которая допускает возможность рассмотрения альтернативных состояний изменяющегося объекта относительно фиксированного момента времени.

Одним из важных свойств моментной структуры времени является направленность временного потока. Данное свойство отражает идею о том, что в потоке времени не существует моментов, которые не связаны между собой отношением предшествования. Для моментной структуры со свойствами бесконечности и линейности свойство направленности выражается в следующих двух принципах, один из которых утверждает о линейной напраленности времени в будущее, а другой в прошлое.

10.1. Направленность: xyz(x<zy<z)

10.2. Направленность: xyz(z<xz<y)

Только принцип 10.2 характерен для древовидной структуры, так как свойство древовидности не предполагает линейность в будущее. Иногда принцип 10.2 в индетерминистских структурах времени называют свойством «связности». Свойства 8, 10.1, 10.2 определяют моментную структуру как координационную систему времени, в которой каждому моменту структуры соответствует определенная точка координаты времени. С подобными точками координат коррелирующих с моментами времени соотносятся состояния изменяющегося объекта. Каждое состояние описывается некоторой формулой или множеством формул. Исходя из этого, можно определить момент так:

Определение 2. m является моментом времени, если и только если m соотносится с множеством формул таких, что:

1) для любой атомарной формулы ¦, либо ¦ соотносится с , либо ئ соотносится с m.

2)

3)

4)

5)

6)

Пусть предикаты P и F имеют общепринятые обозначения «было» и «будет».

7)

8)

9)

10)

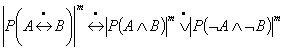
11) – 14) аналогично 7) – 10) (с заменой P на F)

15) если , то

16) если , то

Литература

1. Музыка О.А., Попов В.В. Время и социальная синергетика. – Ростов н/Д: Изд-во ЮФУ, 2007.- 256 с.