УДК 625.768.5.

Базанова Инна Амандыковна – д.т.н, профессор  (Алматы, ЦАУ)

 

 

АНАЛИЗ РАБОТЫ И МЕТОДЫ РАСЧЕТА ЛАВИНОЗАЩИТНЫХ СООРУЖЕНИЙ

 

Стандартное решение системы инженерных сооружений по защите дорог рекомендовать невозможно. Способы защиты от лавин в первую очередь, зависят от значения дороги.

Наиболее эффективным средством защиты дорог с интенсивным движением транспортных средств является комбинация короткого массивного тоннеля с системой легких галерей или сочетание галерей со снегозадерживающими и снегорегулирующими сооружениями. При комплексной защите дорог, народнохозяйственных объектов и ландшафта окружающей среды более эффективными считаются специальные лавинозащитные сооружения из сборных элементов.

За рубежом для этих целей используются специальные железобетонные конструкции, из которых собирают различные типы сооружений.

Инженерные мероприятия по защите автомобильных дорог от снежных лавин могут быть разделены на три основные группы: снегозадерживающие, снегорегулирующие и лавинозащитные.

Чтобы повысить устойчивость снежного пласта и воспрепятствовать его соскальзыванию, выполняют посадку деревьев и кустарников на склонах, рытье канав, террасирование и установку различных задерживающих устройств на склонах – надолб, пирамид, плетневых изгородей, щитов.

На практике часто применяют сборные и монолитные тормозящие устройства с дискретным расположением . Этот класс сооружений защищает отдельно стоящие объекты и гасит кинетическую энергию лавины.

В ряде мест основной причиной зарождения лавин является скопление больших масс снега за счет ветрового снегопереноса и образование мощных снежных карнизов. В таких условиях для уменьшения объема, дальности выброса и предупреждения образования снежных карнизов используются снеговыдувающие щиты, дюзы и кольктафели.

Для пропуска лавин над железными и автомобильными дорогами разработаны многочисленные проекты галерей, эстакад и навесов, которые изготавливались вначале из камня, а затем из бетона, железобетона и дерева. В послевоенные годы преимущественное распространение  получили железобетонные галереи рамной, балочной и консольной (карнизной) конструкций (рисунок 1.).

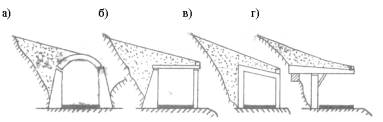
                        а – арочная; б – балочная; в – рамная; г – консольная

Рисунок 1. -  Конструктивные схемы галерей разных типов

 

Несущими элементами галерей являются трехшарнирные ползучие арки и ребристые балки покрытия. Арки расположены шагом 69 м.

Основными методами определения реакций связей являются: статический метод, метод замены связей,  кинематический и графический методы.

Если система геометрически неизменяема и не имеет лишних связей, то она статически определима. Реакции связей в такой системе можно найти способом сечения, используя уравнения равновесия.

 

 

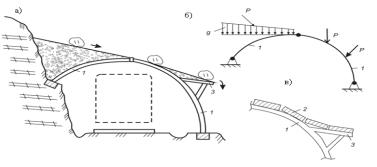
а – общий вид на косогоре; б- расчетная схема; в – фрагмент покрытия

1-криволинейные элементы арки, 2- плита покрытия, 3-консольная часть арки

 

Рисунок 2 – Ползучая арка галерея

В методе замены связей из заданной системы удаляются и заменяются неизвестными реакциями, а на введенные связи  накладываются условия равенства нулю суммарных реакций от действия всех сил.

В кинематическом методе из заданной геометрической неизменяемой системы устраняется связь, реакция которой определяется. Взамен устраненной связи прикладываются соответствующие реакции R.  Система,   таким образом, превращается  в механизм, которому задается возможное перемещение. Затем в соответствии с принципом возможных перемещений составляется выражение работ внешней нагрузки и искомой реакции: ; исходя из которого и определяется значение реакции. Следовательно, неизвестная   R определяется из решения одного уравнения. В этом особенность кинематического метода.

Изложенные аналитические способы представляют некоторые затруднения, если очертание оси арки сложные опоры расположены на разных уровнях, и особенно, если к арке приложены наклонные силы.

В этом отношении графический способ имеет преимущество. Кроме того, графически легко получить кривую давления. При вертикальных же нагрузках ее можно использовать  для построения эпюры моментов.

Существует мнение будто графические построения отличаются недостаточной точностью. Несомненно, что в то время, как арифметические вычисления обычно можно производить с каким угодно количеством десятичных знаков, графические построения имеют какой-то практический предел точности, который невозможно перешагнуть. Однако это соображение не имеет для практики инженерных расче­тов существенного значения, так как при тщательном выполнении чертежа точность получается обычно вполне достаточной (1-2%) .

Во многих задачах строительной механики графический метод вычислений при­меняется не только для изображения окончательных результатов; значение его шире, и он играет роль основного, т. е. вводится в действие не в конце про­цесса решения задачи, а значительно раньше. Его достоинство в этом случае часто состоит не только в наглядности получаемого решения, но и в простоте самих операций, а также в удобном и наглядном контроле, что особенно важно для практики. Наиболее удачные графические решения некоторых задач, полу­чившие широкое применение в строительной механике, отличаются замечательным изяществом и простотой.

История графического метода решения задач  строительной механики весьма своеобразна. Древнейшие работы по механике — Аристотеля (384-321 гг. до н. э), Архимеда (287-212 гг. до н. э.) - в согласии с духом эллинской математики ,  имели геометрический характер.

Когда после долгого перерыва, спустя почти 1800 лет, в Европе возродился интерес к механике, то последняя сначала  также разрабатывалась в значительной     степени  геометрическим   методом.   Таковы,  например,   работы  Галилео   Галилея (1564 -1642 гг.) и труд Ньютона (1642-1727 гг.)  «Математические принципы натуральной  философии» (1687 г.) .

Во второй половине XIX в. появился ряд работ, выдвинувших подлинно гра­фические методы решения ряда задач строительной механики. Важнейшей из них была книга Кульмана (1821-1881 гг.), в которой теория силового и веревочного многоугольников, продвинутая автором несколько дальше, превратилась в метод решения задач о равновесии плоских систем сил.

Значительным расширением графического метода явилось предложенное Мором (1835-1918 гг.) в 1886 г. построение упругой линии простых и неразрезных балок, как веревочных кривых для фиктивной нагрузки.

Следующей важной областью применения графического метода в строительной механике явился так называемый кинематический метод расчета сооружений, который непосредственно связан с графической кинематикой, с нахождением мгновенных центров вращения и построением планов скоростей. Идея метода была дана впервые,  в 1874 г. Мором; затем метод разрабатывался рядом авторов и принял довольно законченную форму в конце 80-х годов.

Для изучения напряженного состояния арки и для суждения о степени рациональности очертания ее оси весьма удобным оказывается использование многоугольника равнодействующих.

Так называется веревочный многоугольник, любая сторона которого направлена по соответствующей равнодействующей всех левых или правых сил. Для арок этот многоугольник называют обычно многоугольником давлений или – в случае сплошной нагрузки – кривой давления.

а) Определение опорных реакций. Предположим что к арке  приложено несколько сил (рис.3) Если имеется распределенная нагрузка, заменим ее сосредоточенными силами.

Сначала найдем равнодействующие  сил приложенных к левой и правой частям арки. Для этого построим силовой многоугольник. Выбрав произвольные полюсы  О1  и  О2 , проведем лучи и построим веревочные многоугольники (показаны пунктиром). Они дадут нам возможность заменить данные нагрузки равнодействующими: Ра – в левой части и Рb  - в правой.

 

 

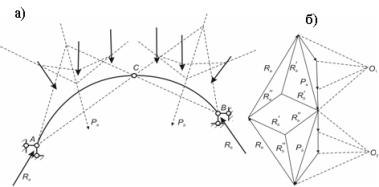
а - схема приведения  к равнодействующей; б – силовой многоугольник

Рисунок 3 -  Определение опорных реакций  в трехшарнирной арке

При определении реакций используем принцип независимости действия сил. найдем сначала реакции  R'a  R'b  только от нагрузки левой части, предполагая правую часть незагруженной. Проведем прямую через В и С до пересечения с силой  Рa  ; полученную точку соединим с А. Начерченные линии дадут направления опорных реакций. Их величины определятся из силового многоугольника проведением параллельных прямых.

Аналогично найдем реакции R"a  и R"b   от нагрузки только правой части.

Далее в силовом многоугольнике построим параллелограмм на си­лах R'b и R"a и сложим силу R'a  с R"a и силу R'b с R"b. В резуль­тате получим полные опорные реакции от нагрузки всей   арки R a  и Rb.

б) Построение кривой давления. Предположим, что опорные реакции для данной арки уже опреде­лены (рис. 4).

Принимая точку пересечения реакций Ra и Rb в силовом много­угольнике за полюс О, построим на чертеже арки веревочный много­угольник, проводя (первый луч через опору А. Этот веревочный мно­гоугольник будет многоугольником давления или кривой давления.

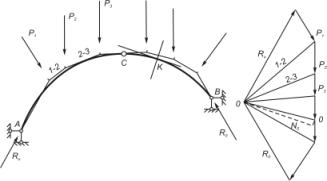
Рисунок12.jpg

 

Рисунок 4 - Построение кривой давления

 

Действительно, луч 1-2 представляет равнодействующую сил Ra и Р1 луч 2-3 - равнодействующую сил Ra, P1  и  P2 и т. д. Таким образом, лучи веревочного многоугольника на чертеже арки непосредственно указывают, через какие точки проходят равнодей­ствующие левых 'сил, а также направления равнодействующих.

Если построение выполнено правильно, то кривая давления, нача­тая от точки А, обязательно должна пройти через средний шарнир С и правый шарнир В. 

в) Поперечные и продольные силы . Лучи силового многоугольника, измеренные в том масштабе, в котором этот многоугольник построен, непосредственно дают величины. равнодействующих в каждом сечении.  Но для получения поперечных и продольных сил необходимо равнодействующие разложить на соответствующие два направления.

Предположим, например, что нужно найти Q и N в сечении   К (рис. 4). Луч силового многоугольника, параллельный лучу веревочного многоугольника, проходящего через сечение К, представляет в масштабе сил равнодействующую левых сил в сечении К.

Проведем через точку К касательную и нормаль к оси арки. Из
концов соответствующего луча силового многоугольника проведем линии, им параллельные. Получим Q и N.  г) ядровые моменты и нормальные напряжения

Нормальное напряжение при внецентренном сжатии имеет наибольшее и наименьшее значения в крайних волокнах сечения. Рассмотрим какое-либо сечение АВ (рис. 5) . Будем считать, что оно имеет по крайней мере одну ось симметрии и что сила N приложена в одной из точек этой оси. Пусть точки КА и КВ  при­надлежат контуру ядра сечения. Как известно, нормальная сила N  вызывает в волокнах сечения нормальные напряжения одного знака или двух знаков в за­висимости  от того, находится ли ее точка приложения  внутри отрезка КА  КВ или в него его.

Обозначим расстояния от точек КА и КВ  до центра тяжести сечения через kA и kB, Если  бы нормальная к сечению сила N была приложена КА то напряжение в волокне А. равнялось бы нулю, следовательно:

,             или                                                  (1)

где    F – площадь сечения,   - момент сопротивления, равный .

Рисунок -5 Схема расположения внутренних усилий и ядро жесткости

 

Сжимающее напряжение в волокне А при расположении силы N, указанном на рис.5 выражается по абсолютной величине  формулой:

;                                                                          (2)

Член  может быть заменен через kA, следовательно,

,                                                                   (3)

                                                                                 (4)

Выражение  есть не что иное, как момент силы N относительно противоположной ядровой точки КА  потому и называются ядровым моментом.

Формула (3) показывает, что наибольшее нормальное напряжение в сечении имеет такое значение, как будто никакой продольной силы   N  нет, а имеется лишь изгибающий момент, равный ядровому моменту . Преимущество этой формулы перед формулой (2)

состоит в том, что она является одночленной и, следовательно, более просто и наглядно выясняющей закон изменения напряжений по оси арки.

 

Литература

 

 

1. Константинов И.А. Динамика гидротехнических сооружений. Расчет плотин на сейсмические воздействия. -  Ленинград,   1976.- Ч. 2.  – 195 с. 

2. Байнатов Ж.Б., Исагулов М.С. Опыт эксплуатации снегозащитных и лавинозащитных сооружений на Серебрянской дистанции пути// Магистраль №8 Алматы 2005 стр. 84-93

3. Базанова И.А. Теория и практика защиты дорог от лавино-оползневых воздействий:  дис. … докт. техн. наук. – Алматы.: КазАТК, 2010. – 317с.

4. Рабинович И.М. Курс строительной механики стержневых систем изд. Госстройлитературы М-Л- 1950, 388с.

       5.Базанова И.А. Основы безопасности жизнедеятельности – Алматы 2013. -387с.