Технические науки/10.Горное дело

К.т.н. Каражанов А.А.

Таразский государственный университет имени М.Х.Дулати,

Республика Казахстан

МОДЕЛИРОВАНИЕ КРИВЫХ 4-ГО ПОРЯДКА С ПРИМЕНЕНИЕМ КВАДРАТИЧНОГО ПРЕОБРАЗОВАНИЯ

Криволинейные поверхности в начертательной геометрии можно получить применив различные геометрические преобразования.

Квадратичные преобразования с вертикальной осью симметрии в начертательной геометрии не использованы. Поэтому данная статья посвящена геометрическому моделированию поверхностей подземных выработок с использованием (2-2)-значных преобразований Д₂, что обеспечивает получить новые криволинейные поверхности по наперед заданным требованиям.

В статье изложено моделирование кривых 4-го порядка с применением преобразования Д₂, когда прообразом представляют собой эллипс, который на плоскости имеет различные расположения. Разработан способ получения новых кривых 4-го порядка с использованием (2–2)-значного преобразования Д₂, который может быть использован в конструировании каналовых поверхностей подземных выработок.

В общем случае эллипс m отображается в кривую 4-го порядка m^' с использованием преобразования Д₂. Уравнение кривой m^' определяется следующим образом:

1. Уравнение прообраза m записывается в виде

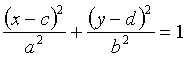. (1)

2. Уравнения (2-2)-значного преобразования Д₂ пишется в виде:

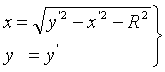, (2)

где ,- координаты точки-образа;

x, y – координаты точки-прообраза;

R – параметр преобразования.

3. Значения х и у из системы уравнений (2) подставив в уравнение (1), получим формулу кривой m^' в виде:

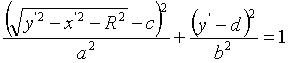, (3)

где х^' , у^' – координаты точек образа m^';

a, b, c, d – параметры прообраза;

R – параметр преобразования Д₂.

Ниже рассмотрим примеры получения новых кривых m^' с использованием преобразования Д₂, когда прообразом является эллипс.

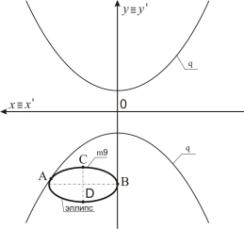
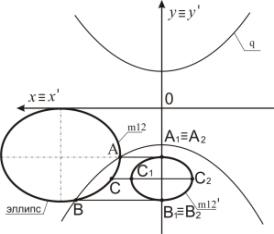
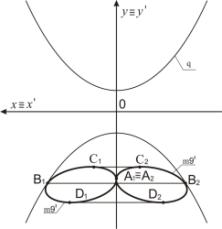
Пример 1. На рисунке 1 эллипс m9 касает ось Оy. Точка А преобразуется в точку А₁ ≡ А₂ с применением преобразования Д₂. Точка В преобразуется в точки В₁ и В₂. Точка D отображается в точки D₁ и D₂. Эллипс m9 преобразуется в две кривые 2-го порядка m9^' (рисунок 2).

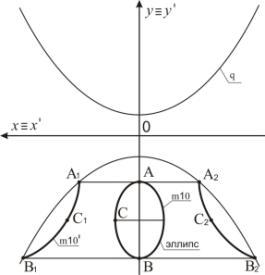
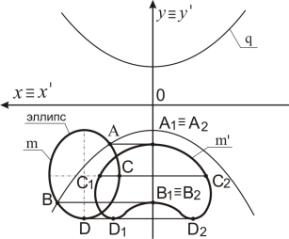
Пример 2. На рисунке 3 одна ось эллипса m10 расположена на оси Оy. Точка А преобразуется в точки А₁ и А₂. Точка С отображается в точки С₁ и С₂. Точка В отображается в точки В₁ и В₂. Эллипс m10 преобразуется в две кривые 2-го порядка m10^' (рисунок 3).

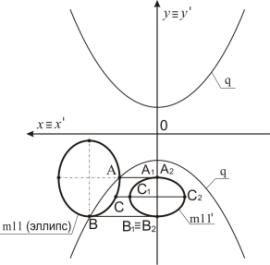
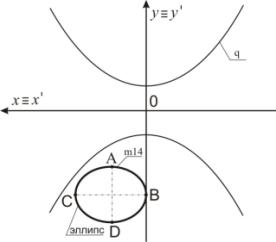
Пример 3. На рисунке 4 задан эллипс m11, который пересекает граничную кривую q в двух точках. Точка А преобразуется в точку А₁ ≡ А₂ с использованием преобразования Д₂. Точка С отображается в точки С₁ и С₂. Точка В преобразуется в точку В₁ ≡ В₂. Эллипс m11 преобразуется в кривую 2-го порядка m11^' (рисунок 4).

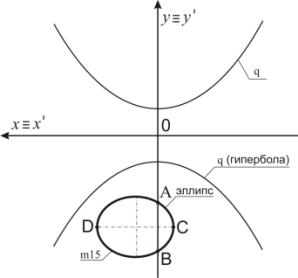
Пример 4. На рисунке 5 длинная ось полученного образа m15^' перпендикулярна к оси Оy. При этом точка В отображается в точку В₁≡В₂. Точка С преобразуется в точки С₁ и С₂. Точка А отображается в точку А₁ ≡ А₂.

Пример 5. На рисунке 6 эллипс m13 преобразуется в кривую 4-го порядка m13^' с использованием преобразования Д₂. При этом точка А отобра-жается в точки А₁ и А₂. Точка К преобразуется в точки К₁ и К₂. Точка D ото-бражается в точки D₁ и D₂. Точка В преобразуется в точку В₁ ≡ В₂ (рисунок 6).

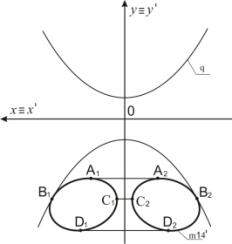
Пример 6. На рисунке 7 прообраз m14 касает ось Оy и не пересекает графическую кривую q. Эллипс m14 преобразуется в две кривые второго порядка m14^' с использованием преобразования Д₂ (рисунок 8). При этом точка А отображается в две точки А₁ и А₂. Точка D преобразуется в точки D₁ и D₂. Точка В отображается в точки В₁ и В₂. Точка С преобразуется в точки С₁ и С₂.

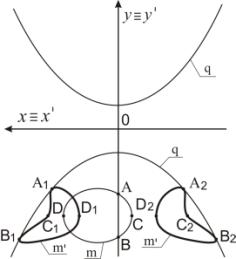
Пример 7. На рисунке 9 заданный прообраз m15 пересекает ось Оy в двух точках. Точки эллипса m15 подвергаем преобразованию Д₂. Точка А преобразуется в точки А₁ и А₂, точка В - в точки В₁ и В₂, точка С - в точки С₁ и С₂, точка D - в точки D₁ и D₂. Эллипс m15 преобразуется в кривую 4-го порядка m15^' (рисунок 10).

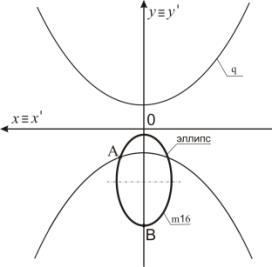
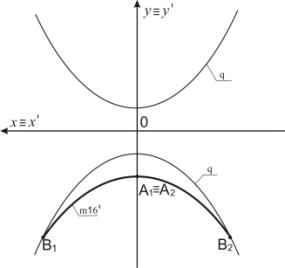
Пример 8. На рисунке 11 большая ось прообраза m16 расположена на оси Оy. Каждую точку пробраза m16 подвергаем преобразованию Д₂. При этом точка А отображается в точку А₁ ≡ А₂. Точка В преобразуется в точки В₁ и В₂. Эллипс m16 преобразуется в вырожденную кривую 4-го порядка m16^' (рисунок 12).

Рисунок 1 – Заданный прообраз m9	Рисунок 2 – Полученный образ m9^'
Рисунок 3 – Преобразование прообраза m10	Рисунок 4 – Преобразование прообраза m11
Рисунок 5 – Преобразование прообраза m12	Рисунок 6 – Преобразование прообраза m13
Рисунок 7 – Заданный прообраз m14	Рисунок 8 – Полученный образ m14^'
Рисунок 2.3.19 – Заданный прообраз m15	Рисунок 2.3.20 – Полученный образ m15^'
Рисунок 2.3.21 – Заданный прообраз m16	Рисунок 2.3.22 – Полученный образ m16^'

Рассмотренные в статье множество примеров показывает характер изменения формы образа, когда прообраз занимает различные положения на плоскости.

Разработанный способ задания (2–2)-значного преобразования Д₂ позволяют использовать это квадратичное преобразование в начертательной геометрии.

Литература

1 . Михайленко В.Е., Кислокий А.А. и др. Геометрическое моделирование и машинная графика. – Киев.: Вища школа, 1991. - 373с.

2 . Нурмаханов Б.Н., Усупов М.М. Разработка способа задания (1-4)- значных преобразований и их применение в построении кривых. – Алматы: Поиск, 1997. - №1.

3 . Байдабеков А.К. Теория нелинейных преобразований и их применение в науке и технике: автореф. … докт. техн. наук:.05.01.01. – М., 2006. – 36с.

4 . Усупов М.М. Разработка и применение (1-4) – значных геометрических преобразований специального вида: автореф. … канд. техн. наук:.05.01.01. – Алматы: КазНТУ, 2004. – 16 с.