Техническая наука/Механика

Таспаганбетов Д.А.

Евразийский национальный университет им. Л.Н.Гумилева, Казахстан

Анализ результатов расчета двухфазных потоков в трубе с изменяющимся сечением

 

Во многих процессах химической технологии – абсорбции, ректификации, экстракции и т. д. происходит движение двухфазных потоков, в которых одна из фаз является дисперсной, а другая — сплошной. Дисперсная фаза может быть распределена в сплошной в виде частиц, капель, пузырей, струй или пленок. В двухфазных потоках первого рода сплошной фазой является газ или жидкость, а дисперсной — твердые частицы, форма и масса которых при движении практически не меняется. В потоках второго рода газ или жидкость образуют и сплошную, и дисперсную фазы. При движении частиц дисперсной фазы в сплошной они могут менять форму и массу, например вследствие дробления или слияния пузырей и капель, что делает математическое описание таких процессов чрезвычайно сложным. 

Знание законов и особенностей двухфазного течения играет первостепенную роль в разработке и совершенствовании технологических процессов, технических установок и устройств в ряде отраслей промышленности, что и определяет актуальность исследований двухфазных потоков и их значимость. Имеется достаточное количество статей, монографии, материалов конференций, посвященное исследованию двухфазных потоков [1]-[10] и т.д.

В этой работе мы проведем анализ взаимозависимости параметров двухфазных течений, опираясь на работу авторов Н.И. Клюева и Е.А. Соловьевой [3], где получена математическая модель кольцевого течения, и выполнены численные расчеты параметров течения. Рассмотрены математические модели кольцевых течений, дисперсных потоков с твердыми включениями, а также критические режимы этих течений. Сформулированы краевые задачи о движении испаряющейся капли в потоке газа и течении пароводяной смеси в обогреваемом цилиндрическом канале. Проведем небольшой анализ полученных математических моделей и взаимозависимость параметров течения.

Пусть даны следующие входные данные: восходящая двухфазная смесь состоит из пара и воды при температуре , плотность газа вязкость газа плотность капли жидкости и плотность жидкости в пленке вязкость капли жидкости и вязкость жидкости в пленке , радиус канала , концентрация легкой фазы , жидкость в пленку подается принудительно с расходом . Расчетные данные этой модели приведены в таблице 1.

Таблица 1

№
1	1.4	0.153	0.168	9.879	0.289	-0.675	0.85	114
2	1.8	0.140	0.115	9.868	0.405	-0.647	1.09	114
3	2.0	0.134	0.085	9.861	0.467	-0.637	1.21	114
4	2.2	0.127	0.052	9.854	0.533	-0.630	1.33	114
5	2.4	0.121	0.017	9.846	0.601	-0.627	1.45	114
6	4.0	0.078	-0.38	9.762	1,184	-0.620	2.40	114

Используя данные вышеуказанной таблицы, рассмотрим взаимосвязь между радиусом пленки и средней скорости жидкости.

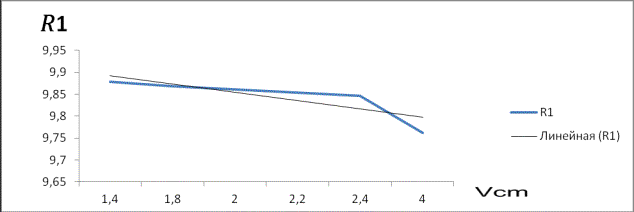
График 1

Из графика 1 следует, что радиус пленки линейно зависит от средней скорости жидкости. А также с увеличением средней скорости смеси радиус смеси уменьшается, а толщина пленки увеличивается линейно.

Используя данные приведенные в Таблице 1, рассмотрим зависимость напряжение трение на границе раздела фаз от средней скорости жидкости.

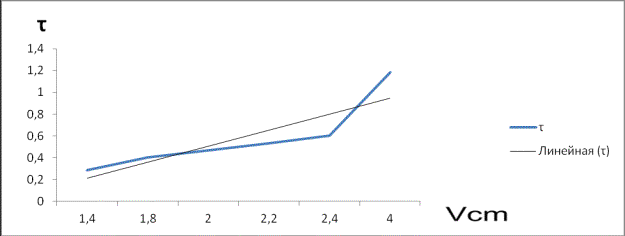
График 2

Из графика 2, можно увидеть, что с увеличением средней скорости смеси напряжение трение на границе раздела фаз возрастает линейно.

Из таблицы 1 и из графиков 1, 2 следует, что с ростом скорости встречного потока скорость жидкости в пленке, а также скорость на поверхности пленки уменьшаются; трение на межфазной поверхности и толщина пленки увеличиваются. Числа Рейнольдса показывают, что поток турбулентный, а пленка ламинарная.

Рассмотрим задачу, когда турбулентный поток смеси и ламинарная пленка жидкости двигаются по цилиндрическому каналу вниз. Результаты численного расчета (температура , радиус канала , концентрация легкой фазы , расход жидкости в пленке  ), полученные в работе [3] , представлены в таблице 2.

Таблица 2

№
1	0.5	0.198	0.314	9.907	-0.101	-0.84	3.04	114
2	1.0	0.214	0.357	9.914	-0.235	-0.92	6.09	114
3	1.5	0.235	0.412	9.921	-0.422	-1.04	9.15	114
4	2.0	0.260	0.474	9.929	-0.657	-1.22	12.21	114

Построим график зависимости радиуса пленки от средней скорости смеси.

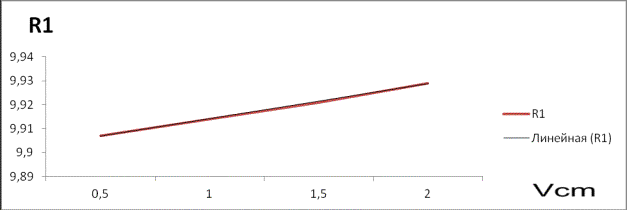
График 3

Из графика видно, что если средняя скорость смеси увеличивается, радиус смеси также увеличивается, а радиус пленки уменьшается линейно.

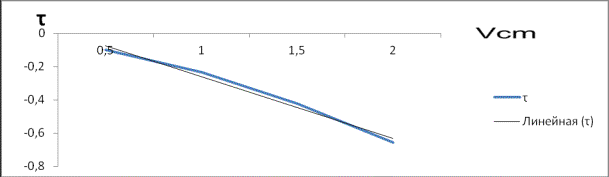
График 4

Из графика следует, что в вертикальном цилиндрическом канале, когда средняя скорость смеси направленно вниз, с увеличением средней скорости смеси напряжение трение на границе раздела фаз уменьшается линейно.

Также необходимо учесть, что расход жидкости в пленке остается постоянным для всех режимов течения. Из таблицы следует, что увеличение скорости смеси разгоняет поверхностные слои жидкости в пленке, трение на межфазной поверхности возрастает (по модулю), толщина пленки уменьшается. Числа Рейнольдса показывают, что поток турбулентный, а пленка ламинарная.

Литература

1 Рахматулин Х.А. Основы газодинамики взаимопроникающих движений сжимающих сред //Прикладная математика и механика.-1956. –Т.20, N.2.

2 Крайко А.Н., Стернин Л.Е. К теории течений двухскоростной среды с твердыми или жидкими частицами //Прикладная математика и механика.-1965.-T.29, N.3.- C.418-429.

3 Н.И. Клюев и Е.А. Соловьева. Математические модели двухфазных течений. -Самара: Изд. «Самарский университет», -2010. -51с.

4 Лунькин Ю.П., Мымрина В.Ф. Вывод уравнений динамики газовзвеси на основе кинетической теории //Сб. Аэродинамика разреженных газов.-1980. -Т10. -С.103-111.

5 Салтанов Г.А. Сверхзвуквые двухфазные течения.-Минск: Беллоруссия, 1972. -480c.

6 Соу С. Гидродинамика многофазных систем. -М: Наука, 1971.

7 Фомин В.М. Численное моделирование волновых процессов в многофазных средах //Rept. Akad. Wiss. DDR. Zentralinst. Math. and Mech. -1980.-N5.-C.98-108.

8 Шрайбер А.А. Течение трехкомпонентной модели полидисперсной смеси с коагуляцией и дроблением частиц //Сб. Промышленная теплотехника.-1980.-N3. C.14-22.

9 Годунов С.К. и др. Численное решение многомерных задач газовой динамики. –М.: Наука, 1976.- 400 c.

10 Матвеев С.К. Математическое описание обтекания тел потоком газовзвеси с учетом влияния отраженных частиц. // Сб. Движение сжимаемых жидкостей и неоднородных сред. Л., 1982. Вып.7. С. 189 – 201