К.т.н. Каряченко Н.В.

Национальная металлургическая академия Украины

О ВЫНУЖДЕННЫХ ПОПЕРЕЧНЫХ КОЛЕБАНИЯХ КАНАТОВ ГРУЗОТРАНСПОРТИРУЮЩИХ УСТРОЙСТВ С ПОДВИЖНОЙ ИНЕРЦИОННОЙ НАГРУЗКОЙ

Поперечные колебания канатов грузотранспортирующих устройств, несущих подвижную распределенную и дискретную инерционную нагрузку, исследованы при одноволновом представлении решения разрешающих уравнений движения, то есть, при представлении решения в виде одной группы стоячих волн. Такое представление дает неполную, и в большинстве случаев, ошибочную картину протекания динамических процессов, происходящих в таких системах, а именно, колебания в них осуществляются в виде суммы двух групп стоячих волн с одинаковыми частотами, но различными формами и фазами колебаний. Поэтому, при одноволновом представлении решения разрешающих уравнений при любом числе удерживаемых в решении слагаемых, невозможно полностью описать динамические процессы, так как не учитывается вторая группа колебаний, связанная со скоростью движения массовой нагрузки.

В работах, посвященных исследованию поперечных колебаний канатов грузотранспортирующих устройств с подвижной инерционной нагрузкой и учитывающих двухволновой характер процессов, происходящих в них, в основном, рассматриваются решения для систем с равномерно распределенной по длине массовой нагрузкой. В то же время, наличие в ней дискретных масс грузов оказывает существенное влияние на качественную картину и количественные характеристики динамических процессов исследуемых объектов.

В работе рассматриваются вынужденные поперечные колебания канатов грузотранспортирующих устройств, несущих подвижную дискретную и распределенную инерционную нагрузку. Однородное дифференциальное уравнение поперечных колебаний одной из ветвей каната таких устройств может быть записано в следующем виде:

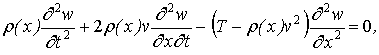(1)

где 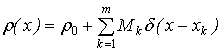, - масса единицы длины каната, - масса к-того сосредоточенного груза, - функция Дирака, - координата, определяющая положение к-того груза, - натяжение каната, - поперечное отклонение, - продольная скорость движения каната.

В силу эллиптичности ведущего барабана или других конструктивных особенностей, в точке набегания каната на барабан возможны периодические поперечные перемещения. В этом случае без нарушения общности, граничные условия запишутся

(2)

где - амплитуда периодического поперечного перемещения, - частота вынуждающего воздействия, - длина пролета.

Как и в работе [2], для удобства построения решения уравнения (1) перейдем к новой функции , связанной с соотношением

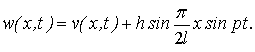(3)

Подставив (3) в (1), после необходимых преобразований получим следующее дифференциальное уравнение

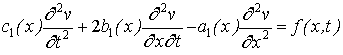, (4)

где

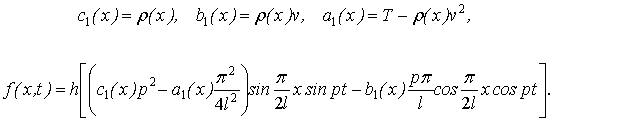
с нулевыми граничными условиями

(5)

Ограничимся исследованием только вынужденных колебаний каната, то есть таких колебаний, которые совершаются под воздействием внешних возмущений, когда начальные возмущения отсутствуют.

Приближенное решение уравнения (4) возьмем как суперпозицию частных решений в виде

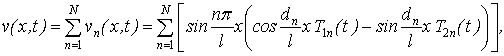(6)

где ,

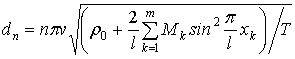- функции, подлежащие определению.

Правую часть (4) представим в виде следующего разложения

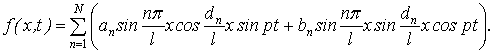(7)

Применяя стандартную процедуру определения коэффициентов разложения и , получим систему алгебраических уравнений, решая которую найдем их выражения (при построении решения данной задачи ограничимся N=2)

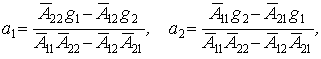
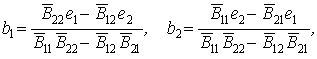
где

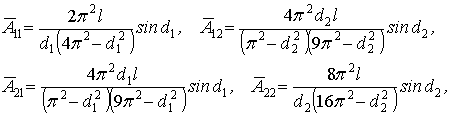
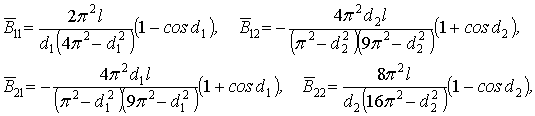
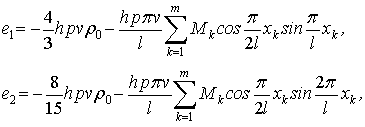
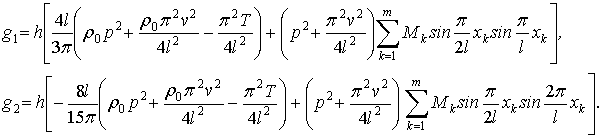
Решение (4) проведем, следуя идее метода Галеркина. После необходимых вычислений, значения функций , определяются по следующим формулам

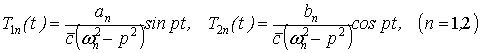. (8)

Подставляя (8) в приближенное решение (6), имеем

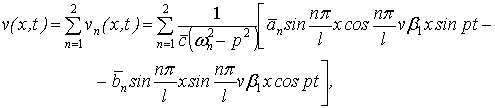
где 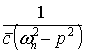– амплитуда вынужденных колебаний,

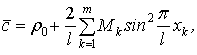
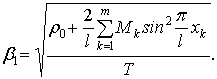
Возвращаясь от функции к функции , получим приближенное решение задачи о вынужденных колебаниях каната, несущего подвижную распределенную и дискретную инерциальную нагрузку

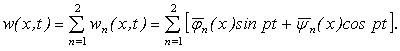
Формы вынужденных и вынужденных "сопровождающих" колебаний определяются выражениями

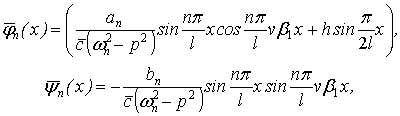
где

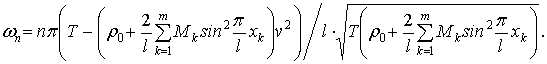
Полученное решение позволяет исследовать поведение системы при прохождении ее через резонанс в зависимости от скорости движения канатов, соотношения между собственной и вынужденной частотой колебаний, количества грузов между опорами, значений их масс и расположения.

Литература:

1. Колесник И.А., Каряченко Н.В. Колебания механических звеньев устройств, несущих подвижную инерциальную нагрузку // 4-й Польско-Украинский семинар “Теоретические основы строительства”.-Том 1.Ч.2. - Днепропетровск: ПГАСУ. - С. 237-241.

2. Титова Л.Д. Исследование задач динамики одномерных упругих объектов с подвижной массовой нагрузкой: Автореф. дис. ... канд. физ.-мат. наук. - Днепропетровск, 1981. - 20 с.