Майлыбаев Е.
– магистр Международного университета информационных технологии
г Алматы, Республика Казахстан
АНАЛИЗ И
ИССЛЕДОВАНИЯ МЕТОДОВ РЕШЕНИЯ ТРАНСПОРТНЫХ ЗАДАЧ
Одна из
самых распространенных и востребованных задач в логистике - транспортная
задача. В классическом виде она предполагает нахождение оптимального (т.е.
сопряженного с минимальными затратами) плана грузоперевозок.
Транспортная
задача (задача Монжа — Канторовича) — математическая задача линейного
программирования специального вида о поиске оптимального распределения
однородных объектов из аккумулятора к приемникам с минимизацией затрат на
перемещение.
Для
простоты понимания рассматривается как задача об оптимальном плане перевозок
грузов из пунктов отправления (например, складов) в пункты потребления
(например, магазины), с минимальными общими затратами на перевозки.
Транспортная
задача (классическая) — задача об оптимальном плане перевозок однородного продукта
из однородных пунктов наличия в однородные пункты потребления на однородных
транспортных средствах (предопределённом количестве) со статичными данными и
линеарном подходе (это основные условия задачи).
Для классической транспортной
задачи выделяют два типа задач:
• критерий стоимости
(достижение минимума затрат на перевозку) или расстояний
• критерий времени
(затрачивается минимум времени на перевозку). Под названием транспортная
задача, определяется широкий круг задач
с единой
математической моделью, эти задачи относятся к задачам линейного
программирования и могут быть решены оптимальным методом.
Математическая
модель транспортной задачи: имеется m пунктов отправленияА1,
А2 , Ат в которых сосредоточены запасы каких-то однородных
грузов в количестве соответственно а1, а2, ... , ат
единиц. Имеетсяn пунктов назначения В1 , В2 , ... , Вп подавшие заявки соответственно на b1 , b2 , ... , bn единиц груза. Известны стоимости Суперевозки единицы
груза от каждого пункта отправления Аідо каждого пункта назначения Вj . Все числа Су, образующие прямоугольную таблицу
заданы. Требуется составить такой план перевозок (откуда, куда и сколько единиц
поставить), чтобы все заявки были выполнены, а общая стоимость всех перевозок
была минимальна.
Задача о
перевозках, в которой сумма запасов ровна сумме заявок:
2Х= Zbj( где i=1,...,m
; j=1,...,n ) (1)
это
классическая транспортная задача, иначе называемая, транспортной задачей: с
правильным балансом, а ее модель — закрытой. Если же это равенство не
выполняется, то задача называется задачей с неправильным балансом, а ее модель
— открытой.
Различают
три вида транспортных задач согласно условию сбалансированности [1]:
•
сбалансированная транспортная задача, в случае, если количество
произведенной продукции равно суммарной потребности в ней;
•
транспортная задача в условиях перепроизводства, в этом случае для
сведения ее к сбалансированной транспортной задаче необходимо ввести фиктивный
пункт потребления, стоимость перевозки единицы продукции в который равен нулю;
•
транспортная задача в условиях дефицита, в этом случае для сведения ее
к сбалансированной транспортной задаче необходимо ввести фиктивный пункт
производства, стоимость перевозки с которого можно принять равной нулю.
Методы решения транспортной задачи
Для
решения транспортной задачи было разработано большое число различных методов и
посвящено множество работ следующих ученых: Ford,
Fulkerson, Munkers, Kuhn,
Gleyzal, Golshtein.
Методы
решения классической транспортной задачи делятся на:
•
Точные методы
•
Приближенные методы
Приближенные
методы, известные также как методы нахождения опорного плана, позволяют за
небольшое число шагов получить допустимое, но не всегда оптимальное, решение
задачи. К данной группе методов относятся методы:
•
вычеркивания
•
северо-западного угла
•
минимального элемента
•
аппроксимации Фогеля
Опорное решение транспортной задачи
Существуют
различные методы решения транспортной задачи. Рассмотрим более конкретно
некоторые из них. Опорным решением транспортной задачи называется любое
допустимое решение, для которого векторы условий, соответствующие положительным
координатам, линейно независимы [2]. Для проверки линейной независимости
векторов условий, соответствующих координатам допустимого решения, используют
циклы.
Циклом
называется такая последовательность клеток таблицы транспортной задачи, в
которой две и только соседние клетки расположены в одной строке или столбце,
причем первая и последняя также находятся в одной строке или столбце. Система
векторов условий транспортной задачи линейно независима тогда и только тогда,
когда из соответствующих им клеток таблицы нельзя образовать ни одного цикла.
Следовательно, допустимое решение транспортной задачи , i=1,2,...,m;
j=1,2,...,n является опорным только в
том случае, когда из занятых им клеток таблицы нельзя образовать ни одного
цикла [3].
Приближенные
методы решения транспортной задачи.
Метод
вычеркивания : Если в строке или столбце таблицы одна занятая клетка, то она не
может входить в какой-либо цикл, так как цикл имеет две и только две клетки в
каждом столбце. Следовательно, можно вычеркнуть все строки таблицы, содержащие
по одной занятой клетке, затем вычеркнуть все столбцы, содержащие по одной
занятой клетке, далее вернуться к строкам и продолжить вычеркивание строк и
столбцов. Если в результате вычеркивания все строки и столбцы будут вычеркнуты,
значит, из занятых клеток таблицы нельзя выделить часть, образующую цикл, и
система соответствующих векторов условий является линейно независимой, а
решение опорным. Если же после вычеркиваний останется часть клеток, то эти
клетки образуют цикл, система соответствующих векторов условий линейно
зависима, а решение не является опорным [4].
Метод
«северо-западного угла»: метод (правило) получения допустимого начального
решения транспортной задачи. Этот метод был предложен Данцигом в 1951 г. [5] и
назван Чарнесом и Купером [6] «правилом северо-западного угла» [7].
Метод
состоит в последовательном переборе строк и столбцов транспортной таблицы,
начиная с левого столбца и верхней строки, и выписывании максимально возможных
отгрузок в соответствующие ячейки таблицы так, чтобы не были превышены
заявленные в задаче возможности поставщика или потребности потребителя. На цены
доставки в этом методе не обращают внимание, поскольку предполагается
дальнейшая оптимизация отгрузок.
Метод
«минимального элемента»: Отличаясь простотой данный метод все же эффективнее
чем, к примеру, метод Северо-западного угла [8]. Кроме того, метод минимального
элемента понятен и логичен. Его суть в том, что в транспортной таблице сначала
заполняются ячейки с наименьшими тарифами, а потом уже ячейки с большими
тарифами. То есть мы выбираем перевозки с минимальной стоимостью доставки
груза. Это очевидный и логичный ход. Правда он не всегда приводит к
оптимальному плану.
Метод
«аппроксимации Фогеля»: При методе аппроксимации Фогеля на каждой итерации по
всем столбцам и по всем строкам находят разность между двумя записанными в них
минимальными тарифами. Эти разности записывают в специально отведенных для
этого строке и столбце в таблице условий задачи. Среди указанных разностей
выбирают минимальную. В строке (или в столбце), которой данная разность
соответствует, определяют минимальный тариф. Клетку, в которой он записан, заполняют
на данной итерации [9].
Точные
методы решения транспортной задачи.
Точные
методы позволяют найти оптимальное решение. Конечные методы решения
транспортной задачи можно ить на группы в соответствии с тем, на каком из
методов решения общей задачи линейного программирования они основываются.
Одна
группа алгоритмов основана на наиболее популярном методе линейного
программирования - методе последовательного улучшения плана, другая базируется
на идеях метода последовательного сокращения невязок [10].
По частоте
применения можно выделить два точных метода решения транспортной задачи [11]
•
метод потенциалов
•
венгерский метод
Метод
потенциалов предназначен для решения транспортной задачи в матричной
постановке. Потенциалы — это двойственные переменные. Сам метод — прямой, на
каждом шаге выбирается одно из двойственных ограничений, которое не выполняется
и исправляется таким образом, чтобы не нарушить ограничения прямой задачи.
Постепенно в двойственной задаче ограничения будут выполнены, что будет
означать оптимальность в прямой задаче. Таблица для метода потенциалов имеет
следующий вид (рис.1) [12]:
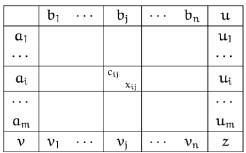
Рисунок-1. Таблица для метода
потенциалов
В случае,
если опорный план содержит меньше ненулевых компонент чем число линейно
независимых уравнений системы ограничений задачи, то такой план называется
вырожденным. В этом случае необходимо внести некоторые коррективы в алгоритм
метода потенциалов. То есть, метод потенциалов чувствителен к вырожденности
задачи, что может оказать существенное влияние на качество решения задач
высокой размерности [13].
Вторым по популярности
является венгерский метод. Идея этого метода была высказана
венгерским-математиком Эгевари задолго до возникновения теории линейного
программирования в 1931 г. Длительное время она оставалась малоизвестной. В
1953 г. американский математик Кун перевел ее на английский язык. Он развил
идею Эгевари и предложил метод, названный им венгерским, для решения задачи
выбора (частный случай, транспортной задачи) [14]. В дальнейшем метод был
усовершенствован и перенесен на произвольную транспортную задачу [15].
Венгерский алгоритм относится ко второй группе конечных алгоритмов. Он не
чувствителен к вырожденности задачи и не требует решения системы линейных
уравнений. С другой стороны его логическая структура сложнее, чем в методе
потенциалов.
СПИСОК ЛИТЕРАТУРЫ
1. Симаков Е. Е. Решение
транспортных задач с применением программирования в системе MathCAD. Казань: Молодой ученый. — 2014. — №5. — С. 8-13.
2.
Абчук В.А., Экономико-математические методы: учебное пособие для вузов.
- СПб.: Союз,1999. - 10 с
3. http://www.grandars.ru/student/vysshaya-matematika/opornoe-reshenie- transportnoy-zadachi.html
4.
Абчук В.А., Экономико-математические методы: учебное пособие для вузов.
- СПб.: Союз,1999. - 13 с
5. Dantzig, G. В., Application of the Simplex Method to a
Transportation Problem, chap. XXIII of // Koopmans T.C. (ed.), Activity
Analysis of Production and Allocation, Cowles Commission Monograph 13, John
Wiley & Sons, Inc., New York, 1951.
6.
Charnes
A. and W. W. Cooper, The Stepping Stone Method of Explaining Linear Programming
Calculations in Transportation Problems, Management Science 1, 1954—1955.
7. С.Гасс. Линейное
программирование (методы и приложения) / Пер. с англ. Гольштейна Е. Г. и
Сушкевича М. И., под ред. Юдина Д. Б. Государственное издательство
физико-математической литературы, Москва, 1961
8. http://www.galyautdinov.ru/post.php?id=14&n=metod-minimalnogo-elementa
9. Балдин К. В., Башлыков В. Н.,
Рукосуев А. В. Математические методы и модели в экономике. М.:Флинта, 2012. С
96.
10.Гольштейн Е.Г., Юдин Д.Б.
Задачи линейного программирования транспортного типа. - М.: Наука, 1969. - 384
с.
11.Дубравина Т.В., Решение
модифицированных транспортных задач металлургического комплекса с
использованием генетических алгоритмов М.: Московский государственный институт
стали и сплавов, 2005г
12.http://www.karavaev.me/teaching/files/AlgoTr.pdf
13.Раскин Л.Г., Кириченко И.О.
Многоиндексные задачи линейного программирования (теория, методы,
приложения).—М.: Радио и связь, 1982.- 240с.
14. Кун (Kuhn H.W.)
Венгерский метод решения задачи о назначениях.
// Сб. "Методы и алгоритмы решения транспортной задачи". -
Госстатиздат, 1963.
15.Манкерс (Munkers J.) Алгоритм решения задачи
выбора и транспортной задачи. //Сб. "Методы и алгоритмы решения
транспортной задачи". - Госстатиздат, 1963, стр.73-79.