Современные
информационные технологии/1.Компьютерная инженерия
К.т.н. Ткаченко В.Г., к.т.н. Ларин Д.Г.
Одесская национальная академия связи
полный перебор остовов в
телекоммуникационной сети с помощью монотонных булевых функций
Для исследования
и оптимизации телекоммуникационных сетей чаще всего применяется аппарат теории
графов. Одним из исследуемых понятий в теории графов является дерево или остов
графа.
Существующие
алгоритмы, такие, как алгоритм построения минимального покрывающего дерева
(остова наименьшей стоимости), предназначены для построения одного остова,
оптимального по какому-либо критерию [1]. Задача получения всех
остовов, которая может возникнуть при отсутствии (неопределенности) весов ребер
графа или при наличии у ребер нескольких весов, соответствующих не связанным
между собой характеристикам (т.е. там, где нет возможности привести весовые
значения ребер к одному параметру) решается методом полного перебора.
Для решения подобной задачи, определения всех остовов графа
исходя из его топологии, предлагается алгоритм.
Пусть задан некоторый связный граф G=(V,Е) V –
множество вершин, Е – множество ребер. Каждому ребру соответствуют
вершины начала и конца. Топологию графа можно задать в виде перечня ребер е1,
е2, е3, … еm, где каждое
ребро описывается совокупностью вершин, которое оно связывает. В итоге получатся
монотонная булева функция (МБФ) инциденции заданая в виде минимальной
дизьюнктивной формы [2]. Для сети на рис 1. эта функция имеет вид (v1v2)Ú(v1v4)Ú(v1v5)Ú(v2v3)Ú(v2v5)Ú(v3v5)Ú(v4v5). Для этой же сети можно
написать более простую МБФ коньюнкции которой соответствуют полным подграфам
или кликам этой сети (v1v2v5)Ú(v1v4v5)Ú(v2v3v5), назовем эту функцию
кликовая МБФ данной сети. Из этой МБФ можно однозначно получить предыдущую.
Также можно описать сеть с помощью ребер, в виде т.н. реберной МБФ (acd)Ú(abe)Ú(bf)Ú(cg)Ú(defg), в данном случае число
коньюнкций равно числу вершин.
Известно, что число ребер в остове графа равняется N-1,
где N – число вершин графа, поэтому возникает необходимость проверки всех
вариантов по N-1 ребру и выделения из них тех, которые являются
остовами.
Выбор
комбинации ребер осуществляется следующим образом: каждое ребро может или
входить в выборку или не входить, то можно обозначит состояние каждого ребра
или как 1 (ребро входит), или как 0 (ребро не входит). Таким
образом, множество ребер графа Е можно представить в виде бинарного
числа, количество разрядов которого равно количеству ребер графа. И последовательно
сдвигая разряд (попарно инвертируя элементы) можно просмотреть все возможные
комбинации. Т.е., решать указанную задачу используя аппарат булевой алгебры.
Например, если задан граф (рис. 1)
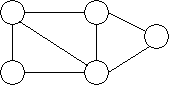 1 a 2
1 a 2
b
c d e 3
f
4 g 5
Рисунок 1 – Пример графа телекоммуникационной сети
то пересмотр комбинаций будет выглядеть следующим
образом (табл.1)
Таблица 1 – Реализация перебора вариантов построения остова
|
№ выборки |
Ребра |
||||||
|
a |
c |
d |
b |
e |
f |
g |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
|
2 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
|
3 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
|
4 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
|
5 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
|
6 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
|
7 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
Продолжение табл. 1
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
8 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
|
9 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
|
10 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
|
11 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
|
12 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
|
13 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
|
14 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
|
15 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
16 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
|
17 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
|
18 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
|
19 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
|
20 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
|
21 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
|
22 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
|
23 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
|
24 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
|
25 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
|
26 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
27 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
|
28 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
|
29 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
|
30 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
|
31 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
|
32 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
|
33 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
|
34 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
|
35 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
Условием того, что выбранная группа ребер является остовом, будет проверка вхождения в него всех вершин. Для данного графа эта проверка будет выглядеть следующим образом:
- условие
наличия вершины 1 в выборке (aÚcÚd)=1;
- условие
наличия вершины 2 в выборке (aÚbÚe)=1;
- условие
наличия вершины 3 в выборке (bÚf)=1;
- условие
наличия вершины 4 в выборке (cÚg)=1;
- условие
наличия вершины 5 в выборке (dÚeÚfÚg)=1;
Т.е. условие
наличия всех вершин в выборке является двойственная функция от приведенной
ранее реберной МБФ
(aÚcÚd)Ù(aÚbÚe)Ù(bÚf)Ù(cÚg)Ù(dÚeÚfÚg)=1.
В [3] показано, что
топологию любой сети можно описать в виде квадриальной четверки МБФ.
Кроме того, т.к. перечень ребер упорядочен по вершинам входящим в него, то невыполнения условия вхождения 1-й вершины в остов служит концом работы алгоритма, т.к. все остальные комбинаций уже не будут содержать ребра, связывающие 1-ю вершину с другими. В данном примере это видно в последней итерации.
Данный алгоритм
позволяет минимизировать перебор комбинаций ребер для построения всех остовов
графа.
Литература
1. Кристофидес Н.
Теория графов: алгоритмический подход / Кристофидес
Н. – М.: Мир, 1978, 430 с.
2. Ткаченко
В.Г. Отказы цифровых схем и представления монотонных булевых
функций / В.Г. Ткаченко //Наукові праці ОНАЗ ім. О.С. Попова. – 2006. – №2. – С. 54 – 69.
3. Иваницкий
А.М. Взаимосвязь между матроидами и монотонными булевыми функциями
электрических цепей/ А.М.Иваницкий, В.Г. Ткаченко, //Наукові праці ОНАЗ ім. О.С. Попова. – 2009. – №1. – С. 18 – 26.