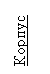Божанов Е.Т., Сатыбалдиев О.С., Назарбаев Д.А., Сагатбек Д.
Казахский национальный технический университет имени К.И. Сатпаева,
Казахстан
Расчетная математическая модель
биомеханики человека с позиции теории неупругой среды механики сплошных сред
под действием статических нагрузок.
Постановка задачи.
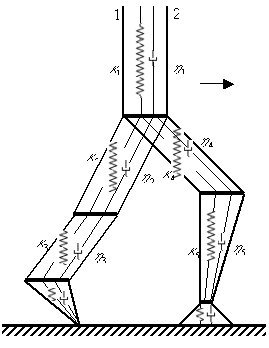
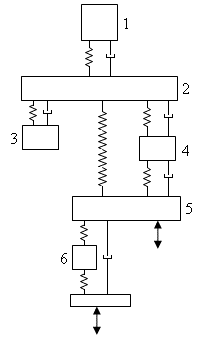
Рассмотрим биомеханику человека с позиции теории неупругой среды механики сплошных сред [1]-[6] как трубчатую конструкцию из упруго-вязких материалов Рис.1-4. Условия равновесия элемента биомеханики человека под действием статических нагрузок на отдельных участках сопряжения имеет вид:
![]()
где ![]() - коэффициент вязкости демпфера,
- коэффициент вязкости демпфера, ![]() - коэффициент
жесткости пружины,
- коэффициент
жесткости пружины,
![]() - активная нагрузка по формам. Критической деформации
поперечного сечения:
- активная нагрузка по формам. Критической деформации
поперечного сечения:
![]() ,
, ![]() ,
, ![]()
![]() ;
;
![]() - внутренний радиус трубчатой конструкции,
- внутренний радиус трубчатой конструкции, ![]() - длина,
- длина, ![]() - толщина,
- толщина,
![]() - гибкость,
- гибкость, ![]() - коэффициент
приведения длины,
- коэффициент
приведения длины, ![]() - наименьший радиус инерции поперечного сечения,
- наименьший радиус инерции поперечного сечения, ![]() - модуль Юнга.
- модуль Юнга.
|
Рис.1 Шагающая модель человека |
Рис.2 Разомкнутая кинетическая цепь руки человека |
|
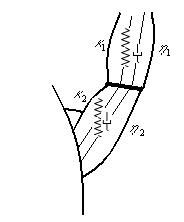
Рис.3 Модель сердца на механической подвеске |
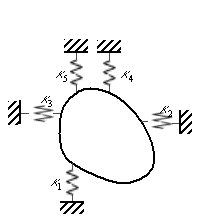
Рис.4 Модель человеческого организма 1-голова, 2-торс, 3-грудная клетка, 4-позвоночный столб, 5-таз, 6-ноги. |
Пусть характеристическое
уравнение:
![]()
имеет два действительных корней и два комплексных корней ![]() ,
,
![]() ;
; ![]() ,
,![]()
где ![]() ,
, ![]() ,
, ![]() .
.
Данное предположение
с точки зрения механики означает, что коэффициент вязкости намного больше
коэффициента сопротивления, т.е. ![]() . Следовательно, вместо дифференциального уравнения в первом
приближении рассмотрим дифференциальное уравнение модели Б-3;
. Следовательно, вместо дифференциального уравнения в первом
приближении рассмотрим дифференциальное уравнение модели Б-3;
![]() (1)
(1)
при тех же граничных условиях
![]() ,
,![]()
![]() ,
, ![]() (2)
(2)
т.е. правый край свободный, а левый край скользящее заделанный.
Решение. Общее решение ищем в виде
![]() (3)
(3)
где ![]() - общее решение однородной части, т.е.
- общее решение однородной части, т.е.
![]() (4)
(4)
где ![]() ,
, ![]() (5)
(5)
![]() - какое-нибудь частное решение (1):
- какое-нибудь частное решение (1):
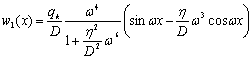 (6)
(6)
На основании (4) и (6) из (3) определим общее решение дифференциального уравнения (1) как линейное перемещение точек деформации человеческого организма:
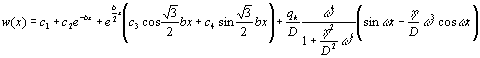 (7)
(7)
При методе сечении условия заключаются в том, что в смежных сечениях, до и после места сопряжения, должны быть одинаковы
- линейные перемещения - ![]() ,
,
- угловые перемещения - ![]() ,
,
- изгибающие моменты - ![]()
- перерезывающие силы - ![]() .
.
Из (7) определим их без множителя:
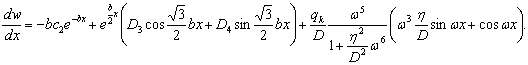 (8)
(8)
где ![]() ,
, ![]() (9)
(9)
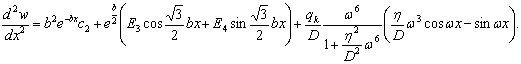 (10)
(10)
где ![]()
![]() (11)
(11)
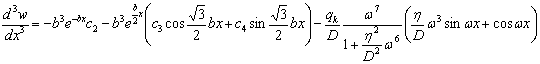 . (12)
. (12)
Произвольные постоянные
интегрирования![]() ,
,![]() ,
,![]() ,
,![]() определим из граничных условии (2).
определим из граничных условии (2).
![]()
![]()
![]() =>
=> 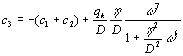 (13)
(13)
![]() =>
=> 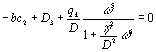 => c учетом (13)
=> c учетом (13)
=> 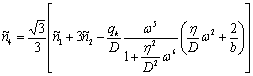 (14)
(14)
![]()
![]()
Из условии ![]() (формула (12)) c учетом (14)
(формула (12)) c учетом (14)
=> ![]() , (15)
, (15)
где ![]() ,
, ![]() ,
,
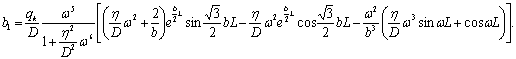 (16)
(16)
![]()
![]()
Из условии ![]() (формула (10)-(11)) =>
c учетом (13) и (14)
=>
(формула (10)-(11)) =>
c учетом (13) и (14)
=>
![]() (17)
(17)
где ![]() ,
, ![]() ;
;
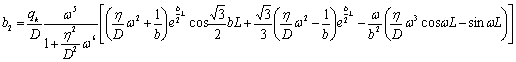 (18)
(18)
Для определения произвольно
постоянных ![]() и
и ![]() интегрирования имеем
систему алгебраических уравнений (15)-(18), которая имеет единственное решение.
Решая данную систему определим:
интегрирования имеем
систему алгебраических уравнений (15)-(18), которая имеет единственное решение.
Решая данную систему определим:
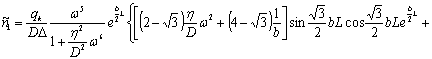
![]()
![]()
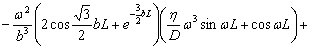
![]() (19)
(19)
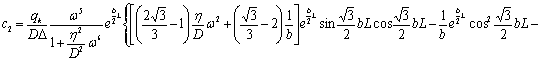
![]()
![]()
![]() , (20)
, (20)
![]() . (21)
. (21)
На основании формул (13) и (14) с учетом (19)-(21) получим:
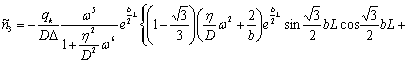
![]()
![]()
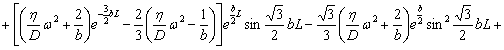
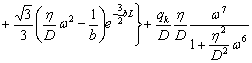 . (22)
. (22)
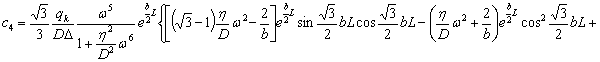
![]()
![]()
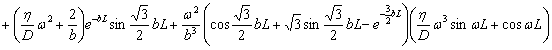
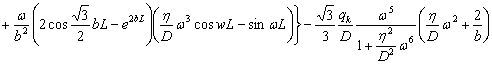 (23)
(23)
Подставляя формулы, значения ![]() , (19)-(23) в формулу (7) получим:
, (19)-(23) в формулу (7) получим:
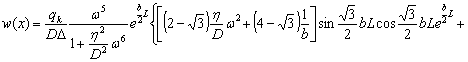
![]()
![]()
![]()
![]()
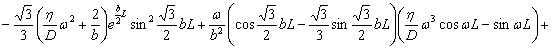
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
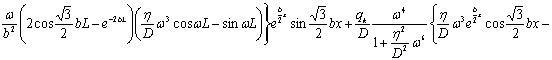
![]() .
.
где ![]() ,
, ![]() ,
, ![]()
![]() .
.
![]()
![]()
![]() .
.
![]()
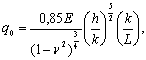
![]() .
.
Литература.
- Е.Т. Божанов, Ж.С. Ержанов, Исследование проблем устойчивости упругих тел, гибких планстин и оболочек, их приложения, Алматы, 2001 г.
- Е. Т. Божанов, А.М. Ибраимкулов, Б.А. Тулешева, Анализ численных результатов устойчивости выработок в толще горных пород под действием поперечных и осевых сил, Актобе, 2007г.
- А.И. Цейтлин, А.А. Кусаинов, Методы учета внутреннего трения в динамических расчетах конструкции, Алматы, 1987 г.
- З.М. Рахимбекова, Нелинейные стержневые системы за пределом упругости, Алматы, 2002 г,
- Р. Глазер, Очерк основ биомеханики: Перевод с нем./ под ред. С.А. Регирера., М, Мир, 1988, 176 с.
- Вибрационная техника: Использование вибрации в биологии и медицине / Под. Ред. К.Ф. Фролова, М., Наука, 1989, 157с.