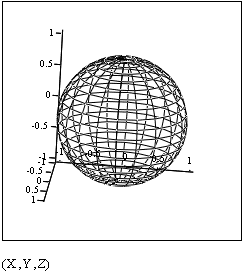
Коспанбетова Н. А., к.ф.-м.н., доцент Нысанов Е.А.
Южно-Казахстанский
Государственный университет, г. Шымкент
ПОСТРОЕНИЕ ГРАФИКОВ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ НА ЯЗЫКЕ ПРОГРАММИРОВАНИЯ И В СРЕДЕ MATHCAD
Сфера. Уравнение
сферы с центром в точке 
и
радиусом R
записывается в таком виде [1]
А уравнение сферы с центрам в начале координаты записываются в этом виде
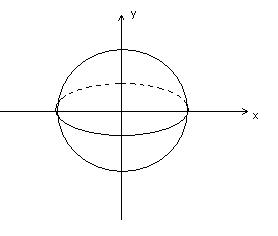
Общиее уравнение сферы 
Эллипсоид. Рассмотрим эллипсоид вращения 
вокург оси Oz , и будем пересекаеть его паралельными
плоскаостями z=h, то есть 
Так как левая часть неоатрицательна, то правая часть также должна быть
неотрицательной
т.е. мы получим в сечении эллипсы
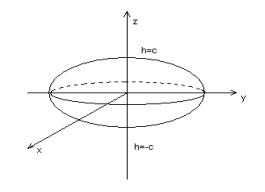
Таким образом, эллипсоид вращения можно
представить в виде параллельных концентрических окружности, наложенных на ось 
и края которых скользят по эллипсу
Параболоиды. Рассмотрим в плоскости 
параболу
;
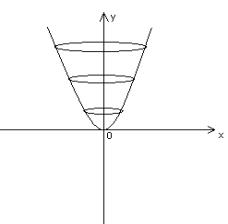
Будем вращать
параболу вокруг оси 
, получим параболоид вращения
Пересечем параболоид вращения плоскостью 
тогда в сечении получим окружности
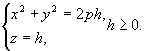
Параболоид вращения можно рассматривать как поверхность, образованную из концентрических окружностей
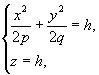
края которых скользят по параболе
Возьмем вместо окружностей концентрические эллипсы
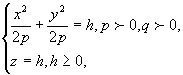
тогда, подставив вместо параметра 
переменную 
получим поверхность параболоида
Программа построения параболоида с анимацией на языке QBASIC [2]
10 PI =4*ATN (1): N=242: DIM PT (3, N) : SCREEN9,0: CLS : KEY
OFF
15 VIEW: WINDOW (-50,-50) – (-75, 75)
20 ' LINE (-20, 0) – (75, 0),
3, , &HAAAA
25 ' LINE (75, 0) - (-20, 0), 3,
, &HAAAA
BG = 60
AG = 30
26
IF BG = 360 TNEN BG = 0
REM IF AG =360 TNEN AG = 0
BG = BG +1
REM AG = AG + .5
L$ = "U"
L$ = INKEY$
IF L$ = "D" THEN BG = BG + . 5
IF L$ = "A" THEN
BG = BG - . 5
IF L$ = "W" THEN K = K+10:
IF L$ = "S" THEN K = K - 10:
IF L$ = "Q" THEN END
IF L$ = "E" THEN AG = AG + . 5
IF L$ = "F" THEN AG = AG - . 5
IF L$ = "T" THEN K1 = K1+10
IF L$ = "G" THEN K1 = K1-10
VIEW: WINDOW (-50 +K, -50 +K) – (5 +K1, 5 + K 1)
BN = PI * BG / 180: CB = COS (
BN ): SB = SIN (BN)
40 AN = ( PI * AG / 180): CA = COS (AN): SA = SIN (AN)
45 RESTORE
REM FOR I = 1 TO 3 : FOR J = 1
TO N: READ PI (I , J): NEXT: NEXT
POP = 0
OPEN "I" , #1, "S. TXT"
DO WHILE NOT EOF (1)
POP=POP +1
INPUT #1, PT (1, POP), PT (2, POP), PT (3, POP)
IF POP = N THEN GOTO 49
LOOP
49 CLOSE #1
50 FOR I =1 TO N
55 ZZ = PT ( 1,I) =PT (3, I) * CB-PT(1,I)* SB
60 PT (1, I) = PT (3, I) * SB+PT (1, I ) * CB
65 PT (3, I )= ZZ
70 YY= PT (2, I ) * CA –PT (3, I
)* SA
75 PT (3, I ) = PT (2, I ) * SA + PT (3, I ) * CA
80 PT (2, I ) = PT (2, I ) * SA +PT (3, I ) * CA
80 PT (2, I ) = YY: NEXT
PSET (PT(1, 1), (2 , 1)), 2
HH=0
ROR I = 2 TO 121
HH = HH +1
IF HH =11 THEN PSET (PT(1, I), PT (2 , I )), 2 ELSE LINE –(PT (1, I ) , PT (2, I )) ,
IF HH = 11 THEN HH =0
NEXT I
PSET (PT (1, 123 ), PT (2, 123)) , 2
HH = 0
FOR I = 124 TO 242
HH = HH +1
IF HH =11 THEN PSET (PT(1, I) ,
PT (2, I )), 2 ELSE LINE – (PT (1, I ),
PT(2,I)),
IF HH = 11 THEN HH = 0
NEXT I
LINE (PT (1, 242), PT (2,242 ))- (PT(1,121), PT(2,121)), 2
90 RESTORE:
REM FOR I=1 TO 3: ROR J=1 TO N: READ PT(I, J): NEXT: NEXT
POP=0
OPEN “I”,#1, “S.TXT”
DO WHILE NOT EOF(1)
POP=POP+1
INPUT #1, PT(1, POP), PT(2, POP), PT(3, POP)
IF POP=N THEN GOTO 94
LOOP
CLOSE #1
BN=PI*(BG) / 180:CB=COS(BN): SB=SIN(BN)
AN=(PI*(AG)/ 180): CA=COS(AN): SA=SIN(AN):
95 FOR I=1 TO N
100 ZZ = PT (3, I) * CB – PT ( 1, I) * CB
105 PT ( 1, I) = PT (3, I ) SB +
PT ( 1, I) * CB
110 PT (3, I) = ZZ
115 YY = PT (2, I ) * CA – PT (3, I) * SA
120 PT (3, I ) = PT (2, I) * SA + PT (3, I ) * CA
125 PT (2, I ) = YY : NEXT
130
PSET ( PT (1, 1), PT (2, 1)) ,
0
135
HH = 0
FOR I = 2 TO 121
HH = HH + 1
IF HH = 11 THEN PSET
( PT (1, I), PT (2, I), 0 ELSE LINE
-(1, I ), PT (2, I)), 0
IF HH = 11 THEN HH = 0
NEXT I
PSET ( PT(1, 123), PT (2, 123)),
0
HH = 0
FOR I = 124 TO 242
HH = HH+1
IF (HH = 11) THEN PSET ( PT (1, I ), PT (2, I
)), 0 ELSE LINE – (PT(1, I), PT ( 2, I)), 0
IF HH = 11 THEN HH = 0
NEXT I
LINE ((2 , 242 )) – (PT (1, 121)), PT (2, 121)) 0
150 LOCATE 25, 1: GOTO 26: INPUT "", A$: WIDTH 80: OUT 985, 10
: END
В среде Mathcad [3]
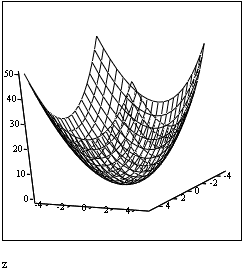
Список литературы
- К. Хасеинов. Каноны математики. –Алматы.: 2004. -250 с.
- Фаронов В. В. QBASIC 7.0. Начальный курс. Учебное пособие. – М. : Нолидж, 2001. –
576с.
- Дьяконов В. П. Энциклопедия MathCAD 2001 и MathCAD 11. – М.:
Солон Пресс, 2004. -831с.