Економічні науки/математика/диференційні та інтегральні рівняння

Журавльова А. В., Івахненко Н. М.

Донецький державний університет економіки і торгівлі імені М. Туган-Барановського, Україна

Застосування методів диференціального числення функцій багатьох змінних в економічних дослідженнях.

Важливими елементами мікро- й макроекономічної теорії раціонального господарювання є, з одного боку, виробник, який витрачає економічні ресурси для виготовлення товарів або надання послуг, а з іншого – виробничі технологічні процеси.

Вивчаючи економічні процеси в сучасному суспільстві для побудови економіко-математичної моделі, яка описує внутрішній бік виробництва, потрібно зібрати необхідну інформацію про фактори і ресурси, які впливають на обсяг продукції, що випускається.

Виробнича функція – це функція, незалежна змінна х якої набуває обсягу ресурсу, котрий використовується у виробництві (фактора виробництва), а залежна змінна у – значення обсягу продукції, котру випускає дане підприємство, фірма або галузь. Позначення виробничої функції: у=f(x). Тут х(х > 0) і у(у > 0) – числові величини, тобто у = f(x) є функцією однієї змінної х. У зв’язку з цим виробничу функцію називають одно ресурсною, або одно факторною. Її область визначення – множина невід’ємних дійсних чисел. Запис у = f(x) означає: якщо ресурс витрачається або використовується в кількості х одиниць, то продукція випускається в кількості у = f(x) одиниць. Знак функції f є характеристикою виробничої функції, яка перетворює ресурс у випуск продукції, і пов’язує між собою незалежну змінну х та залежну змінну у.

Аналіз виробництва здійснюють за допомогою теорії виробничих функцій.

Виробнича функція багатьох змінних – це функція, незалежні змінні х₁, х₂, ..., х_п якої набувають значень обсягів ресурсів, що використовуються у виробництві (число змінних n дорівнює числу ресурсів), а значення функції виражає обсяг випуску продукції:

y = f(x) = f(x₁, x₂, …? x_n).

Тут y(y>=0) – скалярна величина, а x – векторна; (х₁, х₂, ..., х_n) – координати вектора, тобто f(x₁, x₂, …, x_n) є числовою функцією n (багатьох) змінних (х₁, х₂, ..., х_n). Її називають багатофакторною виробничою функцією. За економічним змістом х₁>=0, …x₂>=0, …,x_n>=0. Отже, областю визначення багатофакторної виробничої функції є множина n-вимірювальних векторів х, усі координати яких – невід’ємні числа.

Для окремого підприємства виробнича функція f(x₁, x₂, …, x_n) може пов’язувати обсяг випуску продукції (в натуральному або вартісному вираженні) з витратами робочого часу за різними видами трудової діяльності, різноманітними видами сировини, енергії, основного капіталу тощо. Виробничі функції такого типу характеризують технологію підприємства.

Будуючи виробничу функцію для регіону або країни в цілому, за обсяг річного випуску у зазвичай беруть їхній сукупний продукт(доход); ресурси розглядають, як основний капітал (х₁=К – обсяг основного капіталу, що використовується протягом року) і працю (х₂=L – витрати праці, що використовуються протягом року). Таким чином, дістають двофакторну виробничу функцію y = f(x₁, x₂)= f (K, L), наприклад функцію Кобба-Дугласа.

Доходом R фірми за певний період часу (наприклад у певному році) називають добуток загального обсягу продукції q , що випускається, на (ринкову) ціну p₀ цієї продукції:

R= p₀q.

Витратами С фірми називають її загальні витрати за певний інтервал часу, тобто

C = p₁x₁ + p₂x₂ + …+ p_nx_n,

Де х₁, х₂, ..., х_п – обсяги ресурсів, які використовує фірма (фактори виробництва); р₁, р₂, ..., р_n – ринкові ціни на ці ресурси (фактори виробництва).

Прибутком Р фірми за певний інтервал часу називають різницю між одержаним нею доходом та витратами виробництва: Р = R – C, тобто

P(X₁, X₂, …, X_n) = p₀ f (x₁, x₂, …, x_n) – (p₁x₁ + p₂x₂ + …+ p_nx_n).

У теорії фірми вважають: якщо фірма функціонує в умовах чистої конкуренції, то на ринкові ціни p₀, p₁, p₂,...p_n вона вплинути не може, тобто фірма „погоджується” із цими цінами.

Основна задача багато ресурсної фірми полягає в тому, що фірма намагається одержати максимальний прибуток шляхом раціонального розподілу ресурсів, які використовуються у виробництві.

З математичного погляду ця задача зводиться до розв’язання зачачі про знаходження максимального значення функції прибутку P = P(x₁, x₂, …, xn), тобто функцію прибутку досліджують на екстремум і визначають при яких значеннях (х; х;..., х ) вона набуває свого найбільшого значення.

Набір ресурсів (х; х;..., х ), який забезпечує фірмі максимальний прибуток, називають оптимальним.

Фірма може вільно вибирати вектор ресурсів х = (x₁, x₂, …, x_n), причому x₁, і = 1,2, …, n. Знайдемо оптимальну для фірми комбінацію ресурсів (х; х;..., х ), тобто розв’яжемо основну задачу багаторесурсної фірми.

Прирівнявши частинні похідні функції прибутку до нуля, дістанемо

= , (1)

Припустимо, що всі витрати ресурсів строго додатні (нульові просто можна не розглядати). Тоді (х; х;...; х ), яка визначається співвідношеннями (1), є критичною, й вважатимемо, що умови, які накладаються на виробничу функцію, гарантують, що це точка максимуму. Тоді (х; х;...; х ) називають оптимальним розв’язком задачі багаторесурсної фірми.

Нехай задано виробничу функцію фірми f(x.y) = x та ринкові ціни продукції p умов. грош. од. Знайдемо комбінацію ресурсів (), за якої фірма одержить максимальний прибуток.

Функція прибутку фірми

Дослідимо її на екстремум. Запишемо необхідні умови існування локального екстремуму. Для цього знайдемо частинні похідні функції прибутку й прирівняємо їх до нуля:

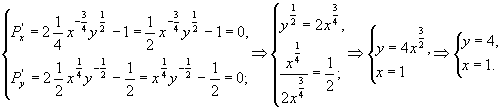
Отже, точка М(1;4) є критичною.

Перевіримо достатні умови. Для цього знайдемо частинні похідні другого порядку та обчислимо їхні значення в точці М(1;4):

Оскільки

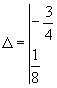
і

то точка М(1;4) – точка локального максимуму.

Обчислимо максимальний прибуток фірми:

Таким чином, в економіці дуже часто необхідно розв’язувати задачі на екстремум функції багатьох змінних, тому що економічні показники зазвичай залежать від багатьох факторів. Такі задачі добре вивчені теорією функцій багатьох змінних, яка використовує методи диференціального числення.

Список літератури:

1. М. В. Грищенко. Математика для економістів: Методи й моделі, приклади й задачі: Навч. Посібник. – К.: Либідь, 2007. – 720 с.

2. Математическая энциклопедия/ Гл. ред. И. М. Виноградов. – М.: Советская Энциклопедия. Т. 4 Ок – Сло. 1984.