Технические науки/10.Горное дело

Каражанов А.А.

Таразский государственный университет имени М.Х.Дулати,

Республика Казахстан

Теория квадратичных преобразований и геометрическое проектирование поверхностей подземных выработок

В данной статье излагаются основы теории моделирования двухполостного гиперболоида в виде (2-2)-значного точечного преобразования с вертикальной осью симметрии на совмещенной плоскости. Это преобразование обозначим символами Д₂.

Метод получения (2-2)-значного преобразования Д₂ заключается в следующем:

1) Отмечаем произвольную точку на поверхности заданного (2-2)-значного преобразования Q₂ с действительной осью ОУ (рис.1). Через точку проводим окружность К₂ на поверхности Q₂ (рис.2).

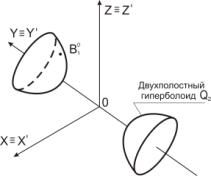
Рис.1 Отображаемая поверхность Q₂

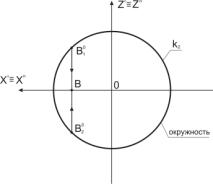
Рис.2 Построение точки В

2) Точку ортогонально проецируем на плоскость П₂ (ХОУ), получим точку В. На рис.2 точка В построена на плоскости окружности К₂. На поверхности Q₂ расположена еще одна точка , которая проецируется в точку В.

3) Поверхность Q₂ вращаем на 90⁰ вокруг оси ОУ так, чтобы положительное направление оси ОZ совпадало с отрицательным направлением оси ОХ. Получим новую поверхность . При этом точки и описывают окружность К₂ (рис.3). После этого точки и занимают новые положения и (рис.3).

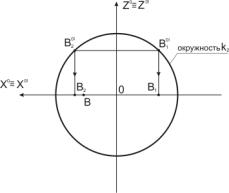
Рис.3 Построение точек В₁ и В₂

4) Точки и ортогонально проецировав на плоскость , получим точки В₁ и В₂. Таким образом, точке В соответствуют две точки В₁ и В₂ на совмещенной плоскости ≡(рис.4). Другими словами, на совмещенной плоскости установлено (1-2)-значное точечное преобразование. Это преобразование, обозначенное символами Д₂, отображает каждую точку плоскости П₂ в две точки плоскости .

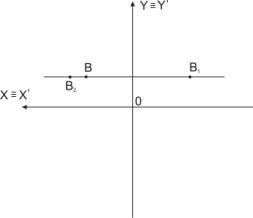
Рис.4 Изображение точек В, В₁ и В₂ на плоскости ≡

В обратном направлении каждая точка В₁ плоскости отображается в две точки и плоскости П₂, одна из которых инцидентна точкой В. Это отображение обозначено символами .

Уравнение (1-2)-значного преобразования определяется следующим образом:

1. Уравнение поверхности Q₂ записывается в виде:

(1)

где R – параметр поверхности Q₂.

2. Вращение точки вокруг оси ОУ на 90⁰, рассмотренное выше, можно записать в виде

(2)

3. Значение z из соотношения (2) подставив в уравнение (1), получим:

(3)

4. Осью преобразования Д₂ является ось ОУ, поэтому запишем

(4).

5. Уравнения (3) и (4) обьединив в одну систему, получим уравнения преобразования Д₂ в виде

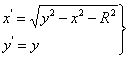(5)

где ,- координаты точки-образа;

x, y – координаты точки-прообраза;

R – параметр преобразования, R>0.

6. Из системы уравнении (5) можно определить уравнения обратного преобразования в виде:

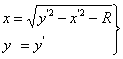(6)

где ,- координаты точки-образа;

x, y – координаты точки-прообраза;

R – параметр преобразования.

Графическая модель преобразования Д₂ определяется следующим образом:

1. Запишем уравнения преобразования Д₂:

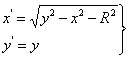(7)

где ,- координаты точки-образа;

x, y – координаты точки-прообраза;

R – параметр преобразования;

2. Первое уравнение системы (7) преобразует точку В (x,y) в две точки В₁ и В₂ с абсциссами:

(8)

(9)

Второе уравнение системы (7) показывает, что точки В₁ и В₂ расположены симметрично относительно оси ОУ;

3. Значение выражения графически определяется следующим образом:

3.1. сумму обозначим в виде

(10)

3.2. выражению (10) соответствует на чертеже прямоугольный треугольник 013 (рис.5), где катет 01 равен х, катет 13 равен R, гипотенуза равна е. Для построения треугольника 013 из заданной точки В опускаем перпендикуляр к оси ОХ (до точки 1) и из точки 2 проводим горизонтальную прямую до точки 3;

3.3. учитывая выражение (10), перепишем первое уравнение системы (7) в виде:

или

(11)

3.4. выражению (11) соответствует на чертеже прямоугольный треугольник 046 (рис.5), где катет 04 равен е, гипотенуза 06 равна у, катет 46 равен искомой ;

3.5. из точки 6 проводим вертикальную прямую и из точки В проводим горизонтальную прямую, которые пересекаются в точке В₁ с координатами (,). Точка В₂ строится симметрично точке В₁ относительно оси ОУ.

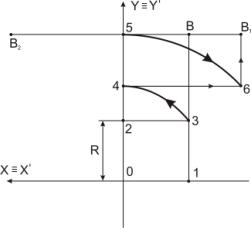
Рис.5 Построение графической модели преобразования Д₂

Таким образом рис.5 представляет собой графическую модель преобразования Д₂.

Область определения преобразования Д₂ определяется следующим образом:

1) правую часть первого уравнения системы (5) приравниваем к нулю:

(12)

2) анализ уравнения (12) показывает, что должно быть или

(13)

3) уравнение на плоскости изображает множество точек, расположенное выше или ниже двух ветвей гиперболы q с мнимой осью ОХ (заштрихованная область на рис.6). Эта область представляет собой областью определения преобразования Д₂.

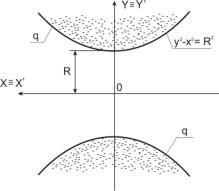
Рис.6 Область существования преобразования Д₂

Литература

1. Джапаридзе И.С. Геометрические преобразования пространства и их применения в начертательной геометрии. Методы начертательной геометрии и ее приложения. – М.:1955 – 54-222 с.

2. Ермаков А.В. Кремоновы преобразования пространства в конструировании рациональных каркасных поверхностей: автореф. ...канд.техн.наук: 05.01.01. – М.: МТИПП, 1977 – 17 с.

3. Завьялов Ю.С.,Леус В.А., Скороспелов В.А. Сплайны в инженерной геометрии. - М.: Машиностроение, 1985 – 222 с.

4. Конакбаев К.К. Конструирование обводов из дуг уникурсальных циркулярных кривых посредством кремоновых инволюций. автореф. ...канд.техн.наук: 05.150. – М.: МТИПП, 1972 – 18 с.

5. Котов И.И. Алгоритмы конструирования каркасных поверхностей. – М.: МАИ, 1975.