Математика/1. Дифференциальные и интегральные
уравнения
Докторант PhD, к.ф.-м.н. Оспанова А.Б.
Евразийский
национальный университет им. Л. Н. Гумилева, Казахстан
Об устойчивости одной приближенной
схемы для сингулярной задачи Коши
В работе
рассматривается одна модель приближенной схемы (разностной схемы) для
численного решения задачи Коши дифференциального уравнения первого порядка с
сингулярностью на бесконечности.
Пусть дана краевая
задача Коши
![]() (1)
(1)
где ![]() – непрерывная в
– непрерывная в ![]() функция такая, что
функция такая, что ![]() для всех
для всех ![]() и
и
![]() (2)
(2)
Целью настоящей работы
является построение приближенной схемы для численного решения уравнения (1). Следующие
определения взяты из [1].
Пусть ![]() ,
, ![]() – банаховы
пространства,
– банаховы
пространства, ![]() – пространство всех
непрерывных линейных операторов, действующих из
– пространство всех
непрерывных линейных операторов, действующих из ![]() в
в ![]() . Пусть
. Пусть ![]() – оператор из
– оператор из ![]() в
в ![]() .
.
Приближенной
схемой уравнения
![]() (3)
(3)
называют
последовательность уравнений
![]() (4)
(4)
где ![]() ,
, ![]() (
(![]() ) – банаховы пространства, связанные с
) – банаховы пространства, связанные с ![]() (
(![]() ) посредством операторов
) посредством операторов ![]() (
(![]() ).
).
Через ![]() (
(![]() ) будет обозначаться область определения оператора
) будет обозначаться область определения оператора ![]() (
(![]() ).
).
Существенное значение в
сходимости приближенной схемы (4) имеет свойство устойчивости данной схемы.
Будем
говорить, что приближенная схема (4) устойчива, если существуют постоянная ![]() и
целое
и
целое ![]() такие,
что
такие,
что
![]() (5)
(5)
Ниже через ![]() ,
, ![]() будут обозначаться
пространство непрерывных на
будут обозначаться
пространство непрерывных на ![]() функций
функций ![]() таких, что
таких, что
![]()
пространство функций ![]() , имеющих в
, имеющих в ![]() непрерывную
производную
непрерывную
производную ![]() . В
. В ![]() зададим норму
зададим норму
![]()
Пусть ![]() – пространство Лебега
с нормой
– пространство Лебега
с нормой
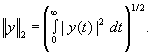
Пусть ![]() – пространство всех
– пространство всех ![]() , имеющих в
, имеющих в ![]() абсолютно непрерывную
производную
абсолютно непрерывную
производную ![]() и таких, что
и таких, что
![]()
Обозначим через ![]() пополнение
пополнение ![]() по норме
по норме ![]() . Уравнение (1) запишем в операторной форме (3), где возьмем
. Уравнение (1) запишем в операторной форме (3), где возьмем
![]() (6)
(6)
Оператор ![]() в (6) рассматриваем
как оператор из
в (6) рассматриваем
как оператор из ![]() в
в ![]() , где
, где ![]() . Норма в
. Норма в ![]() (
(![]() )
)
![]()
Область определения ![]() .
.
Построение
приближенной схемы
Нетрудно показать, что ![]() удовлетворяет условию
удовлетворяет условию
![]()
В силу этого следующая функция Отелбаева
![]()
конечна, а ![]() – непрерывная,
положительная и ограниченная на
– непрерывная,
положительная и ограниченная на ![]() функция. Имеет место
характеристическое равенство
функция. Имеет место
характеристическое равенство
![]() (7)
(7)
См. [2]. Положим ![]() . Возьмем некоторое достаточно малое
. Возьмем некоторое достаточно малое ![]() и пусть
и пусть
![]()
Устроим дизъюнктное покрытие отрезка ![]() промежутками
промежутками ![]()
![]() , где
, где ![]()
![]() ,
, ![]() . Для этого возьмем целые
. Для этого возьмем целые ![]() ,
, ![]() такие, что
такие, что ![]() . Каждому
. Каждому ![]() соотнесем равномерную
сетку
соотнесем равномерную
сетку ![]() ,
, ![]() ,
, ![]() ,
, ![]() , (
, (![]() ). Пусть
). Пусть ![]() (
(![]() ). Мы будем привлекать векторные арифметические пространства
). Мы будем привлекать векторные арифметические пространства ![]() ,
, ![]() ,
, ![]() с нормами
с нормами
![]()
![]()
соответственно
![]()
Пусть ![]() . Норма
. Норма
![]()
Для ![]() положим
положим
![]()
Далее, пусть ![]() с нормой
с нормой
![]()
Для ![]() положим
положим
![]()
Пусть ![]() ,
, ![]() ,
, ![]() – операторы, заданные
равенствами
– операторы, заданные
равенствами
![]() (8)
(8)
где
![]()
![]()
![]() (9)
(9)
где
![]() (10)
(10)
![]() (11)
(11)
![]() (12)
(12)
О
свойствах приближенной схемы
Будем
говорить, что функция ![]() удовлетворяет
условию медленного изменения (относительно характеристического размера
удовлетворяет
условию медленного изменения (относительно характеристического размера ![]() ), если существуют такие
), если существуют такие ![]() , что
, что
(![]() )
) ![]() как только
как только ![]() .
.
с абсолютной постоянной ![]() . См. [3].
. См. [3].
Будем
говорить, что ![]() вложено
в
вложено
в ![]() , если
, если ![]() и
и
![]() для
всех
для
всех ![]() .
.
Утверждение. А) Пусть ![]() удовлетворяет условию
(
удовлетворяет условию
(![]() ). Тогда
). Тогда ![]() .
.
Б) Пусть ![]() удовлетворяет условию
(
удовлетворяет условию
(![]() ). Тогда
). Тогда ![]() вложено в
вложено в ![]() .
.
В) Оператор ![]() .
.
Г) Оператор ![]() .
.
Здесь использованы известные неравенства
(вложения Соболева):
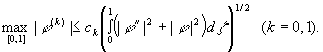 (13)
(13)
Теорема. Пусть выполнено условие (![]() ) и пусть
) и пусть ![]() – оператор, заданный
равенствами (9)-(12). Тогда приближенная схема (4) с правой частью
– оператор, заданный
равенствами (9)-(12). Тогда приближенная схема (4) с правой частью ![]() устойчива.
устойчива.
Литература:
1. Треногин В.А.
Функциональный анализ. – 3-е изд. – М.: ФИЗМАТЛИТ, 2002. – 488 с.
2. Отелбаев М.,
Кусаинова Л. К. Оценки спектра одного класса дифференциальных операторов //
Збірник праць Інституту математики НАН України Теорія операторів,
диференціальні рівняння і теорія функцій. – Київ, 2009. – Т. 6. – № 1. – С.
165-190.
3. Соболев С. Л. Некоторые
применения функционального анализа в математической физике. – 3-е изд. – М.:
Наука, 1988. – 336 с.