К.т.н Боранкулова
Г.С.
(Таразский
государственный университет им.М.Х.Дулати, Казахстан)
РЕШЕНИЕ
ЭКОНОМИЧЕСКИХ ЗАДАЧ СРЕДСТВАМИ ТАБЛИЧНОГО ПРОЦЕССОРА
Всем хорошо известна
востребованность экономических знаний сегодня. Самостоятельность в принятии
решений, эффективный анализ проблемы, отстаивание собственной точки зрения –
эти качества приобретёт каждый, работая в одной команде над решением
экономической задачи.
Для решения тех или иных
экономических задач хорошо было бы использовать различные высокотехнологичные
компьютерные программы. К сожалению, для многих современных организаций это не
представляется возможным, так как у каждой из них существует свой ряд
особенностей производства, а разработка таких программ для каждого предприятия
в отдельности повлечет за собой большие материальные затраты.
В
своей работе я хотела бы наглядно продемонстрировать, что для индивидуального
предпринимателя или небольшой фирмы хорошей альтернативой специализированным программам может оказаться использование обычного
табличного процессора MS Excel, в
котором есть все необходимые средства и возможности для выполнения экономических, производственных,
оптимизационных расчетов. С помощью MS Excel каждая организация сможет
решать такие задачи, во-первых, экономя массу времени, а, во-вторых, сохраняя
свой бюджет. Именно индивидуальный подход к решению достаточно
сложных задач и наличие надежных алгоритмов позволяют получить решение быстро и эффективно.
Цель работы – убедиться в том,
что табличный процессор MS Excel
является мощным средством при решении задач оптимизации.
Задача работы – определить,
какими должны быть оклады сотрудников фирмы, при условии, что оклад курьера не
должен быть меньше 14000 с помощью табличного процессора MS Excel на конкретном примере.
Постановка задачи:
Пусть
известно, что для нормальной работы фирмы требуется 5…7 курьеров, 8…10 младших
менеджеров, 10 менеджеров, 3 заведующих отделами, главный бухгалтер,
программист, системный аналитик, генеральный директор фирмы.
Общий
месячный фонд зарплаты должен быть минимален.
В
качестве модели решения этой задачи возьмем линейную модель.
Тогда
условие задачи имеет вид:
N1*A1*х+N2*(A2*х+B2)+...+N8*(A8*х+B8)
= Минимум,
· где Ni -
количество работников данной специальности;
· х - зарплата
курьера;
· А i и Вi -
коэффициенты заработной платы сотрудников фирмы.
Выполнение задания:
1. Создать файл
«Штатное расписание».
2. В меню Сервис активизировать команду Поиск решения (Сервис/ Надстройки/
Поиск решения).
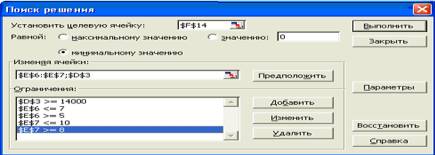
3. В окне Установить целевую ячейку указать
ячейку F14, содержащую модель – суммарный фонд заработной платы. Поскольку
необходимо минимизировать общий месячный фонд зарплаты, необходимо
активизировать кнопку равной - Минимальному
значению.
4. В окне Изменяя ячейки указать адреса
ячеек, в которых будет отражено количество курьеров и младших менеджеров, а
также зарплата курьера - $E$6:$E$7;$D$3 (при задании ячеек Е6, Е7 и D3
необходимо держать нажатой клавишу [Ctrl]).
5. Используя
кнопку Добавить в
окнах Поиск решения и Добавление ограничений, описать
все ограничения задачи:
·
количество курьеров изменяется от 5 до 7,
·
младших менеджеров от 8 до 10,
·
зарплата курьера>14000.
6. Ограничения
набрать в виде:
$D$3
>= 1400; $E$6 >= 5; $E$6 <= 7; $E$7 >= 8; $E$7 <= 10
7. Активизировать
кнопку Параметры и введите
параметры поиска.
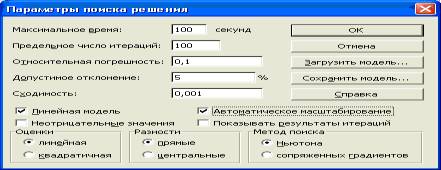
8. Запустить
процесс поиска решения нажатием кнопки Выполнить в окне Поиск решения.
На экране отобразится окно Результаты
поиска решения.
9. В
открывшемся диалоговом окне Результаты
поиска решения задать опцию Сохранить найденное решение.
В ходе
выполнения данной работы я неоднократно убедилась в том, что табличный
процессор MS Excel имеет все необходимые
средства для выполнения экономических, производственных и оптимизационных
расчетов и экономит массу времени.
Представленные
в данной работе решения задачи с помощью MS Excel
напрямую доказывают это.
Литература
1.
Практикум по экономической информатике: Учебное пособие. Часть 1. /Под ред.
Шуремова Е.Л., Тимаковой Н.А., Мамонтовой Е.А. – М.: Изд-во «Перспектива»,
2000.
2. Карлберг К. Бизнес-анализ с помощью Excel /
Пер.с англ.:- М.: Издательский дом «Вильямс», 2001.