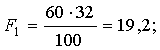Современные информационные технологии/ 2. Вычислительная техника и программирование

К.т.н. Харченко Є.М., к.т.н. Самарець Н.М.

Дніпропетровський державний агроуніверситет, Україна

Статистичні методи перевірки гіпотез в ентомології

з використанням MS Excel

При постановці дослідження досить часто виникає питання про розходження груп спостережень. Його вирішення зводиться до порівняння статистичних характеристик, що оцінюють параметри законів розподілу, тобто до перевірки статистичних гіпотез. Статистична гіпотеза – це наукове припущення про ті чи інші статистичні закони розподілу розглянутих випадкових величин, що може бути перевірене на основі вибірки. Майже завжди задача полягає в перевірці нульової гіпотези Н_о – про відсутність реального розходження між фактичними і теоретичними показниками. Якщо розходження близькі до нуля чи знаходяться в області припустимих значень, то нульова гіпотеза приймається. Якщо ж розходження виявляються в критичній для даного статистичного критерію області, неможливі при нашій гіпотезі і тому несумісні з нею, то Н_о відкидається. Прийняття гіпотези означає, що дані не суперечать припущенню про відсутність розходжень між фактичними і теоретичними чи двома рядами фактичних розподілів. Відкидання гіпотези означає, що емпіричні дані несумісні з Н_о та вірна інша, альтернативна гіпотеза. Справедливість Н_о перевіряється обчисленням статистичних критеріїв перевірки для визначеного рівня значимості.

Критерій хі-квадрат (c²) застосовують, коли необхідно встановити відповідність двох порівнюваних рядів розподілу – емпіричного і теоретичного чи двох емпіричних. Критерій c² представляє суму квадратів відхилень емпіричних частот f від теоретичних F, віднесену до теоретичних частот: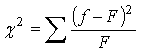. Цей показник використовується при вивченні якісних ознак для оцінки відповідності емпіричних даних теоретичній передумові, нульовій гіпотезі H₀. Гіпотеза відкидається, якщо , і не відкидається, якщо ; коли фактичні та теоретичні очікувані частоти збігаються, c²=0. Граничні значення c², при яких H₀ приймається, приведені в довідкових таблицях. Величина c² залежить від числа ступенів волі. У найбільш типових випадках число ступенів волі визначається по формулі , де с- число рядків, K – число стовпчиків в аналітичній таблиці.

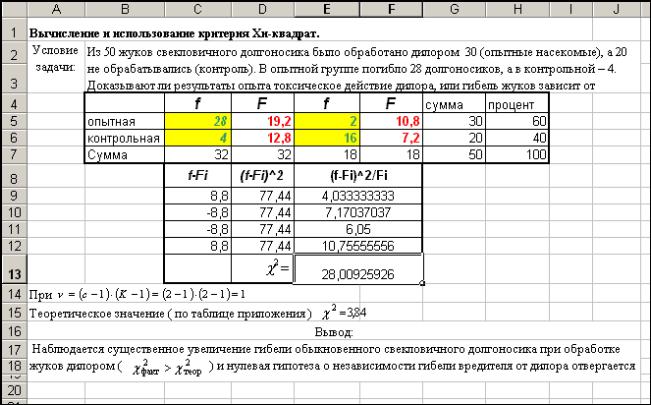
Приклад із агрономії. З 50 жуків бурячного довгоносика було оброблено дилором 30 комах (дослідна група), а 20 не оброблялися (контрольна група). У дослідній групі загинуло 28 довгоносиків, а в контрольній – 4. Необхідно з’ясувати, чи доводять результати досвіду токсичну дію ділора, або загибель жуків залежить від випадкових причин.

У таблиці приведені обчислені очікувані кількості комах по групах, де f і F – відповідно фактично спостережена та теоретично очікувана кількості.

Група комах	кількість комах				å	%
	загиблі		здорові
	f	F	f	F
Дослідна	28	19,2(F1)	2	10,8(F2)	30	60
Контрольна	4	12,8(F3)	16	7,2(F4)	20	40
å	32	32	18	18	50	100
%	64	-	36	-	-	100

Кількість комах по групах розподілилась таким чином:

загиблих в основній групі
здорових у дослідній групі
загиблих у контрольній групі
здорових у контрольній групі

Розходження між фактичними та очікуваними кількостями комах у групах:

	f-Fi	(f-Fi)^2
f-F1	8,8	77,44	4,04
f-F2	-8,8	77,44	7,17
f-F3	-8,8	77,44	6,05
f-F4	8,8	77,44	10,75
c^2=			28,0

При теоретичне значення .

Таким чином, можна зробити висновок, що спостерігається істотне збільшення загибелі звичайного бурячного довгоносика при обробці жуків ділором (), і нульова гіпотеза про незалежність загибелі шкідника від ділора відкидається.

Для рішення задачі застосовано електронні таблиці Excel Microsoft Office. На рисунку наведена умова задачі, розміщення даних та результати обчислень.