Математика / 5. Математическое моделирование

к.ф.-м. н. Калжанов М.У.

Костанайский государственный университет

имени А.Байтурсынова

Дискриминантный анализ идентификации объектов двух переменных

Дискриминантный анализ – это совокупность методов, позволяющих решать задачи идентификации объектов по заданному набору характерных признаков.

Процесс разработки дискриминантного анализа можно разбить на два этапа и каждый из них можно рассматривать как совершенно самостоятельный метод.

Первый этап – определение и формальное описание различий между существующими множествами (группами) наблюдаемых объектов.

Второй этап – непосредственная классификация новых объектов, т.е. отнесение каждого объекта к одному из существующих множеств.

Пусть имеется множество единиц наблюдения, каждая из которых характеризуется несколькими признаками (переменными): – значения j-й переменной у i-го объекта ; .

Предположим, что все множество объектов разбито на несколько подмножеств (два и более). Из каждого подмножества взята выборка объемом , где – номер подмножества (класса) .

Признаки, которые используются для того, чтобы отличать одно подмножество от другого, называются дискриминантными переменными.

Число дискриминантных переменных не ограничено, но на практике выбор должен осуществляться на основании логического анализа исходной информации. Число объектов наблюдения должно превышать число дискриминантных переменных, т.е. . Предполагается, что дискриминантные переменные – линейно независимые нормально распределенные многомерные величины.

Рассмотрим случай для двух дискриминантных переменных. Функция называется канонической дискриминантной функцией, а величины и – дискриминантными переменными

. (1.1)

Дискриминантная функция может быть как линейной, так и нелинейной. Выбор вида этой функции зависит от геометрического расположения разделяемых классов в пространстве дискриминантных переменных.

Коэффициенты дискриминантной функции () определяются таким образом, чтобы и как можно больше отличались между собой.

Вектор коэффициентов дискриминантной функции () определяется по формуле

. (1.2)

Полученные значения коэффициентов подставляют в формулу (1.1) и для каждого объекта в обоих множествах вычисляют дискриминантные функции , затем находят среднее значение для каждой группы (). Таким образом, каждому -му наблюдению, которое первоначально описывалось -переменными, будет соответствовать одно значение дискриминантной функции, и размерность признакового пространства снижается.

Классификация при наличии двух обучающих выборок. Перед тем как приступить непосредственно к процедуре классификации, нужно определить границу, разделяющую два множества. Такой величиной может быть значение функции, равноудаленное от и , т.е.

. (1.3)

Величина с называется константой дискриминации.

Объекты, расположенные над разделяющей поверхностью находятся ближе к центру множества , следовательно, могут быть отнесены к первой группе, а объекты, расположенные ниже этой поверхности, ближе к центру второго множества, т.е. относятся ко второй группе. Если граница между группами будет выбрана как сказано выше, то в этом случае суммарная вероятность ошибочной классификации будет минимальной.

Классификация при наличии -обучающих выборок. Рассмотрим особенности классификации объектов, возникающие при наличии -обучающих выборок (>2). Как и в случае с двумя обучающими выборками, предполагается, что каждое множество является нормально распределенным с различными векторами средних значений. Оценка совместной ковариационной матрицы рассчитывается по следующей формуле:

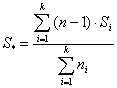, (1.4)

где – количество обучающих выборок; – матрица ковариации для i-й выборки; – численность i-й выборки.

В этом случае каждому множеству ставится в соответствие своя дискриминантная функция вида

.

Вектор коэффициентов этой функции () рассчитывается по формуле , а свободный член .

Новый классифицируемый объект с переменными будет отнесен к тому множеству , для которого величина будет максимальной.

Литература :

1. Дуброва Т.А., Бажин А.Г., Бакуменко Л.П. Методы многомерной

классификации. Дискриминантный анализ в системе STATISTICA. Учебное пособие / МГУ экономики, статистики и информатики; М., 2002.

2. Дубров А.М., Мхитарян В.С., Трошин Л.И. Многомерные статистические

методы: Учебник. – М.: Финансы и статистика, 2000.