Математика / 5. Математическое моделирование

к.ф.-м. н. Калжанов М.У.

Костанайский государственный университет

имени А.Байтурсынова

Алгоритм проверки гипотезы о равенстве вектора средних значений заданному вектору

Для проверки выдвигаемых гипотез используют статистические критерии, позволяющие определить, следует ли принять или опровергнуть нулевую гипотезу. Если расчетное значение критерия не превышает критического, то есть веские основания для принятия прямой (нулевой) гипотезы. В противоположном случае целесообразно предположить справедливость альтернативной гипотезы ().

Проверка статистических гипотез всегда допускает определенную вероятность ошибки в выводах:

- вероятность отвергнуть нулевую гипотезу, когда она справедлива;

- вероятность принять нулевую гипотезу, когда она ложна.

В исследованиях обычно используется - вероятность ошибки первого рода. Наиболее распространенными в практике экономического анализа значениями являются: 0,01; 0,05; 0,1.

В многомерном статистическом анализе проверка гипотезы о равенстве вектора средних значений заданному вектору основывается на тех же подходах, что и для одномерных величин. Но в этом случае имеет место -чисел выборочных средних значений: . Вектор сравнивается с постоянным вектором . Прямая гипотеза имеет вид

, при альтернативной .

Для проверки многомерной гипотезы данного вида используется критерий, известный как критерий Хотеллинга

, (1.1)

где - ковариационная матрица; - матрица с центрированными значениями переменной: .

Расчетное значение сравнивается с критическим значением, исчисляемым при заданном уровне вероятности () и числе степеней свободы и

. (1.2)

В формуле (1.2) - табличное значение F-критерия Фишера для числа степеней свободы и .

Многомерная гипотеза о равенстве вектора средних величин заданному вектору подтверждается при .

Пример 1. Для предприятия розничной торговля в административном районе установлены следующие нормативные показатели эффективности деятельности – 20 % и средняя продолжительность оборота оборотных средств – 12 дней. Предположим, что более низкие значения уровня рентабельности и скорости оборота означают нарушение ритмичности товарно-денежных операций и снижение конкурентоспособности предприятий торговли.

С целью оперативного контроля проведен анализ эффективности деятельности предприятия и получены следующие данные (таблица 1).

Таблица 1. Рентабельность средств предприятий

Номер объекта	Рентабельность, %	Продолжительность оборота, дней
01 02 03 04 05 06 07 08 09 10 11 12	14 12 16 14 15 18 22 20 13 19 12 14	19 15 19 17 24 12 10 15 18 20 22 23
Среднее значение ()	15,8	17,8

Оценим существенность различий между фактическими значениями рассматриваемых показателей и установленными нормативами. Уровень значимости зададим равным 0,05.

Решение. Определим следующие параметры многомерной случайной величины:

вектор средних значений ;

ковариационная матрица

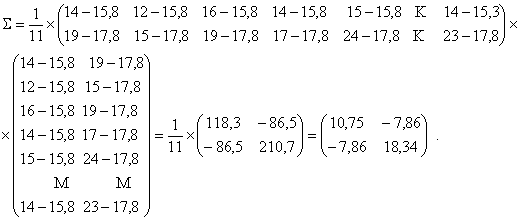
Обратная ковариационная матрица будет равна

.

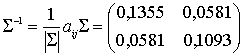Рассчитаем фактическое значение - критерия Хотеллинга

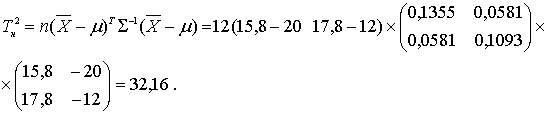
Критическое значение для заданного уровня значимости =0,05 составит

.

Как видно , расчетное значение - критерия почти в три раза превосходит критическое (32,16>9,8), что показывает расхождения между фактическими и нормативными значениями показателей.

Литература :

1. Айвазян С.А., Бежаева З.И., Староверов О.В. Классификация многомерных

наблюдений. – М.:Статистика, 1974. – 240 с.

2. Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы

эконометрики. – М.:ЮНИТИ, 1998.